ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Priyadharshini.J1, Akila Devi.S2, Askerunisa.A3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Clustering on Distribution measurement is an essential task in mining methodology. The previous methods extend traditional partitioning based clustering methods like k-means and density based clustering methods like DBSCAN rely on geometric measurements between objects. The probability distributions have not been considered in measuring distance similarity between objects. In this paper, objects are systematically modeled in discrete domains and the Kullback-Leibler Divergence is used to measure similarity between the probabilities of discrete values and integrate it into partitioning and density based clustering methods to cluster objects. Finally the resultant execution time and Noise Point Detection is calculated and it is compared for Partitioning Based Clustering Algorithm and Density Based Clustering Algorithm. The Partitioning and Density Based clustering using KL divergence have reduced the execution time to 68 sec and 22 Noise Points are detected. The efficiency of Distribution based measurement clustering is better than the Distance based measurement clustering.
Index Terms |
| Partitioning based clustering methods, Density based clustering method, Distribution based clustering, Kullback-Leibler divergence |
INTRODUCTION |
| Clustering is a grouping of similar objects based on their distance similarity measurement which is an “unsupervised classification”. Finding groups of objects such that the objects in a group will be similar to one another and different from the objects in other groups is called clustering. Basically clustering is categorized as inter cluster and intra cluster. The rule behind the cluster is “similarity between intra clustering is higher than the similarity between the inter clustering”. In this paper, Distance Based Clustering Algorithms like Partitioning Based and Density Based are used and various Distribution based measurements are applied. In the Partitioning Based Clustering approach, the k-means method uses the distance to measure the similarity between two objects. In the Density Based Clustering approach, the objects in geometrically dense regions are grouped together as clusters and clusters are separated by sparse regions. The above Distance based approaches cannot distinguish the two sets of objects having different distributions. Hence Kullback-Leibler divergence measurement is used. In the Kullback-Leibler divergence, the objects Probability Mass Functions (PMF) over the entire data space are different and the difference between the PMF’s can be captured using KL divergence. |
LIMITATIONS OF EXISTING SYSTEM |
| In the Partitioning clustering approach, [2], [4], [6], [7], [9] which is an extension of the k-means method, the expected distance to measure the similarity between two objects, an object P and a cluster center C (which is a certain point) is calculated using equation 1 |
 |
| Where P-Object, Var(P)-variance of P and The distance measure dist is the square of Euclidean distance. |
| Here, only the centers of objects are taken into account in certain versions of the k-means method. As every object has the same center, the expected distance based approaches cannot distinguish the two sets of objects having different distributions. |
| In the Density based clustering approach, [1], [3], [10], [18], [19] the basic idea behind the algorithms does not change objects in geometrically dense regions are grouped together as clusters and clusters are separated by sparse regions. Generally the objects are heavily overlapped. There is no clear sparse region to separate objects into clusters. Therefore, the density based approach cannot separate the objects. |
RELATED WORK |
| The Related work for the proposed paper comprises of the works that uses various clustering algorithms to implement the clustering of objects using Distribution measurement. |
| Alie.J et.al, [1] have used DBSCAN technique for clustering the spatial databases to identify arbitrary shape objects and to remove the noise during the clustering process. |
| Liping Jing.,et.al, [7] have used k-means Algorithm for clustering high dimensional objects in subspace. In high dimensional data, clusters of objects often exist in subspaces rather than in the entire space. The k-means clustering process uses the weight values calculated to identify the subsets of important dimensions that categorize clusters. |
| Grigorious,F,.Tzortzis, et.al, [8] have used Kernel K means Algorithm which was an extension of K means that depends on cluster initialization. |
PROPOSED SYSTEM |
| The difference between the distributions cannot be captured by geometric distances. In this paper, the Kullback-Leibler divergence is used to analyze the Probability Mass Functions (PMF) over the entire data space. The difference in the PMF value is captured by KL divergence. In general, KL divergence between two probability distributions is defined as follows. In the discrete case, let f and g are two probability mass functions in a discrete domain D with a finite number of values. The Kullback-Leibler Divergence between f and g is calculated using equation 2. |
 |
| Where f(x) and g(x) – Probability Mass Function. |
| The probability of discrete values is integrated with Partitioning and Density Based Clustering Methods to cluster objects. |
| A. System Model |
| Discrete values in the dataset are preprocessed and the values are supplied to the Partitioning and Density Based Algorithm and their corresponding results are evaluated. The Probability Mass Function (PMF) value is calculated to calculating KL divergence measurement. |
| Finally the values are again fed back to the Distance based algorithm and the results are compared. |
| 1) Data Preprocessing |
| Real world databases are highly susceptible to noisy, missing, and inconsistent data due to their typically huge size and their origin from multiple, heterogeneous sources. Low quality data will lead to low quality mining results so the preprocessing techniques are used to improve the quality. |
| In this paper, Data Cleaning is applied to remove the noise in the weather dataset. The Kullback- Leibler Divergence supports only the positive attribute values in the weather dataset so the negative attribute values are considered as a noise and it has removed from the weather dataset. |
 |
| Figure 1 describes how the Distance Based Clustering Algorithm like Partitioning and Density Based Clustering Algorithm works with the Distribution measurement of KL divergence. |
| 2) Measurement of Kullback-Leibler Divergence for Partitioning |
| Based Clustering Approach |
| The Kullback-Leibler Divergence (KL divergence for short) also known as Information entropy or Relative entropy. In the discrete case, let f and g are two probability mass functions in a discrete domain D with a finite number of values. The Kullback-Leibler divergence between f and g is calculated using (2) specified in proposed system. |
| The Kullback-Leibler divergence is used to measure similarity between the probabilities of discrete values. The Partitioning based clustering [18], [19], [20], [21], [22], [24] is calculated using (1). Finally, the KL divergence value is then integrated with the Partitioning based clustering approach. |
| 3) Measurement of Kullback-Leibler Divergence for Density |
| Based Clustering Approach |
| Density Based Spatial Clustering of Applications with Noise (DBSCAN) Algorithm [11], [12] ,13], [14], [16], [17], [25] locates regions of high density that are separated from the regions of low density. DBSCAN is a center based approach for clustering in which density is estimated for a particular point in the dataset by counting the number of points within the specified radius, r, of that point. |
| The center based approach consists of points such as, Core points- These points are in the interior of the dense region. Border points- These points are not the core points, but fall within the neighborhood of the core point. Noise points- A noise point is a point that is neither a core point nor a border point. |
 ' ' |
| DBSCAN ALGORITHM: |
| Input: The dataset D |
| Parameter: |
| Σ Neighborhood – Objects within a radius of r from an object. |
| Minpts - Minimum number of objects within the radius r. |
| Output: Region of high density is separated from region of low density. |
| Method: |
| If p>= minpts within the radius r |
| The point p is a core point |
| Else if p<minpts or p=neighborhood (core point) |
| The point p is a border point |
| Else |
| The point p is a noise point. |
| The Kullback-Leibler divergence between f and g is calculated using (2) and the value of KL divergence is then integrated with the density based clustering approach. |
| 4) PERFORMANCE METRICS |
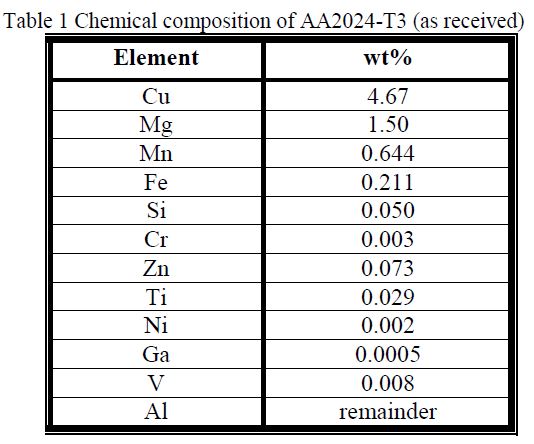
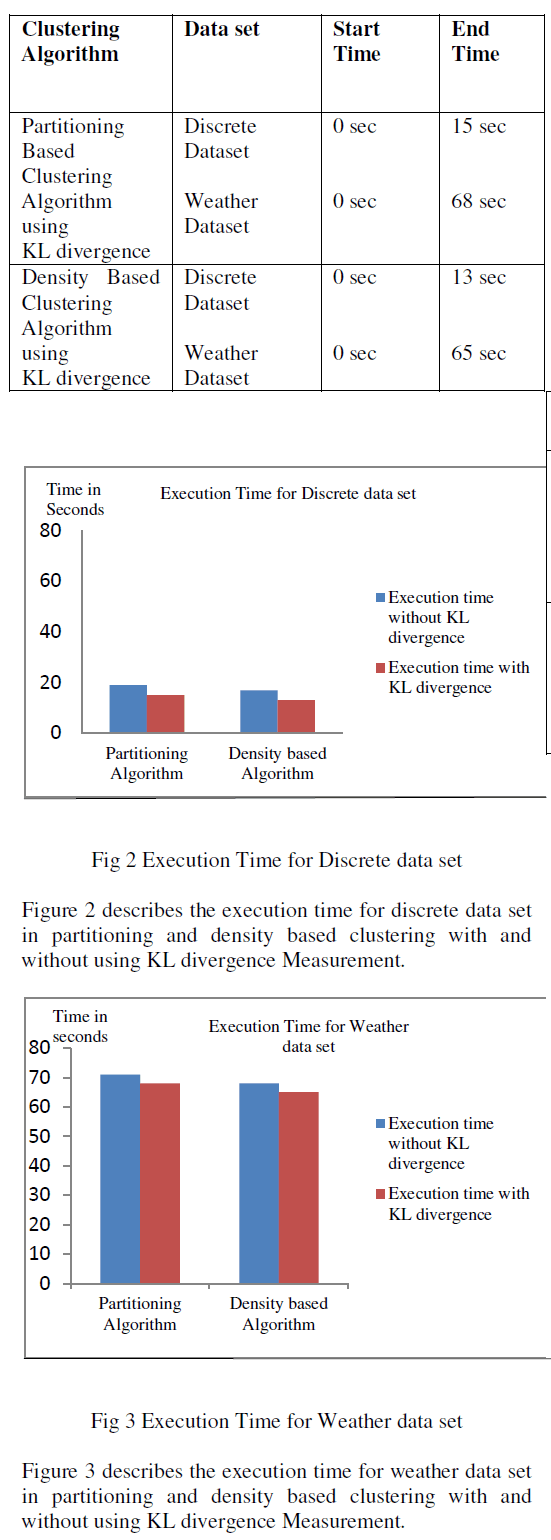
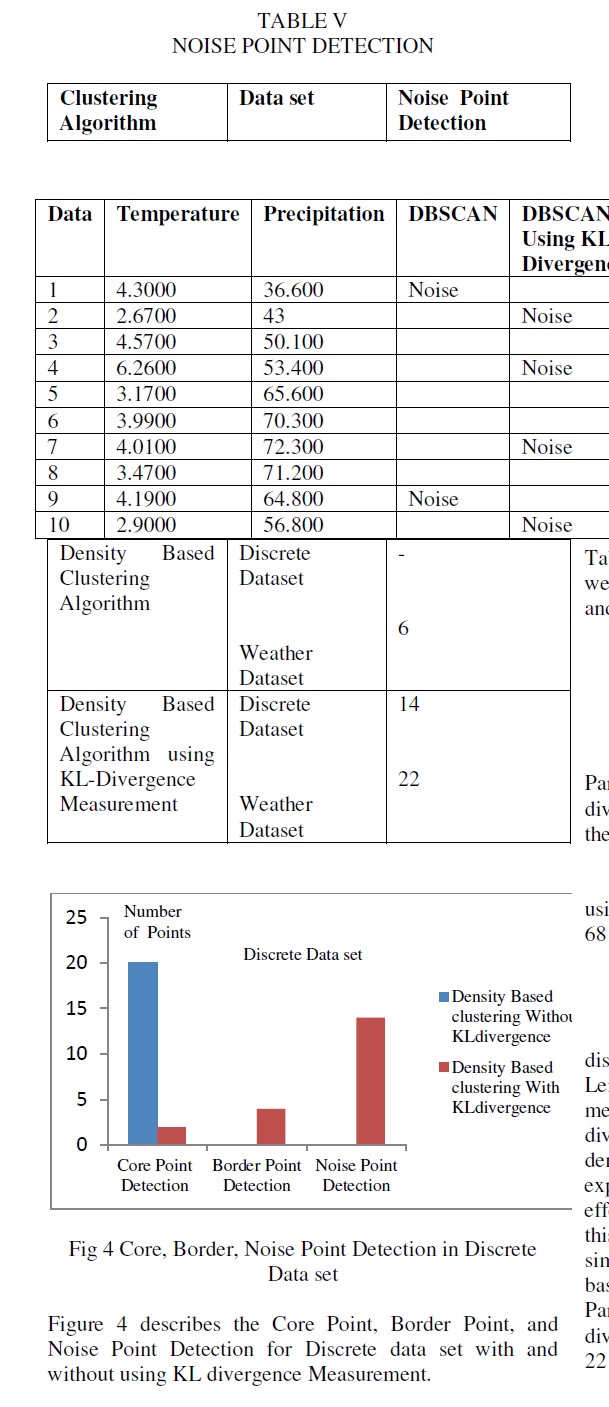
| The execution time of the Partitioning Based clustering using KL divergence reduced to 68 sec and Density Based clustering using KL-Divergence reduced to 65sec, 22 Noise points are detected. The execution time is calculated using Time series function. The Noise Points are calculated using equation 3. |
| Noise Point= [Total number of points] - [{Total number of Core point} + {Total number of Border point}] |
IMPLEMENTATION |
| In this section we first present a Data set used then we present Measurement of KL divergence and we present our evaluation results. |
| A. Data set |
| In our experiment we use discrete data set and weather data set from National Climate Data Center (NCDC) which has 72 records, 18 Attributes and several fields like 1.Statecode 2.Division 3.year 4.Month 5.precipitation 6.Temperature 7.Palmer Drought Severity Index (PDSI) provides the rainfall information 8.CDD and HDD represents the Temperature model 9.SP provides a spring value. |
| B. Experimental setup |
| 1) Hardware |
| Intel core 2 Duo Processor T7500, HDD with 80GB, RAM with 512MB was used 2) Software |
| MATLAB tool was used to implement Distance and Distribution based clustering. In this paper MATLAB with 7.5.0.342(R2007b) which was released at August 15, 2007 is used. |
| C. Measurement of KL divergence: |
 |
| D. Evaluation |
| The result analysis has been performed for distance and distribution based clustering algorithm based on the calculation of execution time and Noise Point Detection. |
| Table I describes the execution time of predefined data set and weather data set in partitioning and density based clustering algorithm without using KL divergence. |
 |
 |
 |
 |
 |
| TABLE VI NOISE POINTS |
| Based on the above result analysis the Partitioning and Density based clustering using KL divergence have reduced the execution time and increased the Noise Point Detection. |
| The Partitioning and Density based clustering using KL divergence have reduced the execution time to 68 sec and 22 Noise Points are detected. |
CONCLUSION & FUTURE WORK |
| In this paper, based on the similarity between the distributions the objects are clustered. The Kullback- Leibler divergence is used for identifying the similarity measurement between objects in discrete cases. KL divergence value is integrated into the partitioning and density based clustering methods. The extensive experiment confirms that KL divergence measurement is effective and efficient. The most important contribution of this paper is to introduce distribution difference as the similarity measure for data and the accuracy is evaluated based on execution time and Noise Point Detection. The Partitioning and Density based clustering using KL divergence have reduced the execution time to 68 sec and 22 Noise Points are detected. |
| In Future Hybrid clustering Algorithms which consist of Partitioning and Density based clustering will be implemented and their performances will be compared with the existing Partitioning and Density based clustering algorithm. |
References |
|