ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
H. B. Kekre1, V. R. Lakshmi Gorty2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this paper, the Kekre’s function is represented in mathematical concept. The Laplace transforms is applied to Kekre’s function and the results are obtained. The graphical representation is shown by MATLAB also to show the Kekre’s function. A generalized representation of Kekre’s function is shown in this paper. To all the assigned order N, of the Kekre’s functions, the solutions are displayed for each example. Linearity property using Laplace transforms when applied to Kekre’s function, is proved in the form of a theorem. For any positive arbitrary value, the transform of Kekre function is obtained and also shown how Kekre’s function is related to inverse Laplace transforms. At the end of examples, the generalized representation of the Laplace transforms of Kekre’s function is formulated.
Keywords |
| Kekre’s function, Laplace transforms, generalized representation, linearity property |
INTRODUCTION |
| Kekre function is defined as |
| for any order, a = 0,1,2,3,...N and a < N. |
| Here N is the order of the Kekre’s function. Transform methods are typically used in many image processing applications such as compression, filtering, enhancement, feature extraction, image texture analysis etc. Using transform domain techniques, it is possible to embed a secret message in different frequency bands of the cover image. There are a number of linear transformations that prove useful in digital image processing. Most commonly used transforms are Discrete Cosine Transform (DCT), Discrete Sine Transform (DST), Walsh, Haar [15] etc. This paper proposes transforms applied to Kekre’s function [15] and can be used for various image processing applications. CBIR technology is implemented in a host of different applications which include art galleries, museums, archaeology [1],[2], architecture/engineering design [3], geographic information systems [5], weather forecast [4], medical imaging [4], trademark databases [6], criminal records [7], World Wide Web like photo sharing and video streaming sites[8]. Some of recent works on speaker identification depend on classical features including cepstrum with many variants [9], sub-band processing technique [10], Gaussian mixture models (GMM) [11], linear prediction coding [12], wavelet transform [13] and neural networks [14]. A lot of work in different applications to engineering fields has been done. But still there is lack of understanding of the mathematical interpretation using Kekre’s function is been observed. The author in the present study, proposes solution to some problems using Kekre’s function which will help further in application problems. In this paper, Kekre’s function is used to solve few problems using Laplace Transforms. |
PRELIMINARY STUDY |
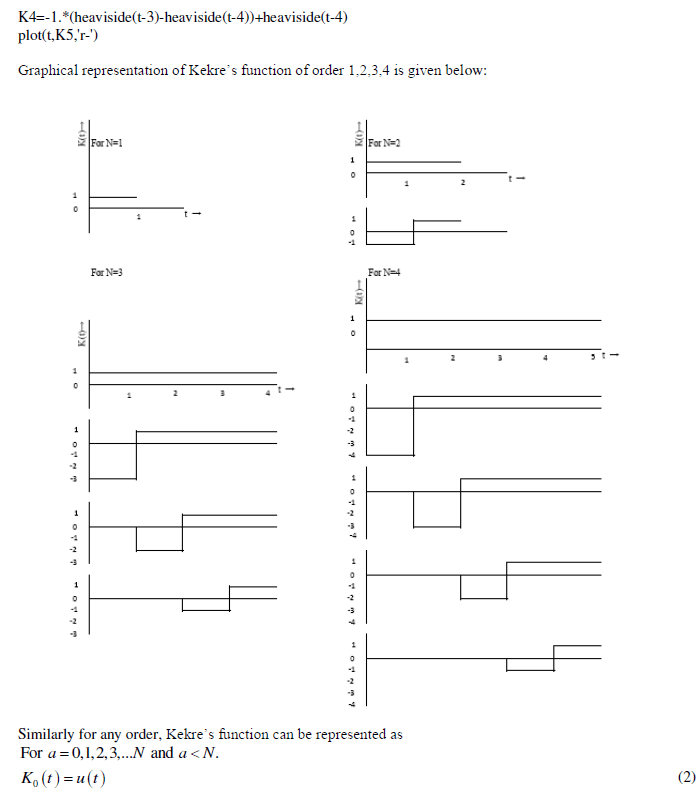
| Here the order of the Kekre’s function is ‘4’. Then the Kekre’s function can be represented as: |
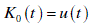 |
 |
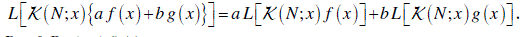 |
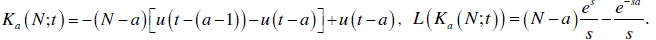 |
 |
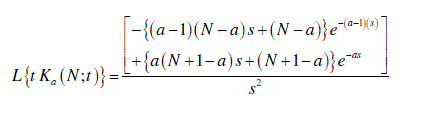 |
 |
 |
 |
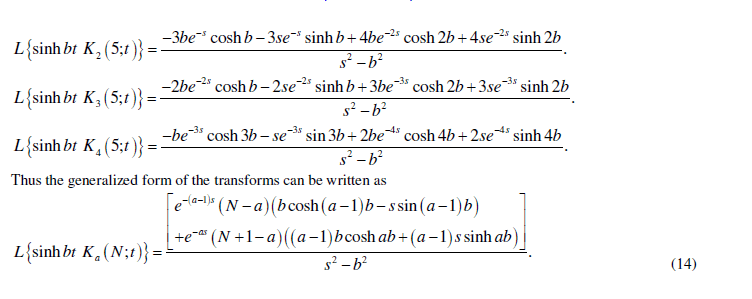 |
RESULTS AND DISCUSSIONS |
| All the examples considering N = 4 or N = 5. These results can be calculated considering for any value of N . The results can be extended to complex variables. The real and imaginary parts of the function will be obtained. The formula can be proved in the similar manner. The elementary functions using Kekre’s function has been evaluated applying Laplace transforms over it. At the end of examples the generalized representation of the Laplace transforms of Kekre’s function is formulated. |
CONCLUSION |
| Kekre’s function has been used in application to image processing and other computer engineering applications. This paper shows mathematical interpretation of Kekre’s function, such that even Mathematicians can use it efficiently. Results are displayed with their calculations and process of the existence of Kekre’s function. |
FUTURE SCOPE |
| This evaluations and observation done by the author in this work can help researchers for the elaborate study in this direction. Evaluation and analysis can be done for higher orders. Continuous transforms of such functions can be studied. Applications to different fields of engineering can fulfill the introduction of such function and its mathematical concept. Table for all the Laplace transforms to Kekre’s function can be calculated. |
References |
|