ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| Brajraj Singh1, D. C. Gupta2, Y M Gupta3 Associate Professor, Faculty of Engineering and Technology, Mody Institute Of Technology and Science (A deemed university, exclusively for woman) Lakshmangarh –332311, India1 Associate Professor, SOS Physics, Jiwaji University, Gwalior-474011, India2 Director, Institute of Technology and Management, Gwalior, India3 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
During the course of present investigation, an effective two-dimensional dynamic interaction potential energy function has been developed to understand the pairing mechanism leading to high-TC superconductivity in copper-oxide superconductors. The present theoretical study has been carried out under perturbation approximation using Dyson diagrammatic formalism and the technique of Fourier transforms. The effective two-dimensional dynamic interaction potential energy function obtained by us is complex in nature from ab-initio. The calculations of coupling strength, Coulomb repulsive parameter and transition temperature for copper-oxide superconductors consisting of one Cu-O layer per unit cell are reported here. Our calculations show that the coupling between Cu-O conducting layers makes the effective potential energy function more attractive as well as less repulsive
Keywords |
| Electron-electron interaction, High-Tc Superconductivity, Strong coupling theory |
INTRODUCTION |
| The discovery of copper oxide superconductors has opened a new era in the field of materials science [1]. Banking on experimental observations that copper-oxide superconductors exhibit layered structure having Cu-O as conducting planes [2-3], a phenomenological layered structure model have been developed to understand pairing mechanism within the framework of BCS theory leading to high-Tc superconductivity. The basic ingredient of layered structure model is that a three-dimensional system is effectively reduced to two-dimensional one. Physically it amounts to the fact that these high-Tc superconductors are constrained systems. From the dynamics point of view it is well known that the system under constrained motion with reduced degree of freedom has complex potential energy function. The imaginary part of the potential energy function accounts for the dissipation of energy function or resistivity in the present case. Number of efforts has been made [4-8] in last two decades after the discovery of cuprate superconductors (CS) but could not succeeded in explaining completely the pairing mechanism abinitio. |
II. MODEL |
| Experimental [9] as well as Theoretical [8] studies of the inverse dielectric response function for YBa2Cu3O7-x, La2-xSrxCuO4 and Bi2CaCu2O8 suggest that CS possess a layered structure and their normal conducting state may be more like a doped semiconductor rather than a metal. Also, the crystallographic studies [10-14] suggest a layered structure for CS. It has been further investigated that the change in the oxygen deficiency in La2x-δBaxCuO4 superconductors develops free charge carriers in copper-oxide conducting planes. We consider an array of two-dimensional layered electron gas model for La-Ba-Cu-O. It is assume that the conduction of charge carriers is very pronounced in copper oxide plane (X-Y plane) and reasonably feeble perpendicular to the plane (Z-direction). Thus the charge carriers are strongly coupled with in the plane but weekly coupled with in the Z direction. The present model is based on assumptions that (i) There is only one Cu-O layer plane per unit cell, (ii) Cu-O plane forms an infinite array of planes along Z-axis, (iii) A non-conducting plane between Cu-O planes is considered as a uniform dielectric medium with a background dielectric constant εb and (iv) The oxygen deficient Cu-O chain stabilizes the charge carriers in the conducting planes. |
| To obtain the effective two-dimensional dynamic interaction potential energy function we start with bare Coulomb potential energy function for the pair of charge carriers existing in consecutive conducting planes given as: |
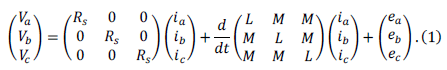 (1) (1) |
| here ε? is dielectric constant in vacuum εb is static dielectric constant of background. |
| The effective potential energy function can be obtained using a Dyson diagrammatic technique. Taking two-dimensional Fourier transform in the X-Y plane, and following the usual procedure [15] we get the bare potential energy function in twodimensional plane as: |
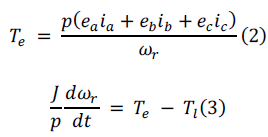 (2) (2) |
here  is momentum transfer wave vector. is momentum transfer wave vector. |
| Now as the charge carriers are confined only in the two-dimensional conducting planes, z and z′ can be represented by discrete variables nd and n′d respectively. Here n and n′ are the numbers required to index the consecutive Oxygen deficient planes and d is the separation between them. From Eq. (2) it is evident that the bare two-dimensional potential energy function depends on (n-n′) and not on n and n′ separately. Hence it is mod of (n-n′) i.e. |n-n′| appears in the expression of bare potential. Consequently Eq. (2) reduces to |
 (3) (3) |
| Assuming that the polarizability for a given conducting plane can be expressed as sum of the polarizabilities of all the possible charge carriers and all conducting planes to be identical, we obtain the effective potential energy function employing Dyson diagrammatic technique and using Discrete Fourier Transform (DFT) [16], as |
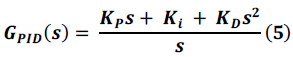 (4) (4) |
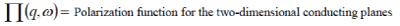 |
and 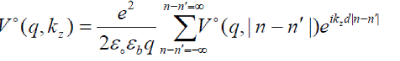 (5) (5) |
| Following the usual technique [15], Eq. (5) yields |
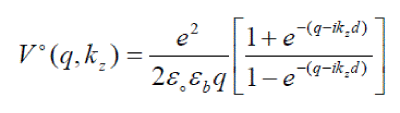 (6) (6) |
| Form Eq.(4) and Eq.(6) we get |
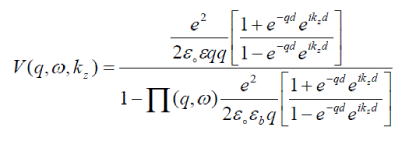 (7) (7) |
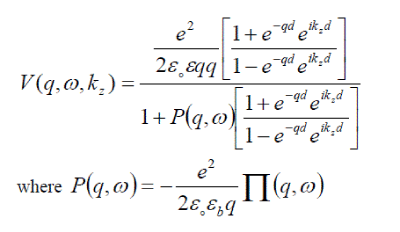 (8) (8) |
where 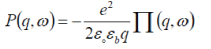 |
A realistic calculation of P(q,ω) requires a many-body treatment (marginal Fermi-liquid treatment) of a strongly correlated 2D system. However, here we use an RPA expression for P(q,ω), in order to see the coupling effects in a simple manner. We take P(q,ω) [17] as 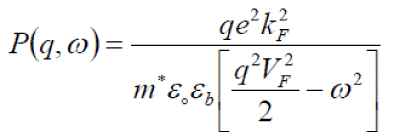 (9) (9) |
| where F k and F V are Fermi wave vector and Fermi velocity, respectively and m* is effective mass. |
III. RESULT AND DISCUSSION |
| 3.1 Analysis of Effective potential |
| Effective two-dimensional dynamic potential energy function obtained in Eq. (8) is complex from ab-initio. Therefore, the complex nature of present potential energy function, responsible for the resistivity of the material has been included in a natural way. This gets rid of all ad-hoc prescriptions as are being used in earlier investigations [5-8] to make the effective potential energy function complex in nature. |
| 3.2 Cut-off Frequency and Attractive and Repulsive Frequency Ranges |
| The cut-off frequency, which gives the upper cut-off limit for attractive potential energy function, is obtained as follows: The average dynamic permittivity ε(q,ω) is computed as |
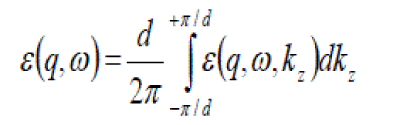 |
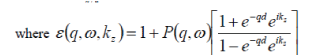 |
| Thus on integrating, Eq. (10) yields |
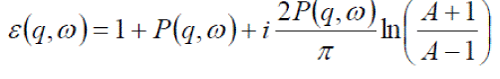 |
| where A=eqd |
| The zeros of Real ε(q,ω) i.e. Re ε(q,ω) give the cut-off frequency ωc. Hence we have |
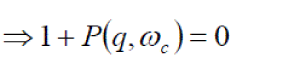 (12) (12) |
| On solving Eq. (12) and using Eq. (9) we get |
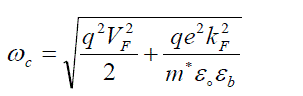 (13) (13) |
| The frequency range in which interaction potential energy function is attractive can be obtained as follows. Using Eq. (13) and Eq. (9) (RPA polarization) Re ε(q,ω) becomes |
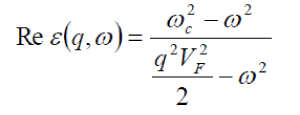 (14) (14) |
| and the range in which interaction potential energy function is attractive, is defined as Reε(q,ω)< 0 Thus there are two possibilities to fulfill this condition: |
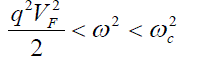 (15) (15) |
and 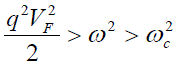 (16) (16) |
| Second possibility is automatically ruled out from Eq. (13). Thus first condition i.e. Eq. (15) gives the frequency range in which the effective two-dimensional dynamic interaction potential energy function is attractive, viz. |
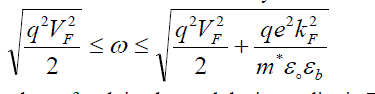 (17) (17) |
| For the values of ω, lying beyond the inequality in Eq. (17), V(q, ω) is repulsive. |
| 3.3 Comparison of Effective and Bare Potential Energy Functions |
| We have investigated the behavior of bare and effective potential energy functions as given by Eq. (6) and Eq. (8) respectively with respect to qd for a given Cosθ (where θ = Kzd ) and ω. For the sake of completeness a comparison of present results has been done with that of obtained by earlier investigators [5-8] for Cosθ=0.9 and ω=1013 Hz. The value of ω is chosen with in the range for which the dielectric response function leads to the formation of cooper pairs. The real of effective potential energy function of the present model exactly the same as earlier workers [5-8]. The total effective potential energy function of the present model is linear sum of its real and imaginary parts and therefore, it is much more attractive. Hence, it is envisaged that if a sample is so prepared that charge carriers in conducting planes are guided such that they practically suffer elastic collisions in the forward direction (q is small and Cosθ ≈ 1), the sample has enhanced probability of exhibiting high transition temperature. |
| 3.4. Calculation of Coupling strength (λ), Coulomb repulsive parameter (μ*) and Transition temperature (Tc) |
| Employing the present formalism, we have calculated λ, μ* and Tc for La2-xSrxCuO4 cuprate superconductor at x=0.15, which consists of one Cu-O layer per unit cell. For computation we used m*=4me, kF=0.2833Å-1, d=13.25Å, qc=0.0239Å-1 and εο=22 [18]. We obtained λ= 1.54 and μ*=0.02 and Tc=39.6 K. We thus find that our calculated value of Tc is in good agreement with the experimentally observed value [19-20]. The calculations based on present formalism for 123 superconductors are under progress. |
IV. CONCLUSION |
| In the present investigation model developed for layered structure systems have been made mathematically consistent and physically logical ab-initio. As a matter of fact the reduction of three-dimensional system to an effective two-dimensional system gives reduced degree of freedom. The occurrence of complex nature of an effective potential energy function is a direct consequence of the reduction of degree of freedom. Earlier investigations have used an ad-hoc prescription in an artificial way in order to incorporate reduced degree of freedom. Therefore, it can be concluded that our formalism provides mathematically correct and physically logical layered structure model. |
References |
|