Locational Marginal Pricing In Restructured
Power Market

K.Kamal dass; P.Kanakaraj; M.Prabavathi

Locational Marginal Pricing In Restructured Power Market

K.Kamal dass¹, P.Kanakaraj², M.Prabavathi³

P.G Scholar (P.S.E),M.Kumarasamy College of Engineering,, India.
Asst. Professor, Dept. of EEE, M.Kumaransamy College of Engineering, India.
Research scholar,Pandichery Engineering college,Pondichery, India.

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

The impact of congestion in the transmission corridor is one of the major issues in the competitive electricity market. The paper presents power word simulator tools for determining the congestion quantities and locational marginal price due to line over load in competitive electricity environment.

INDEX TERMS

Locational Marginal Priceing(LMP), Congestion Management(CM), Power Market, Optimal Power Flow(OPF)

INTRODUCTION

In the restructured environment, the process of the power system such as generation, transmission, distribution and system control are distinct entities and market participants interrelate themselves in order to buy or sell the electric power so as to maximize their turnover. To meet the preferred trading, power flow in the transmission network invades some of the physical restrictions of the transmission systems. Due to this, transmission system gets congested. Congestion may occur due to lack of management between generation and transmission utilities or as a result of unexpected eventualities such as power producers outage, unexpected increase of load demand, or failure of equipment. The unattractive effect of the congestion causes instability of the system security and increase of the power cost. Congestion can be alleviated by rescheduling of real power of generators, load limitation and operation of phase-shifters or FACTS devices. An appropriate control action is needed effectively to mitigate the line overloads to the safety limits.

There are numerous publications available that describes methods for relieving congestion in restructed power system. Ashwani Kumar et al [1] have obtainable a bibliographical review on congestion management systems in a competitive electricity market. One of the most skillful and an understandable technique of congestion management is rescheduling the power outputs of generators in the system. In [2], two effectual methods are suggested for solving congestion management problem in a day ahead electricity market by generator rescheduling. Differential Evolution (DE) algorithm has been established to solve the problem of power congestion by rescheduling of real power of generators, which are selected by based on sensitivity to overloaded network in [3],[4]. A zonal/cluster-based congestion management method has been offered in [5] for optimal rescheduling of reactive power for the generators and capacitors in the most subtle zones. A new iterative LMP calculation method is suggested to avoid the main hitches with the DC power flow based LMP calculations In [6]. LMP is usually crumbled into three components marginal cost of energy, loss and congestion which is explored in [7]. Particle Swarm Optimization is employed to solve the OPF problem construction for congestion management using re-dispatch of transactions in a pool-co model [8]. Both the real and reactive power flow influence factors for generators as well as loads have been presented to recognize the most suitable generators and loads to contribute in congestion management [9].The concept of game theory in the deregulated electricity market has established illustratively to show that how symmetry point of electricity market departs under the strategic gaming in [10]. Eugene Litvinov et al [11] have discussed the pricing of marginal transmission network losses in the locational marginal pricing approach in the ISO New England standard market design. Four different calculation models and consistent properties on LMP depending on different market designs are discussed in [12]. A multilayer feed forward neural network is proposed for eliminating line overloads in real time for deregulated electricity market [13]. In [14], congestion release can be attained by re dispatch method considering the collective operation of hydro and thermal generating companies in an electricity market. Flexible AC Transmission System supervisors plays a important role in increasing loadability and improving congestion in the network. In [15], a Mixed Integer Nonlinear Programming approach for congestion management using optimal placement of Thyristor Controlled Series Compensators has been discussed.

LMP includes the cost of supplying the more expensive electricity in congestion places, thus providing a accurate, market based method for pricing energy that includes the cost of congestion. This work focuses on manipulative, Locational Marginal Pricing value at the time of congestion and locate the spots of congestion in the IEEE 6 bus system under various critical conditions due the different transmission line outage, the results are found efficient in reducing the congestion with economic operation.

MATHEMATICAL FORMULATION

A. Proposed LMP Model

In real power market security checks are performed after the market clearing and LMP calculations. In the security check Step, reactive power may also be considered .The influence of reactive power can be taking into account if the full AC instead of DC power flow constraints is considered in the procedure of LMP calculations. Non linear programming model is not employed because of the problem in solution robustness algorithm and the difficulties in the software development for practical implementation.

The following model is proposed for the iterative LMP calculations

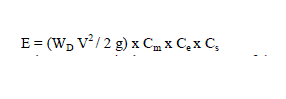Where LFAC, DAC and offsetAC are not preset before resolving this model. Instead they are attained from the solution of the full AC power flow.

B. Loss and Loss Sensitivity Vector

At first, offsetAC , LFAC and DAC can be set equal to zero. Solving the proposed model gives a generator dispatch PG.Then the full AC power flow can be solved. Choosing power injection into the system as the positive direction of power, the active power flow of a branch can be calculated by

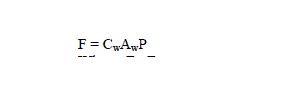The total system loss is an accumulation of the losses of all branches

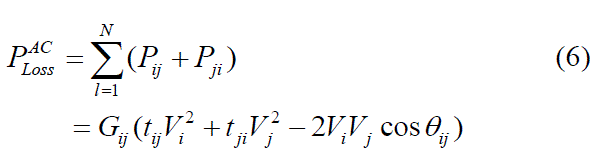Where node i and j are the ends of portion l.

Now, it is not difficult to build the following equation, signifying the sensitivity of the system total loss to the nodal power injections:

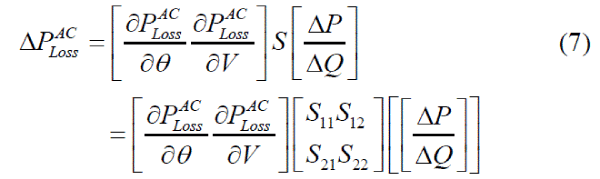Sensitivity matrix S is the inverse of the jacobian matrix of the AC power flow equations. For the suggested model, the sensitivities of active power injections to the system loss are preferred, which is specified by the following equation:

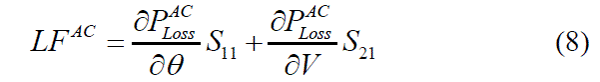Then the loss offset can be easily obtained by

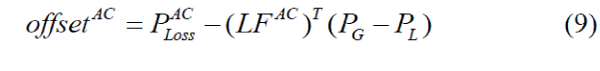C. Nodal Fictitious Demands and Loss Distribution Factors

By analogy with the approximation idea of the DC power flow model, the following approximate formula can be derived:

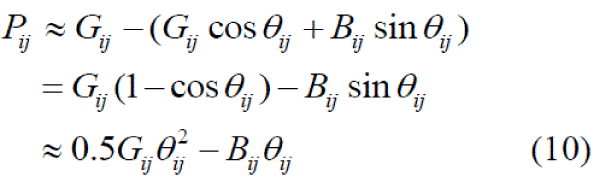For the proposed method, the full AC power flow is solved. Accurate branch flows and branch losses can be obtained. According to the above discussion, the loss of each branch can be divided into two equal halves and attached to the two nodes of the branch. The fictitious nodal demand is then defined as follows:

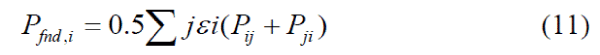Where jεi means node i and j are the two ends of a branch. Now, each element of DAC can be determined as the ratio of the corresponding fictitious nodal demands to AC Loss P and calculated as

D. Calculation Procedure and Convergence

The basic process of the suggested LMP calculation method is shown in the Fig. 1. The situation for testing convergence is given as follows. Associate the clearing results for each generator with the results of the preceding iteration. If the difference in the output of each generator is smaller than a predefined tolerance, then stop the iteration. Otherwise, continue the iteration. If PG converges after the (i+1)th iteration, the solutions of AC power flow obtained at the ith and the (i+1)th iteration are almost the same. Thus LFAC, DAC and offsetAC all converge.

Although LFAC, offsetAC and DAC are not preset in the proposed model, it can be proved that the primary solution and the result of each LMP and its congestion component are autonomous of the selection of reference bus.

Figure 1. Flow chart for calculation of LMP

AN EXAMPLE

This calculation procedure has been applied to several test system. If not particularly pointed out, the initial values of LFAC,PLOSS and DAC are all zeros.

A. IEEE 6-Bus System

The diagram of the slightly modified IEEE Sixbus system is shown in Fig.2..Table I lists the line impedance and power flow limits.

The voltage magnitude of reference bus and PV buses are all set equal to 1.0.p.u. The convergence criterion is the maximum power output error of all units between two successive iterations is lower than 0.01 MW. Energy Loss LMP + LMP + LMPCongestion ,LMP at each bus are the same for all cases. The initial outputs for all generators(PG) are set to 0.

B. Dicussions on Convergence of the Proposed Method

For the zero initial values of LFAC,OFFSETAC and DAC the generator dispatch results are the same at the first iteration for any choice of slack bus. At the second iteration, the clearing results for(PG) are slightly different for different slack bus. At convergences, the clearing results for(PG)are almost the same because PLOSS is almost equal to the power loss AC LOSS P obtained by the AC power flow.

Figure 2. IEEE Six bus system

Table 1 LINE DATA

The bus 1,2 and 3 are the Generator buses. Where bus 1 is a reference bus the capacity of the generator 2 and 3 are 50 MW and 60 MW respectively. The magnitude of the generator bus are 1.05,1.05 and 1.07 respectively. Bus 4,5 and 6 are Load buses the load values 70 MW for each load buses. The table I shows the Line datas.

RESULT AND DISCUSSION

In this work the LMP value calculated by using the software of Power World Simulator. The power world simulator experiment the results are following

1. Without Congestion

Figure .3. OPF Diagram for IEEE 6 bus system

The above Figure.3. shows a optimal power flow diagram of a IEEE 6 bus system with using of power world simulator. The locational marginal price of the real power flow is determined. This power flow is very economic with given line constraints. Table II shows the MW Marginal Cost at optimal power flow.

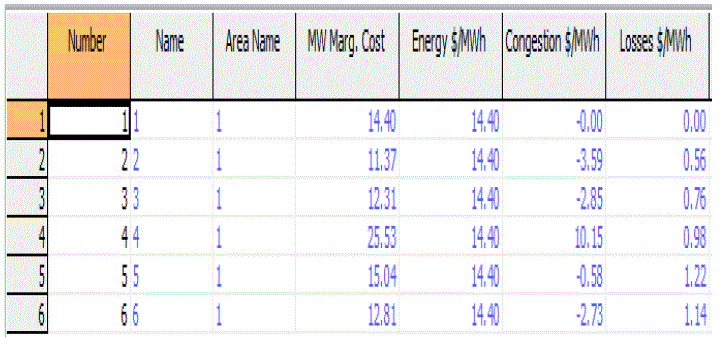Table 2: MW MARGINAL COST

2. Congestion cases

Congestion is a phenomenon that affects the entire system and, as such, all the players in electricity markets. Once a line becomes congested, the entire system suffers the resulting impacts. Congestion has come to play an important role in power systems in the restructuring of the electricity industry.

The optimal operation of the system requires the optimization of a specified objective function subject to ensuring that no violation of the constraints occurs. The utilities were vertically integrated, owning and controlling both generation and transmission, so any conflict between security and economics was resolved by the single decision-making entity, which both owned and controlled all the facilities. In this work power world simulator is used to manage the congestion and calculate the congestion cost for the LMP.

The analysis made by different line outages. When the line 1-4 is outage the line 2-4 will be get over loaded it is shown in the following figure.4.

Figure 4. OPF Diagram for Line 1-4 Outage.

In congestion line the range of current flow is 169% of the original MVA rate of the line 2 to line 4. According to this congestion the LMP value are calculated for each bus it shows in the table III.

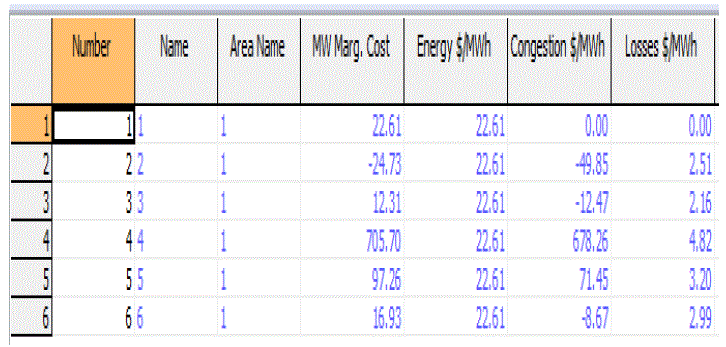Table 3: MW Marginal Cost at Line 1-4 Outage Condition

According to the different line outages the final total cost and average bus marginal cost are calculated for IEEE 6 bus system. This cost comparison is shows in the above table IV.

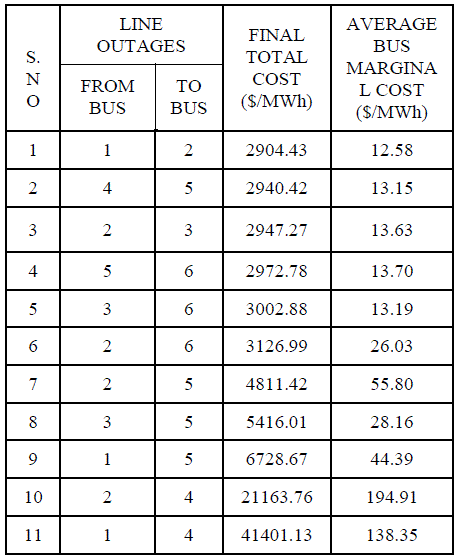TABLE 4: Comparative Study of Different Line Outages

CONCLUSION

In this project, a new software tool named power world simulator is used to determine the locational marginal pricing for congestion management in electricity market in IEEE 6 bus system. Analysis has been made on locational marginal pricing value at each buses under various line outages cases. It is observed finally that the congestion occurs during line outages. Thus, the sensitivity of each line is observed and thereby stability and economic operation of the power system is maintained. Also it is found that marginal cost satisfies both power producers and consumers.

References

Ashwani Kumar, S.C. Srivastava, and S.N. Singh, Congestion management in competitive Power Systems Research power market: a bibliographical survey, Electric, Vol. 76, pp.153–164, 2005.
K.Vijayakumar, “Multiobjective Optimization Methods for Congestion Management in Deregulated Power Systems”, Journal of Electrical and Computer Engineering, Vol. 2012 (2012).
Kundu, Saikat, “Congestion Management by Rescheduling of Active Power of Generators using Generator Sensitivity Based on Differential Evolution”, power Engineering- Master’s degree theses, Jadavpur University (2013).
R.Rajathy,R.Gnanadass ,K.Manivannan and Harish kumar, “Differential Evolution-Based Algorithm for Congestion Management in a Deregulated Environment”, The IUP Journal of Electrical & Electronics Engineering, Vol. 4, No. 1, pp. 46-64, January 2011.
Ashwani Kumar , S C Srivastava and S N Singh,” A Zonal Congestion management.approach using real and reactive power rescheduling ” , IEEE transaction on power systems, Vol 19, No.1, pp. 554—562, February 2004.
Basanta Kumar Panigrahi, “Locational Marginal Pricing (LMP) in Deregulated Electricity Market”, International Journal of Electronics Signals and Systems, Vol-1, No.2, 2012.
M. Rivier and J. I. Perez-Arriaga, “Computation and decomposition of spot prices for transmission pricing,” Proceedings of. 11th PSC Conference, Avignon, France (1993).
Tulika Bhattacharjee and Ajoy Kumar Chakraborty, “Congestion management in a deregulated power system by rescheduling of sensitive generators and load curtailment using PSO”, International Journal of Emerging Technology and Advanced Engineering, Vol. 2, No. 3, (2012).
Kumar, V. Kumar, and S. Chanana, “Generators and Loads Contribution Factors Based Congestion Management in Electricity Markets”, International Journal of Recent Trends in Engineering, Vol. 2, No. 6, November (2009) .
N S Modi, and B R Parekh, “Transmission Network Congestion in Deregulated Wholesale Electricity Market”, Proceedings of the International Multi Conference of Engineers and Computer Scientists, Hong Kong ,Vol. 2, (2009).
Eugene Litvinov, Member, IEEE, Tongxin Zheng, Member, IEEE, Gary Rosenwald, and Payman Shamsollahi, Senior Member, IEEE, “Marginal Loss Modeling in LMP Calculation”, IEEE Transactions on power systems, Vol. 19, No. 2, May (2004).
Yong Fu, and Zuyi Li, “Different Models and Properties on LMP Calculations”, IEEE Power Engineering Society general meeting, (2006).
Sujatha Balaraman and N. Kamaraj, “Real Time Congestion Management in Deregulated Electricity Market Using Artificial Neural Network “,Iranian Journal of Electrical and Computer Engineering, Vol. 10, No. 1, (2011).
Kanwardeep Singh, N.P. Padhy, and J. Sharma, “Congestion management considering hydro–thermal combined operation in a pool based electricity market”, Electrical Power and Energy Systems, vol.33, pp.1513–1519, (2011).
Kanwardeep Singh, Vinod K. Yadav, Arvind Dhingra, “Congestion Management Using Optimal Placement of TCSC in Deregulated Power System”, International Journal on Electrical Engineering and Informatics – Vol.4, No. 4, December (2012).