ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
R.Pavitha1 and Ms T.Joyce Selva Hephzibah M.Tech.2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The project proposes an automatic support system for stage classification using probabilistic neural network based on the detection of cancer region through thresholding method for medical application. The detection of the breast cancer is a challenging problem, due to the structure of the cancer cells. This project presents a segmentation method, wavelet based threshold method, for segmenting mammographic images to detect the Breast cancer in its early stages. The threshold will be determined by biclustering an image based on row and column separation. The artificial neural network will be used to classify the stage of image that is abnormal or normal. The manual analysis of this samples are time consuming, inaccurate and requires intensive trained person to avoid diagnostic errors. The segmentation results will be used as a base for a Computer Aided Diagnosis system for early detection of cancer from mammographic images which will improves the chances of survival for the patient. Discrete wavelet transform technique is used for extracting texture features and it decomposed the image into four levels for getting the edge details in horizontal and vertical direction. The Cooccurrence matrix will be determined for these two high frequency sub bands for finding the texture features. Probabilistic Neural Network with radial basis function will be employed to implement an automated breast cancer classification. Decision making was performed in two stages: feature extraction using Wavelet transformation followed by GLCM and the classification using PNN-RBF. The performance of the PNN classifier was evaluated in terms of training performance and classification accuraci. Probabilistic Neural Network gives fast and accurate classification than other neural networks and it is a promising tool for classification of the cancers.
INTRODUCTION |
OVERVIEW |
| Cancer refers to the uncontrolled multiplication of a group of cells in a particular location of the body. A group of rapidly dividing cells may form a lump, micro calcifications or architectural distortions which are usually referred to as tumors. Breast cancer is any form of malignant tumor which develops from breast cells. Breast cancers are traditionally known to be one of the major causes of death among women. Mortality rates due to breast cancer have been reducing due to better diagnostic facilities and effective treatments. One of the leading methods for diagnosing breast cancer is screening mammography. This method involves X-ray imaging of the breast. Screening mammography examinations are performed on asymptomatic women to detect early, clinically unsuspected breast cancer. Early detection of breast cancer through screening and diagnostic mammography increases breast cancer treatment options and survival rates. Unfortunately, due to the human factor involved in the screening process, detection of suspicious abnormalities is prone to a high degree of error. |
| As a result of this error rate, biopsies are frequently performed on benign lesions, resulting in unwarranted expenditure and anxiety for the patient involved. The cost associated with errors due to misclassification of mammograms is considerable. This is because of the fact that false negatives are a huge problem in screening mammography as early detection can reduce treatment cost, time and effectiveness to a great extent. False negatives affect all three parameters as early detection is not an option with an incorrect diagnosis. A major reason for these errors is due to the fact that radiologists depend on visual inspection. During manual screening of a large number of mammograms, radiologists may get easily worn out, missing out vital clues while studying the scans. |
| To offset these effects, tremendous effort is being made to automate the process of mammographic screening. Automated screening of mammograms or computer-aided diagnosis (CAD) of breast cancer is a vast field of research. Classifier systems have been widely used in medical diagnosis. Though the most important factor in diagnosis is evaluation of data taken from patients by human experts, expert systems and various artificial intelligence techniques for classification aid radiologists to a great extent Any computer-aided diagnosis system is based on artificial intelligence (AI) techniques. The pipeline used in a CAD system for breast cancer detection is similar to any other AI-based system and consists of preprocessing, breast region segmentation, feature extraction and classification. A major difference between computer-aided detection of breast cancer and other AI-based technologies is that breast cancer detection using CAD systems requires human intervention for interpreting the final results. |
| Automated detection and classification of cancers in different medical images is motivated by the necessity of high accuracy when dealing with a human life. Also, the computer assistance is demanded in medical institutions due to the fact that it could improve the results of humans in such a domain where the false negative cases must be at a very low rate. It has been proven that double reading of medical images could lead to better cancer detection. But the cost implied in double reading is very high, that’s why good software to assist humans in medical institutions is of great interest nowadays. Conventional methods of monitoring and diagnosing the diseases rely on detecting the presence of particular features by a human observer. Due to large number of patients in intensive care units and the need for continuous observation of such conditions, several techniques for automated diagnostic systems have been developed in recent years to attempt to solve this problem. Such techniques work by transforming the mostly qualitative diagnostic criteria into a more objective quantitative feature detection problem. |
| The automated detection of breast magnetic resonance images by using some prior knowledge like pixel intensity and some anatomical features is proposed. Currently there are no methods widely accepted therefore automatic and reliable methods for cancer detection are of great need and interest. The application of PNN in the classification of data for mammogram images is prototyped here for solving the problem of inaccurate detection and classification of breast cancer from the mammographic images. |
| Basic Image Classifications |
| There are 3 types of images used in Digital Image Processing. They are |
| 1. Binary Image |
| 2. Gray Scale Image |
| 3. Colour Image |
Binary Image |
| A binary image is a digital image that has only two possible values for each pixel. Typically the two colors used for a binary image are black and white though any two colors can be used. The color used for the object(s) in the image is the foreground color while the rest of the image is the background color. |
| Binary images are also called bi-level or two-level. This means that each pixel is stored as a single bit (0 or 1).This name black and white, monochrome or monochromatic are often used for this concept, but may also designate any images that have only one sample per pixel, such as grayscale images Binary images often arise in digital image processing as masks or as the result of certain operations such as segmentation, thresholding, and dithering. Some input/output devices, such as laser printers, fax machines, and bi-level computer displays, can only handle bi-level images |
Gray Scale Image |
| A grayscale Image is digital image is an image in which the value of each pixel is a single sample, that is, it carries only intensity information. Images of this sort, also known as black-and-white, are composed exclusively of shades of gray (0-255), varying from black(0) at the weakest intensity to white(255) at the strongest. |
| Grayscale images are distinct from one-bit black-andwhite images, which in the context of computer imaging are images with only the two colors, black, and white (also called bi-level or binary images). Grayscale images have many shades of gray in between. Grayscale images are also called monochromatic, denoting the absence of any chromatic variation. |
Colour image |
| A (digital) color image is a digital image that includes color information for each pixel. Each pixel has a particular value which determines it’s appearing color. This value is qualified by three numbers giving the decomposition of the color in the three primary colors Red, Green and Blue. Any color visible to human eye can be represented this way. The decomposition of a color in the three primary colors is quantified by a number between 0 and 255. For example, white will be coded as R = 255, G = 255, B = 255; black will be known as (R,G,B) = (0,0,0); and say, bright pink will be : (255,0,255). |
Literature survey |
| a) Computer-aided diagnostic system based on wavelet analysis for microcalcification detection in digital mammograms |
| Clusters of microcalcifications in mammograms are an important early sign of breast cancer in women. In this paper an approach is proposed to develop a Computer-Aided Diagnosis (CAD) system that can be very helpful for radiologist in diagnosing microcalcifications’ patterns in digitized mammograms earlier and faster than typical screening programs. The proposed method has been implemented in three stages: (a) the region of interest (ROI) selection of 32×32 pixels size which identifies clusters of microcalcifications, (b) the feature extraction stage is based on the wavelet decomposition of locally processed image (region of interest) to compute the important features of each cluster and (c) the classification stage, which classify between normal and microcalcifications’ patterns and then classify between benign and malignant microcalcifications. In classification stage, four methods were used, the voting K-Nearest Neighbor classifier (KNN), Support Vector Machine (SVM) classifier, Neural Network (NN) classifier, and Fuzzy classifier. The proposed method was evaluated using the Mammographic Image Analysis Society (MIAS) mammographic databases. The proposed system was shown to have the large potential for microcalcifications detection in digital mammograms. |
| Methodologies: wavelet, support vector machine, neural network, and fuzzy classifier. |
| b) Integrated wavelets for enhancement of microcalcifications in digital mammography. |
| This paper presents a new algorithm for enhancement of microcalcifications in mammograms. The main novelty is the application of techniques we have developed for construction of filter banks derived from the continuous wavelet transform. These discrete wavelet decompositions, called integrated wavelets, are optimally designed for enhancement of multiscale structures in images. Furthermore, we use a model based approach to refine existing methods for general enhancement of mammograms resulting in a more specific enhancement of microcalcifications. We present results of our method and compare them with known algorithms. Finally, we want to indicate how these techniques can also be applied to the detection of microcalcifications. |
| Methodologies: Digital mammography, enhancement, integrated wavelets, microcalcification. |
| c) Computerized Detection of Malignant Tumors on Digital Mammograms |
| This paper presents a tumor detection system for fully digital mammography. The processing scheme adopted in the proposed system focuses on the solution of two problems. One is how to detect tumors as suspicious regions with a very weak contrast to their background and another is how to extract features which characterize malignant tumors. For the first problem, a unique adaptive filter called the iris filter is proposed. It is very effective in enhancing approximately rounded opacities no matter what their contrasts might be. Clues for differentiation between malignant tumors and other tumors are believed to be mostly in their border areas. This paper proposes typical parameters which reflect boundary characteristics. To confirm the system performance for unknown samples, large scale experiments using 1212 CR images were performed. |
| Methodologies: Boundary detection, computer-aided diagnosis, mammography, tumor detection. |
| d) Optimizing wavelet transform based on supervised learning for detection of microcalcifications in digital mammograms |
| A novel technique for optimizing the wavelet transform to enhance and detect microcalcifications in mammograms was developed based on the supervised learning Method. In the learning process, a cost function is formulated to represent the difference between a desired output and the reconstructed image obtained from weighted wavelet coefficients for a given mammogram. This cost function is then minimized by modifying the weights for wavelet coefficients via a conjugate gradient algorithm. The Least Asymmetric Daubechies’ wavelets were optimized with 44 regionsof- interest as the training set using a jaclrlriiife method. The performance of the optimized wavelets achieved a sensitivity of 90% with specificity of SO%, which outperforms our current scheme based on a conventional wavelet transform. |
| e) Mammographic Feature Enhancement by Multiscale Analysis |
| This paper introduces a novel approach for accomplishing mammographic feature analysis by over complete multiresolution representations. We show that efficient representations may be identified within a continuum of scale-space and used to enhance features of importance to mammography. Methods of contrast enhancement are described based on three over complete multiscale representations: 1) the dyadic wavelet transforms (separable), 2) the p transform (non separable, non orthogonal), and 3) the hexagonal wavelet transform (non separable). Multiscale edges identified within distinct levels of transform space provide local support for image enhancement. Mammograms are reconstructed from wavelet coefficients modified at one or more levels by local and global nonlinear operators. In each case, edges and gain parameters are identified adaptively by a measure of energy within each level of scale-space. We show quantitatively that transform coefficients, modified by adaptive nonlinear operators, can make more obvious unseen or barely seen features of mammography without requiring additional radiation. Our results are compared with traditional image enhancement techniques by measuring the local contrast of known mammographic features. We demonstrate that features extracted from multiresolution representations can provide an adaptive mechanism for accomplishing local contrast enhancement. By improving the visualization of breast pathology, we can improve chances of early detection while requiring less time to evaluate mammograms for most patients. |
EXISTING SYSTEM |
Threshold based Segmentation |
| The simplest method of image segmentation is called the thresholding method. This method is based on a clip-level (or a threshold value) to turn a gray-scale image into a binary image. The key of this method is to select the threshold value (or values when multiple-levels are selected). Several popular methods are used in industry including the maximum entropy method, Otsu's method (maximum variance), and k-means clustering. Recently, methods have been developed for thresholding computed tomography (CT) images. The key idea is that, unlike Otsu's method, the thresholds are derived from the radiographs instead of the (reconstructed) image. |
Design Steps |
| (1) Set the initial threshold T= (the maximum value of the image brightness + the minimum value of the image brightness)/2. |
| (2) Using T segment the image to get two sets of pixels B (all the pixel values are less than T) and N (all the pixel values are greater than T); |
| (3) Calculate the average value of B and N separately, mean up and un. |
| (4) Calculate the new threshold: T= (ub+un)/2 |
| (5) Repeat Second steps to fourth steps upto iterative conditions are met and get necessary region from the brain image. |
| Clustering methods |
| The K-means algorithm is an iterative technique that is used to partition an image into K clusters. The basic algorithm is: |
| 1. Pick K cluster centers, either randomly or based on some heuristic |
| 2. Assign each pixel in the image to the cluster that minimizes the distance between the pixel and the cluster center. |
| 3. Re-compute the cluster centers by averaging all of the pixels in the cluster |
| 4. Repeat steps 2 and 3 until convergence is attained (e.g. no pixels change clusters) |
| In this case, distance is the squared or absolute difference between a pixel and a cluster center. The difference is typically based on pixel color, intensity, texture, and location, or a weighted combination of these factors. K can be selected manually, randomly, or by a heuristic. |
| This algorithm is guaranteed to converge, but it may not return the optimal solution. The quality of the solution depends on the initial set of clusters and the value of K. |
| In statistics and machine learning, the k-means algorithm is a clustering algorithm to partition n objects into k clusters, where k < n. It is similar to the expectation-maximization algorithm for mixtures of Gaussians in that they both attempt to find the centers of natural clusters in the data. The model requires that the object attributes correspond to elements of a vector space. The objective it tries to achieve is to minimize total intra-cluster variance, or, the squared error function. The k-means clustering was invented in 1956. The most common form of the algorithm uses an iterative refinement heuristic known as Lloyd's algorithm. Lloyd's algorithm starts by partitioning the input points into k initial sets, either at random or using some heuristic data. It then calculates the mean point, or centroid, of each set. It constructs a new partition by associating each point with the closest centroid. Then the centroids are recalculated for the new clusters, and algorithm repeated by alternate application of these two steps until convergence, which is obtained when the points no longer switch clusters (or alternatively centroids are no longer changed). Lloyd's algorithm and k-means are often used synonymously, but in reality Lloyd's algorithm is a heuristic for solving the k-means problem, as with certain combinations of starting points and centroids, Lloyd's algorithm can in fact converge to the wrong answer. Other variations exist, but Lloyd's algorithm has remained popular, because it converges extremely quickly in practice. In terms of performance the algorithm is not guaranteed to return a global optimum. The quality of the final solution depends largely on the initial set of clusters, and may, in practice, be much poorer than the global optimum. Since the algorithm is extremely fast, a common method is to run the algorithm several times and return the best clustering found. A drawback of the k-means algorithm is that the number of clusters k is an input parameter. An inappropriate choice of k may yield poor results. The algorithm also assumes that the variance is an appropriate measure of cluster scatter. |
Design Steps: |
| K-Means algorithm is an unsupervised clustering algorithm that classifies the input data points into multiple classes based on their inherent distance from each other. |
| Step l: Increment value= ([max – min]/number of clusters) |
| Step 2: Initialize the centroids with k random intensities. |
| Step 3: Find the difference between the four centroids and each pixel intensity of image. |
| Step 4: Find the minimum difference from that four difference values. |
| Step 5: Cluster the pixels based on minimum distance of their intensities from the centroid intensities. |
| Step 6: Repeat the steps from step 3 to step 5 for all pixel intensities of input image. |
| Draw backs of existing method: |
| • These methods are less effective and it has greater robustness to noise. |
| • The thresholding is not suitable to produce an optimal value. |
| • Difficult to measure the cluster quality. |
| • It is not suitable for all lighting condition of images. |
Proposed System |
| Mammogram Image Classification for Cancer diagnosis based on |
| • Cancer detection using biclustering method |
| • Wavelet transform based Gray level statistical Features |
| • Probabilistic Neural Network for Image classification |
| The system includes the following methodologies |
| • Image Segmentation for Cancer Detection |
| • Discrete Wavelet Transform |
| • Gray level Co occurrence Matrix Features |
| • PNN Training and Classification |
Advantages |
| • It can segment the cancer regions from the image accurately. |
| • It is useful to classify the cancer images for accurate detection. |
| • Early stage Detection of cancer from images. |
Requirement Specification |
Software Requirement |
| • MATLAB 7.5 and above versions |
| • Image Processing Toolbox |
Hardware Requirements |
| • Pentium(R) D CPU 3GHZ |
| • 1 GB of RAM |
| • 500 GB of Hard disk |
SYSTEM DESIGN |
Block Diagram: |
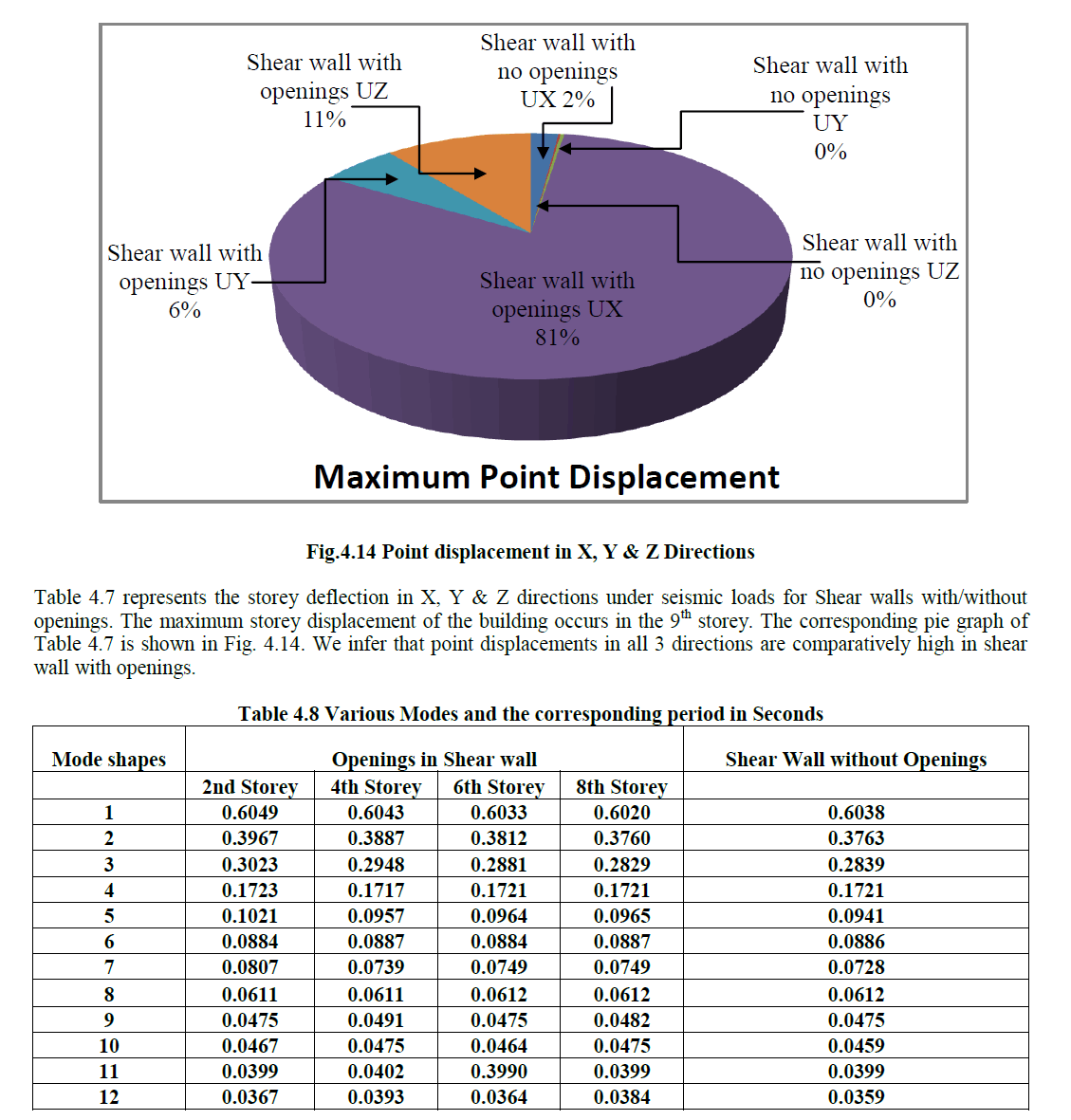 |
Overview: |
| • The system is designed for automatic breast cancer image classification based on segmentation and neural network and these modules follows different methodologies to produce result. |
| • The automatic image classification module includes the feature extraction through wavelet transform and classification by probabilistic neural network after the image segmentation. |
| • The breast cancer region is segmented by using optimal threshold detection in the frequency domain of an input image. The smoothing details from the input are separated by wavelet filter and then threshold is determined to extract the cancer. |
| • The discrete wavelet transform will be used to decompose the segmented image into four subbands and the statistical features are extracted from the high frequency coefficients after cooccurrence matrix analysis and these subbands are contained the detailed coefficients ie., edge information. |
| • Database will be created for non knowledge based image classification and this having same set of normal and abnormal image for training process. |
| • The neural network will used as an image classifier and before that it will be trained with wavelet based glcm features of reference image and target vectors for automatic image classification. |
| • The trained network will classify the image into either normal or abnormal image according input image feature vectors. |
| • This module will be classified the input image into either normal or abnormal images effectively. |
SYSTEM IMPLEMENTATION |
Functional Modules |
Biclustering |
| It is an algorithm used here to identify an abnormal region from an image. It belongs to a distinct class of clustering algorithms that perform synchronous row-column clustering. Biclustering algorithms have also been proposed and used in some application fields such as co-clustering, bidimensional clustering, two-mode clustering and subspace clustering. Biclustering is an important technique in two way data analysis. Biclustering is an extremely useful data mining tool used for identifying patterns, where different genes are correlated based on the subset of conditions in the gene expression dataset. This methodology is effectively applied to extract finer details about the behaviour of genes under certain experimental samples. Thus biclustering can be very well used for detecting cancer. |
Process Flow |
 |
 |
 |
References |
|