ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Sadia Anwar1, Mustafa Kamal1, Arif-Ul-Islam2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In accelerated life testing researcher generally use a life stress relationship between life characteristic and stress to estimate the parameters of failure time distributions at use condition which is just a re-parameterization of original parameters but from statistical point of view it is easy and reasonable to deal with original parameters of the distribution directly instead of developing inference for the parameters of the life stress relationship. By assuming that the lifetimes at increasing stress levels forms a geometric process one can easily handle the original parameters of life distribution directly in accelerated life testing. In this paper a mathematical model for the analysis of constant stress accelerated life testing by using geometric process for Marshall-Olkin Extended Exponential distribution is developed. The estimates of parameters are obtained by using the maximum likelihood method for complete data. In order to get the asymptotic variance of the ML estimator, the Fisher information matrix is constructed. The asymptotic interval estimates of the parameters are then obtained by using this asymptotic variance. In the last a simulation study is performed to illustrate the statistical properties of the parameters and the confidence intervals
Keywords |
| Maximum Likelihood Estimation; Reliability Function; Fisher information Matrix; Confidence Intervals; Simulation Study. |
INTRODUCTION |
| Nowadays many manufactured products have a long life when using them at normal operating conditions due to their good manufacturing designs. As in life testing experiments, the time-to-failure data obtained under normal operating conditions is used to quantify the product’s failure-time distribution and its associated parameters; therefore, it is very costly and time consuming or may indeed be impossible to perform a life test at normal operating conditions. A solution to such life testing problems is Accelerated Life Testing (ALT) in which the products or materials are tested at higher levels of stress to obtain information quickly on the life distribution or product performance. By this process failures which under normal conditions would occur only after a long testing can be observed quicker and the size of data can be increased without a large cost and long time. Generally three types of stress loadings are applied in accelerated life tests: constant stress, step stress and linearly increasing stress. In constant stress loading products are operated at fixed stress levels throughout the test. In step stress, a specimen is subjected to successively higher levels of stress. At first, it is subjected to a specified constant stress for a specified length of time. If it does not fail, it is subjected to a higher stress level for a specified time. The stress on a unit is increased step by step until it fails. In this type of stress, a specimen undergoes a continuously increasing level of stress. Among all stresses, the constant stress method has been used widely and it is considered more important than other stress testing methods because most products are assumed to operate at a constant stress under normal use and hence mimics the actual use of the products. There are two types of data are obtained from ALT, first is the complete in which failure time of each sample unit is observed or known and second is the censored data in which failure time of each sample unit may not be available or observed. Constant stress ALT has been studied by many authors, for example, Ahmad et al. [1], Islam and Ahmad [2], Ahmad and Islam [3], Ahmad et al.[4] and Ahmad [5] discuss the optimal constant stress accelerated life test designs under periodic inspection and Type-I censoring. Yang [6] proposed an optimal design of 4-level constant stress ALT plans considering different censoring times. Pan et al. [7] proposed a Bivariate constant stress accelerated degradation test model by assuming that the copula parameter is a function of the stress level that can be described by the logistic function. Walkins and johns [8] considered constant stress accelerated life test based on Weibull distribution with constant shape and a log linear link between scale the stress factor which is terminated by a Type-II censoring regime at one of the stress level. The geometric process (GP) is first studied by Lam [9] in the problems of repair replacement. Lam [10] studied the geometric process model for a multistate system and concluded a replacement policy to minimize the long run average cost per unit time. Huang [11] introduced the GP model for the analysis of ALT with complete and censored exponential sample under constant stress. Kamal et al. [12] used the GP model for the analysis of ALT with complete Weibull failure data under constant stress. Kamal [13, 14] extended GP model in ALT for type-I and type-II censored Weibull failure data. Kamal et al. [15] implemented the GP model to estimate the parameters of Pareto distribution in ALT. Zarrin et al. [16] investigated the statistical properties of Inverted Weibull Distribution in ALT using GP. Saxena et al. [17] proposed ALT model for Log-Logistic distribution using GP in case of Censored Data. In this paper a mathematical model for the analysis of constant stress ALT using GP for MOEE distribution is developed. ML method of estimation is implemented to obtain the estimates of model parameters. In addition the asymptotic confidence intervals are also generated by using fisher information matrix. The common statistical properties of parameters are inspected by a simulation study. A detailed discussion over the present model and some conclusions arise here are given in the end. |
II. MODEL DESCRIPTION |
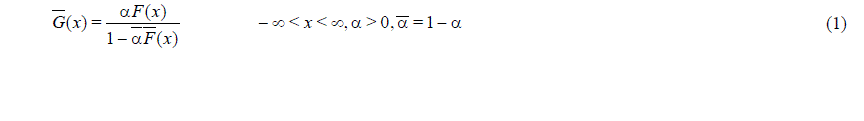 |
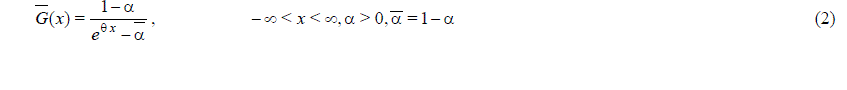 |
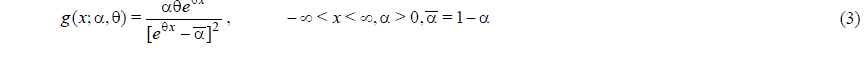 |
 |
 |
VI. SIMULATION STUDY |
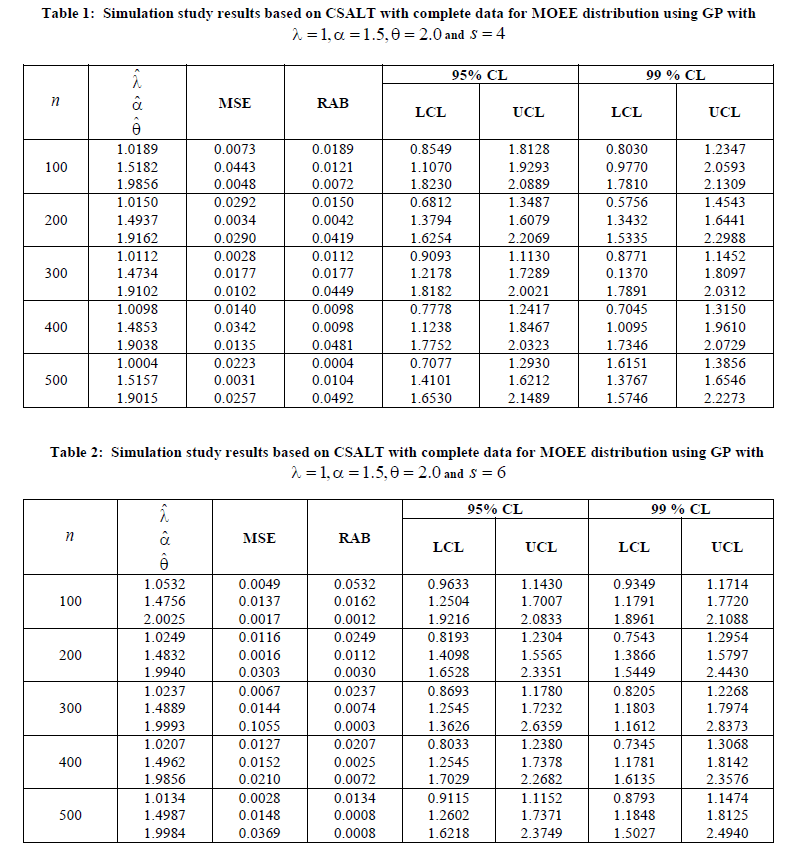
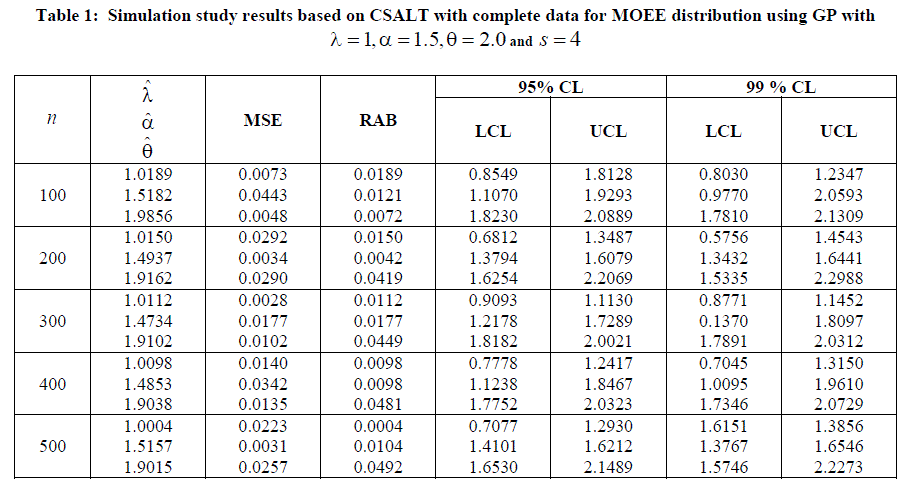
| In order to obtain MLEs of ,and to study the properties of these estimates through Mean squared errors (MSEs), relative absolute biases (RABs) and confidence limits for 95% and 99% asymptotic confidence interval, a simulation study is performed. For this purpose, first different random samples with sizes n ïÃâ¬Ã½100,200,...,500are generated from MOEE distribution. The combinations (,) of values of the parameters are chosen to be (1.0,1.5,2.0) and (1.25,0.5,2.5) . The number of stress levels s is assumed to be 4 and 6 throughout the study. For different sample sizes and stress level, MLEs, MSEs, RABs and the lower and upper CI limits of 95% and 99% confidence interval of parameters based on 500 simulations are obtained by our proposed model and summarized in Table 1, 2, 3, and 4. |
 |
 |
VII. DISCUSSION AND CONCLUSION |
| This paper deals with use of GP model in the analysis of CSALT plan for MOEE distribution with complete data. The MLEs, MSEs and RABs of the model parameters were obtained. Based on the asymptotic normality, the lower and upper CI limits of 95% and 99% confidence interval of the model parameters were also obtained. From the results in Table 1, 2, 3 and 4, it is easy to find that estimates of and perform well. For fixed and we find that as sample size n increases, MSEs, RABs and the confidence intervals get narrower. This is very usual because big samples increase the efficiency of the estimators. From these results, it may be concluded that the present model work well for complete data. |
ACKNOWLEDGMENT |
| This work has been funded by University Grant Commission under Maulana Azad National Fellowship. |
References |
|