ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
G. Manjunatha1, K.S.Basavarajappa2,V.K.Katiyar3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Mathematical model on the industrial pollution and spread of infection diseases using population growth model for epidemic has been studied. Epidemics have ever been a great concern of human kind and we are still moved by the dramatic descriptions that arrive to us from the past, as in Lu-cretius's sixth book of "De RerumNatura" or as in other more recent descriptions that we find in the literature. The "Black Death", the plague that spread across Europe and from 1347 to 1352 and made 25 millions of victims, seems to be far from our lives, but more recent events remind us that epidemics are an actual problem for health institution that are continuously facing emerging and reemerging diseases.The model presented in terms of ordinary differential equations have been studied to investigate the long term effect of population in terms of spread of diseases based on working environment, social and other effects.
Keywords |
| infection, epidemic occlusion,pollution . |
INTRODUCTION |
| The effect of industrial pollution on the surrounding vegetarian and life can always be determined by estimating the extent of pollution in a given industrial domain or land area, the pollution may be in terms of chemical, biological gases and polluted land and water resources. In addition to above types of pollutants there are many indirect pollutants in industrial habituate areas which also cause health hazards. The affected population becomes prone to catch viral and bacterial infections and is susceptible for uniform in the entire industrial population. Mathematical study of the infections diseases including epidemics is mostly confined to homogeneous population consisting of single group [1][2]. The population model are concerned we have considered and analysed biological populations with two or more compartments in the same species. The same model is carried out to investigate on the effect of human population. |
II. MATHEMATICAL MODEL |
| The basic elements for the description of infectious diseases, have been the three epidemiological classes of susceptible, infectiveand removedindividuals, respectively defined as those individuals who are healthy and can be infected; those individuals who are infected and are able to transmit the disease;those individuals who are immune because have been infected and now have recovered;Thus the basic variables identifying the state of the population in the epidemiological perspective are S(t) the number of susceptible at time t,I(t) the number of infective at time t R(t) the number of immune at time t For the epidemic model the following assumptions can be made i) The rate at which members become infective is propositional to the product of the member of susceptibles and the numbers of infectives. ii) The population is closed with no births no deaths except from the disease and no migration. iii) The rate of passage from infective to removed class through recovery or death is propositional to the number of infectives. |
 |
| Moreover, the removal rate R(t) is usually assumed to be a constant indeed, the epidemiological classes characterizing a disease may be morethan these, but considerable insight into the phenomena can however be achieveon the basis of the above description.After the basic state variables introduced above, further gross simplificationmay be introduced concerning the disease progression and effect. Namely, abasic distinction may be done between those diseases that impart lifelong immunity and those which do not. The rest case leads to the so called SIR type model, the second to SIS type models. In fact, the individual path through.In the set of equations (1) The values of parameters will depends on the following assumptions a) Every individual who contracts the diseases is immediately capable of communicating it to others |
| p(t) = { s(t) I(t) R(t)}(2) |
| where p(t) is the population composition vector which contains the relevant information on the composition of the population at time t. |
| b) The population of the fixed size which gives an equation |
| S(t) + I(t) + R(t) = n (constant ) (3) |
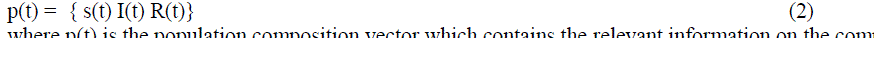 |
| Considering equation (3) as S + I + R = n, the total population size is constant. The equations are (1) to (4) are hold good for the infected one then we can take that the average number of contacts are sufficient to transmit infection per infective in unit time is constant. The number of time such contacts in unit time is I then each constant with susceptible one can be taken as s/kthe infection rate is S I with k equation (4) are the modified equations of Kermac and mc Kendrick [6]. The basic concept of epidemiology is the existence ofthresholds. The value of thresholds are responsible for quantification of the effective parameters such as contact number, population size or vector density that must be exceeded in order for an epidemic to occur or for a disease to remain epidemic. The rate of growth of the infected sub population is propositional to the number of contacts per unit time between of groups S and I then ds |
 |
 |
IV. CONCLUSION |
| Mathematical modelling on industrial pollution and spread of infection disease using population growth model for epidemics have been studied through a mathematical models described in the equations 1 to 11 are directly related with human population.The whole population is active (instead, for some, diseases either part or all of the removed class does not participate in the mixing), that the contact rate is independent of the size of the active population and that contacts with infectives are equally infective. We note that in (1) the factor I (t) / N(t) stands for the probability that the contacted individual is infective. Also,assumption (3) means that the progression of the disease is the same within any infective and ïÃÂç measures the average fraction of recovering individuals in the time unit. With this assumption, a given group of infectives would decrease exponentially with time constant. |
References |
|