ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
R.Muthucumaraswamy1, Tina Lal2 and D.Ranganayakulu3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Laplace transform solution of MHD flow past an incompressible fluid past a uniformly accelerated infinite vertical plate with variable heat and mass transfer, in the presence of rotation has been studied. The plate temperature as well as cocentration level near the plate are raised linearly with time. The velocity profiles, temperature and concentration are studied for different physical parameters. It is observed that the velocity increases with decreasing magnetic field parameter.
Keywords |
| Rotation, accelerated, vertical plate, vertical plat, magnetic field |
INTRODUCTION |
| MHD plays an important role in agriculture, petroleum industries, geophysics and in astrophysics. MHD flow has application in metrology, solar physics and in motion of earth’s core. Also it has applications in the field of stellar and planetary magnetospheres, aeronautics, chemical engineering and electronics. In the field of power generation, MHD is receiving considerable attention due to the possibilities it offers for much higher thermal efficiencies in power plants. |
| Gupta et al [2] studied free convection on flow past a linearly accelerated vertical plate in the presence of viscous dissipative heat using perturbation method. Kafousias and Raptis [3] extended the above problem to include mass transfer effects subjected to variable suction or injection. Free convection effects on flow past an accelerated vertical plate with variable suction and uniform heat flux in the presence of magnetic field was studied by Raptis et al [7]. |
| MHD effects on flow past an infinite vertical plate for both the classes of impulse as well as accelerated motion of the plate was studied by Raptis and Singh[5]. Mass transfer effects on flow past an uniformly accelerated vertical plate was studied by Soundalgekar [10]. Again, mass transfer effects on flow past an accelerated vertical plate with uniform heat flux was analyzed by Singh and Singh [8]. Basant Kumar Jha and Ravindra Prasad[1] analyzed mass transfer effects on the flow past an accelerated infinite vertical plate with heat sources. Singh [9] studied MHD flow past an impulsively started vertical plate in a rotating fluid. Rotation effects on hydromagnetic free convective flow past an accelerated isothermal vertical plate was studied by Raptis and Singh [6]. Recently, Muthucumaraswamy et al [4] studied rotation on MHD flow past an accelerated isothermal vertical plate with uniform mass diffusion using Laplace transform technique. |
| Hence, it is proposed to study the effects of rotation on the hydromagnetic free convection flow of an incompressible viscous and electrically conducting fluid past a uniformly accelerated infinite vertical plate in the presence of variable heat and mass diffusion. The dimensionless governing equations are solved using the Laplace transform technique. The solutions are in terms of exponential and complementary error function. Such a study is found useful in magnetic control of molten iron flow in the steel industry, liquid metal cooling in nuclear reactors, magnetic suppression of molten semiconducting materials and meteorology. |
ANALYSIS |
 |
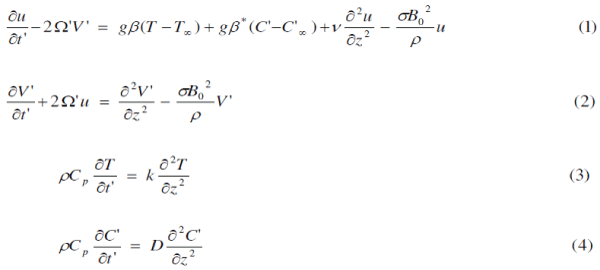 |
| With the following initial and boundary conditions: |
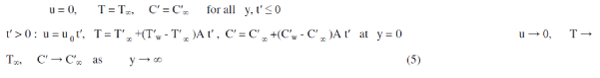 |
| On introducing the following non-dimensional quantities: |
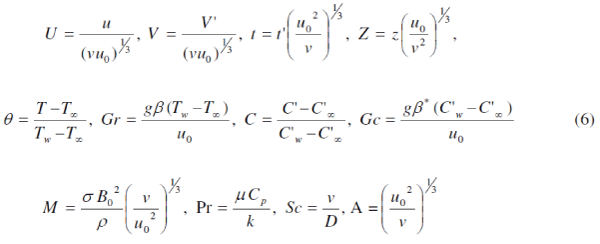 |
| we arrive at |
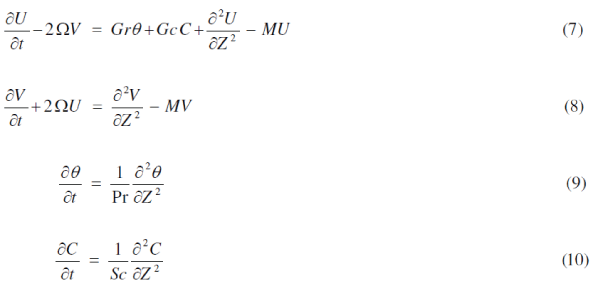 |
| The initial and boundary conditions in non-dimensional quantities are |
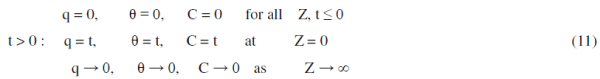 |
| The hydromagnetic rotating free-convection flow past an accelerated vertical plate is described by coupled partial differential equations (7) to (10) with the prescribed boundary conditions (11). To solve the equations (7) and (8), we introduce a complex velocity q = U + iV, equations (7) and (8) can be combined into a single equation: |
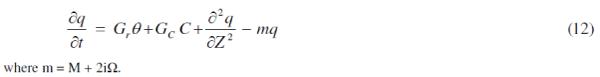 |
Solution Procedure |
| The dimensionless governing equations (9, (10) and (12), subject to the initial and boundary conditions (11), are solved by the usual Laplace-transform technique and the solutions are derived as follows: |
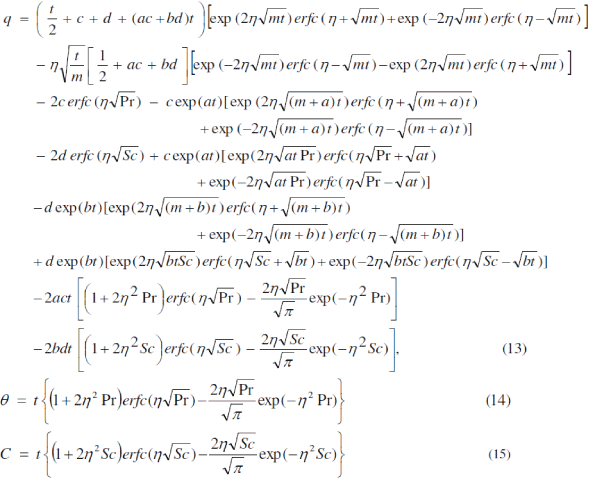 |
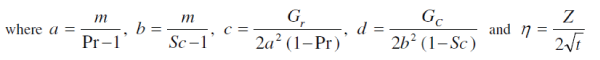 |
| In order to get the physical insight into the problem, the numerical values of q have been computed from (13). While evaluating this expression, it is observed that the argument of the error function is complex and, hence, we have separated it into real and imaginary parts by using the following formula: |
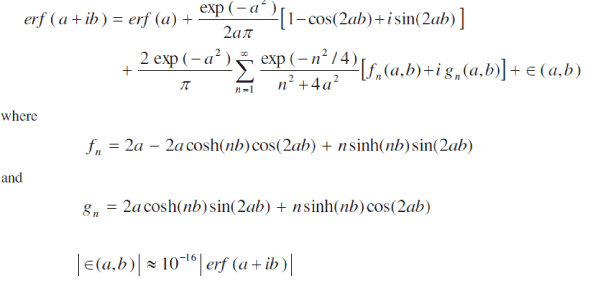 |
RESULTS AND DISCUSSION |
| For physical understanding of the problem, numerical computations are carried out for different physical parameters Gr, Gc, Sc, Pr, m and t upon the nature of the flow and transport. The value of the Schmidt number Sc is taken to be 2.01 which correspond to Ethyl Benzene. Also, the values of Prandtl number Pr are chosen such that they represent air (Pr = 0.71) and water (Pr = 7.0). The numerical values of the velocity, temperature and concentration fields are computed for different physical parameters like Prandtl number, rotation parameter, magnetic field parameter, thermal Grashof number, mass Grashof number, Schmidt number and time. |
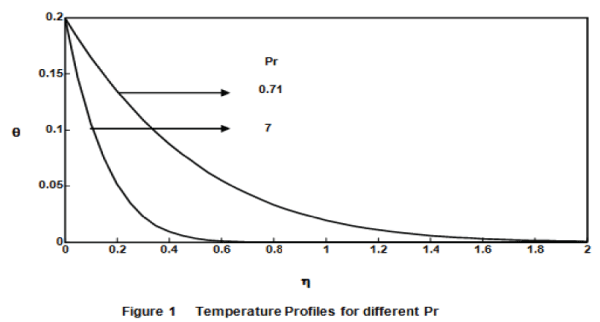
| The temperature profiles are calculated for water and air from equation (14) and these are shown in Figure 1. The effect of the Prandtl number plays an important role in temperature field. It is observed that the temperature increases with decreasing Prandtl number. This shows that the heat transfer is more in air than in water. |
 |
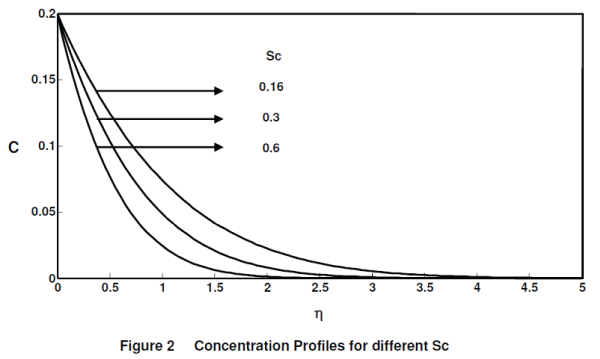
| Figure 2 represents the effect of concentration profiles at time t = 0.2 for different Schmidt number (Sc = 0.16, 0.3, 0.6). The effect of concentration is important in concentration field. The profiles have the common feature that the concentration decreases in a monotone fashion from the surface to a zero value far away in the free stream. It is observed that the wall concentration increases with decreasing values of the Schmidt number. |
 |
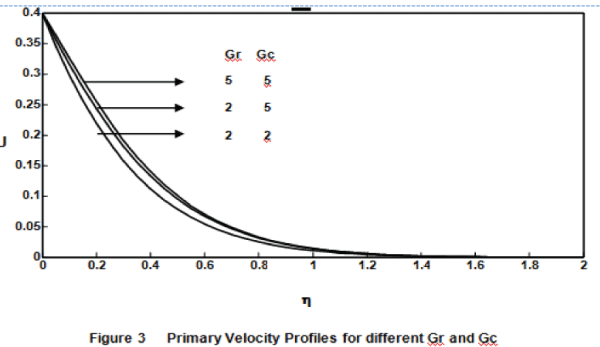
| Figure 3. demonstrates the effects of different thermal Grashof number (Gr =2, 5), mass Grashof number (Gc = 2, 5), M = 5, Ω = 0.5 and Pr = 7, on the primary velocity at time t = 0.4. It is observed that the velocity increases with increasing values of the thermal Grashof number or mass Grashof number. |
 |
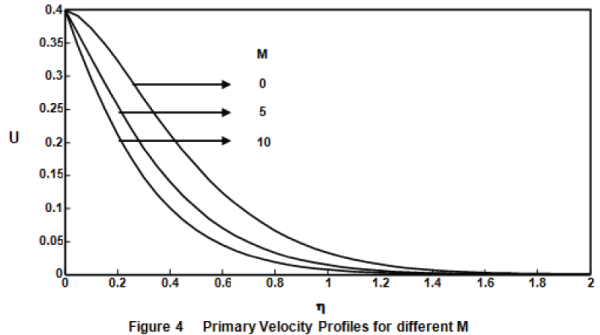
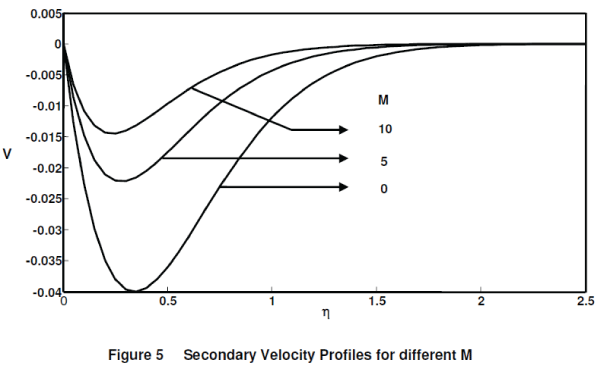
| Figure 4. illustrates the effects of the magnetic field parameter on the velocity when (M = 0, 5, 10), Gr = Gc = 5, Ω = 0.5, Pr = 7 and t = 0.4. It is observed that the velocity increases with decreasing values of the magnetic field parameter. This shows that the increase in the magnetic field parameter leads to a fall in the velocity. This agrees with the expectations, since the magnetic field exerts a retarding force on the free convective flow. The secondary velocity profiles for different magnetic field parameter (M=0,5,10) are presented in figure 5. The trend is just reversed with respect to magnetic field |
 |
| parameter |
 |
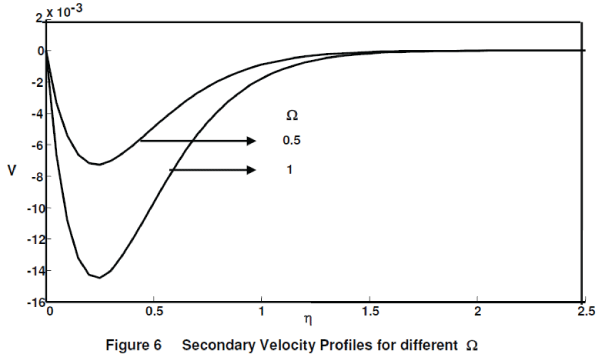
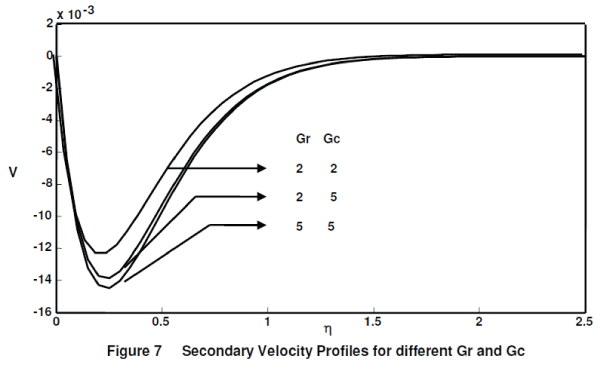
| The secondary velocity profiles for different rotation parameter (Ω = 0.5, 1), Gr = Gc = 5, Pr = 7, M = 10 and t = 0.4 are shown in figure 6. It is observed that the velocity increases with decreasing values of the rotation parameter. The secondary velocity profiles for different thermal Grashof number (Gr = 2, 5), mass Grashof number (Gc = 2, 5), Ω = 0.5, M = 5, Pr = 7 and t = 0.4 are presented in figure 7. The trend shows that the velocity increases with increasing values of thermal Grashof number or mass Grashof number. |
 |
 |
CONCLUSION |
| The closed form solution of rotation effects on unsteady hydromagnetic flow past a uniformly accelerated infinite vertical plate in the presence of variable temperature and mass diffusion has been studied. The effect of different parameters like thermal Grashof number, mass Grashof number and t are studied graphically. It is observed that the velocity increases with increasing values of Gr, Gc and t. But the trend is just reversed with respect to the rotation parameter or magnetic field parameter M. |
References |
|