ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Mittu Mittal1, Gagandeep Kaur2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
“Mixels” are usually the biggest reason for degrading the image quality especially for remote sensing or satellites images. In this paper we present an approach for resolving the mixed pixels by using optimization algorithm i.e. Biogeography based optimization and genetic algorithm. The hybrid approach is used for resolving super pixel problem. This paper deals with the comparison of hybridization of BBO & GA with previously published paper results which are discussed in section V.
Keywords |
| Biogeography based optimization, Evolutionary algorithms, mixed pixel, Migration, Mutation, Remote Sensing, PSNR, and Standard Deviation |
INTRODUCTION TO REMOTE SENSING |
| Remote sensing is the practice of deriving information about the earth's land and water surfaces using images acquired from an overhead perspective, using electromagnetic radiation in one or more regions of the electromagnetic spectrum, reflected or emitted from the earth's surface. This definition certainly does not cover all areas (e.g. meteorological or terrestrial remote sensing), it does serve well as a description of remote sensing. Remote sensing makes use of electromagnetic radiation. The strongest and best-known source of electromagnetic radiation is our sun, which emits radiation over the entire electromagnetic spectrum see fig 1. Besides this natural source of illumination, which is used for passive remote sensing, it is also possible to use an artificial source of electromagnetic radiation, in which case we speak of active remote sensing. |
 |
BIOGEOGRAPHY BASED OPTIMIZATION |
| Biogeography is the study of the distribution of biodiversity spatially and temporally. Over real ecological changes, it is also tied to the concepts of species. Immigration is the introduction of new people into a habitat or population. It is a biological concept and is important in population ecology. A habitat (which is Latin for "it inhabits") is an ecological or environmental area that is inhabited by a particular species of animal, plant or other type of organism. It is the natural environment in which an organism lives, or the physical environment that surrounds (influences and is utilized by) a species population. Biogeography unfolds the geographical distribution of biological organisms. Their interest was primarily focused on the distribution of species among neighboring islands. The application of biogeography to engineering is similar to what has occurred in the past few decades with genetic algorithms (GAs), neural networks, fuzzy logic, particle swarm optimization (PSO), and other areas of computer intelligence. The term “island” here is used descriptively rather than literally. That is, an island is any habitat that is geographically isolated from other habitats. We therefore use the more generic term “habitat” in this paper (rather than “island”). Geographical areas that are well suited as residences for biological species are said to have a high habitat suitability index (HSI). Features that correlate with HIS include such factors as rainfall, diversity of vegetation, diversity of topographic features, land area, and temperature. The variables that characterize habitability are called suitability index Variables (SIVs). SIVs can be considered the independent variables of the habitat, and HSI can be considered the dependent variable. Habitats with a high HSI have many species that emigrate to nearby habitats, simply by virtue of the large number of species that they host. We call this approach to problem solving biogeography-based optimization (BBO). |
GENETIC ALGORITHM |
| Genetic Algorithm GA is an evolutionary based stochastic optimization algorithm with a global search potential proposed by Holland in 1975. GAs is among the most successful class of algorithms under EAs which are inspired by the evolutionary ideas of natural selection. They follow the principles of Charles Darwin Theory of survival of the fittest. However, because of its outstanding performance in optimization, GA has been regarded as a function optimizer. Algorithm begins by initializing a population of solution (chromosome). It comprises representation of the problem usually in the form of a bit vector. Then for each chromosome evaluate the fitness using an appropriate fitness function suitable for the problem.Based on this, the best chromosomes are selected into the mating pool, where they undergo cross over and mutation thus giving new set of solutions (offspring). Genetic algorithms are an optimization technique used in image segmentation. It mimics natural selection, allowing an algorithm to adapt. Solutions are represented by a population of individual chromosomes, usually represented as binary strings. A chromosome is made up of genes, each of which can represent a particular characteristic. Each individual in the population is evaluated and given a fitness score based on how well they solve the particular problem. Higher the individual’s fitness score, the greater their probability of breeding. Breeding creates the next generation through crossover and mutation. Crossover combines the chromosome of two individuals, creating a new individual which is unlike either of the parents. Mutation, which occurs only a small percent of the time, randomly alters a new individual’s chromosome. Since the more optimal individuals have a greater chance of breeding, the population tends to evolve and reach an optimal solution. |
| A. Working Principle of GA |
| GA begins with a set of solution (represented by chromosomes) called the population. Solution from one population are taken and used to form a new population. Solutions are selected according to their fitness to form new solutions (offspring/ children). This is repeated until some condition is satisfied like no. of population or improvement of the best solution). |
| 1. [START] Generate random population of n chromosomes i.e. suitable for the problem. |
| 2. [FITNESS] Evaluate the fitness f(x) of each chromosome x in the population. |
| 3. [NEW POPULATION] Create a new population by repeating following steps until the new population is complete. |
| (a) [SELECTION] Select two parent chromosomes from the population according to their fitness (better the fitness, bigger the chance of selection). |
| (b) [CROSSOVER] with a crossover probability, cross over the parents to form new children. If no cross over was performed, children is the exact copy of his parents. |
| (c)[MUTATION] with a mutation probability, mutate new children at each locus (position in chromosome). |
| (d) [ACCEPTING] place new offspring in the new population. |
| 4. [REPLACE] use new generated population for the further run of the algorithm. |
| 5. [TEST] if the end condition is satisfied then stops and returns the best solution in current population. |
| 6. [LOOP] Go to step 2. |
| B. MIXED PIXEL PROBLEM |
| The importance and impact of spatial resolution is also witnessed by the mixed pixel ‘problem’. Mixed pixels, sometimes known as 'mixels', occur where the image pixels are not homogenous, or ‘pure’. Instead a pixel contains a measure of the energy reflected or emitted from several different materials or land surface objects and the sensor records a composite of these responses (Fig 2). |
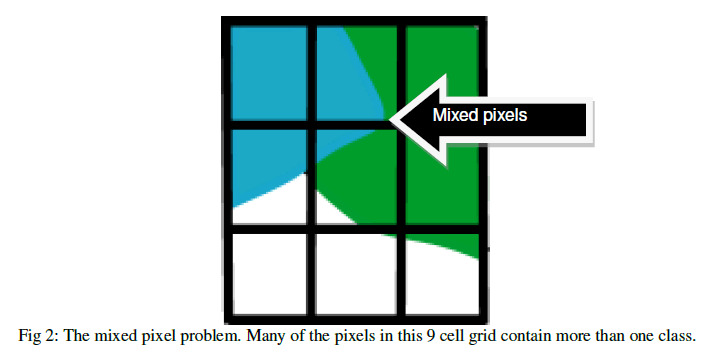 |
| In many cases this spectral mixing can make it very difficult for the image analyst to identify the different sub-pixel fractional components that serve to make up the landscape under observation. Under these circumstances the analyst may wish to employ a finer resolution data set, in order that a greater number of ‘pure’ pixels may be recorded. Even with very fine resolution, however, there is still the issue of edge pixels, where pixels can show the boundaries between different land surface properties. Land surface features do not follow the arbitrary confines of the pixel and therefore even very fine spatial resolution data of the order of a few meters’ will still experience some degree of confusion and spectral missing. |
| As you can imagine, mixed pixels can cause great difficulties in the stages of image analysis and interpretation. One of the common tasks in this process is image classification. Classification is widely used as it allows users to easily discriminate information from images presented as a series of categories (classes) rather than raw digital number (DN) values. Images are classified on the basis of their spectral properties. Each pixel of remote sensing image contains the information from multifarious ground objects due to the difference from the resolution of remote sensing image, called Mixed pixel. |
METHODOLOGY |
The proposed algorithm can be informally described with the following steps: |
| ïÃâ÷ Read a remote sensing image from our data base. |
| ïÃâ÷ Initialize the basic parameters i.e. pm (Mutation Probability), n (No. of sets to be created), Gen limit (No. of generations), N (Population Size), Lambda (Immigration Ratio) and then read the data and extract the valuable information. |
| ïÃâ÷ Set a threshold value i.e. maximum value. So that appropriate value can be calculated. |
| ïÃâ÷ Calculate the best fitness value using BBO by splitting the image into rows and columns. |
| ïÃâ÷ After that Crossover and mutation is done using GA for declaring the calculated fitness value as best value. |
| ïÃâ÷ Then restore the image and calculate the parameters i.e. standard deviation, PSNR. |
| ïÃâ÷ Repeat till all the mixed pixels are resolved. |
RESULTS AND DISCUSSION |
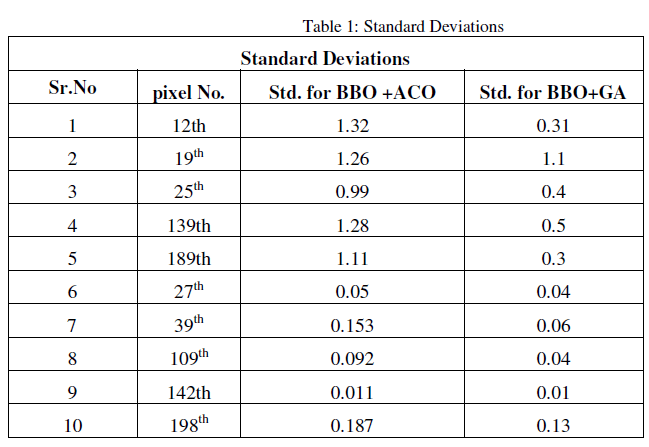
| In this thesis the performance of BBO and GA algorithm is analysed for mixed pixel resolution in satellite images by hybridization of both these algorithms. Performance analysis of algorithms is done by using various operators of both these algorithms. Implementation is done in MATLAB 2010. The results of this thesis are shown below in table 1. The below table 1shows the calculated standard deviations of both algorithms i.e. BBO & ACO (Ant Colony optimizatioin algorithm) and BBO & GA. |
 |
| Below Figure 3 shows bar graph of these calculated values of Alwar region image. This Graph clearly depicts the results of the thesis. |
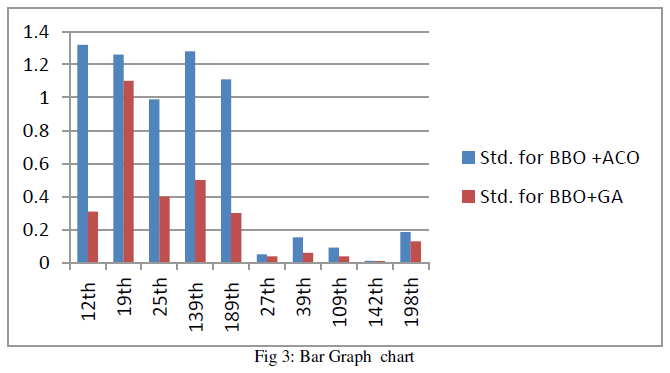 |
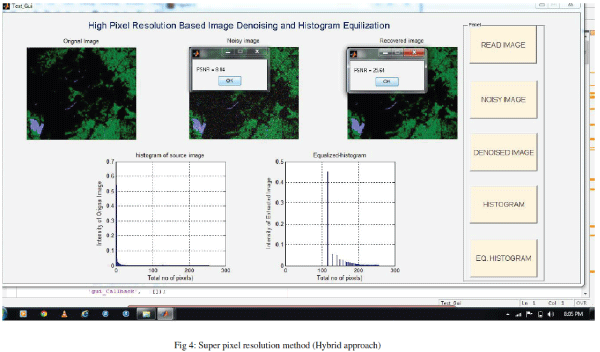
| This bar graph clearly depicts the change in the value of standard deviation of both algorithms. The blue line shows the standard deviation of the previously implemented algorithm i.e. Fusion of biogeography based optimization and ant colony optimization. The red line shows the value of standard deviation of the proposed algorithm i.e. hybridization of biogeography based optimization algorithm & genetic algorithm. Below Figure 4 is shown the complete high pixel resolution method of Denoising. In this way with the use of hybridization approach i.e. BBO & GA we can denoise the image up to maximum extent and resolving mixed pixels problem in efficient manner for improving its quality of output image. |
 |
CONCLUSION & FUTURE SCOPE |
| As Concluded mixed pixel is a big problem in any remotely sensed imaging or high resolution image. Remote Sensing is the gathering of information concerning the earth’s surface that do not involve contact with the surface or object under study. Thus our proposed methodology i.e. Hybridization of BBO & GA can resolve greater number of mixed pixels problem in effective way and also helpful in providing great accuracy in output images. , it is clear that the PSNR value of our proposed algorithm is very less as compared to traditional method of image denoising. So our proposed methodology of resolving mixed pixels is very effective approach. This methodology improves the quality of image upto 70 to 80 percent depends on the resolution of image as compared to original. Therefore BBO can better to detect mixels in remote sensing images. |
| Future work will focuses on combining these optimization algorithms to other algorithms like ANN’s, Fuzzy algorithms to resolve mixels problem. Our proposed Methodology will also serve as bases for many other engineering disciplines like Environmental assessment and monitoring , Nonrenewable resource exploration (minerals, oil, natural gas),Renewable natural resources (wetlands, soils, forests, oceans),Meteorology (atmosphere dynamics, weather prediction),Mapping (topography, land use), Military surveillance and reconnaissance (strategic policy, tactical assessment), News media (illustrations, analysis). |
ACKNOWLEDGEMENT |
| This study was supported by the Department of computer science & Engineering of RIMT Institutes Near Floating Restaurant, Sirhind Side, Mandi Gobindgarh-147301, and Punjab, India. |
References |
|