ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
S.Vadivazhagi1, Dr.N.Jaya2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
This paper describes the controller design of non linear system.The Non linear system taken up for the study is the Interacting Conical Tank Systems.In this paper, design of controllers based on Skogestad tuning is determined.For each stable operating region, a first order process model is identified using Process reaction curve method.The control is done and the responses for different operating regions are taken.Simulation is made by the MATLAB software.
Keywords |
| Non Linear System, Mathematical Modelling,Interacting Conical Systems,Skogestad PI controller |
INTRODUCTION |
| In most of the industries chemical process present many challenging problems due to their nonlinear dynamic behaviour.Because of inherent non linearity,most of the chemical process industries are in need of traditional control techniques.One such non linear process taken up for study is Interacting Conical systems[1]. |
| Conical tanks are best suited for food process industries, concrete mixing industries, hydrometallurgical industries and waste water treatment industries. Its shape contributes to better drainage of solid mixtures, slurries and viscous liquids. To achieve a satisfactory performance using conical tanks, its controller design becomes a challenging task because of its non - linearity. This non - linearity arises due to its shape. It is broad at the end and becomes narrow in the lower end[10]. The primary task of a controller is to maintain the process at the desired set point and to achieve optimum performance when facing various types of disturbances . |
| Conventional controllers are widely used in industries since they are simple,robust and familiar to the field operator.Practical systems are not precisely linear but may be represented as linearized models around a nominal operating point[4]. |
| The work in this paper is divided in two stages. 1) Mathematical Modelling 2) Skogestad controller Implementation. A Mathematical model is developed for Two Tank Conical Interacting system using the Mass Balance Equation.The operating parameters of the process is given in a table from which the Open loop response of the process is obtained. Piecewise Linearization is carried out.The controller tuned using Skogestad method named after the originator is based on the direct method.The objective of the paper is to show that by employing the proposed tuning of PI controllers,an optimization can be achieved[2]. |
| The Proportional Integral(PI) and Proportional-Integral-Derivative(PID) controllers are widely used in many industrial control systems for several decades.S.Nithya et al.[1] discussed about the control issues associated with the non linear systems in real time using cost effective data acquisition system.The limitations of a PI controller for a first order non linear process with dead time was discussed by R.Anandanatarajan et al.[2].D.Dineshkumar et al.[4]. implemented Skogestad PID controller for Interacting Spherical Tank System.Simulation studies were carried out for this non linear process.Sigurd Skogestad[5] proposed the best simple tuning rules in the world.The analytical tuning rules are as simple as possible and still result in a good closed-loop behaviour.A Neuro based model reference Adaptive control of a conical tank level was proposed by N.S.Bhuvaneswari et al.[6]. |
| Paper is organized as follows. Section II describes the Mathematical Modelling of Two Tank Conical Interacting Systems and its operating parameters.Piecewise linearization is carried out around four different operating regions .The implementation of Skogestad PI controller is discussed in Section III. Section IV presents experimental results showing four different simulations for four regions. Finally, Section V presents Conclusion. |
MATHEMATICAL MODELLING OF TWO TANK CONICAL INTERACTING SYSTEM |
| The two tank conical interacting system consists of two identical conical tanks (Tank 1 and Tank 2), two identical pumps that deliver the liquid flows Fin1 and Fin2 to Tank 1 and Tank 2 through the two control valves CV1 and CV2 respectively. These two tanks are interconnected at the bottom through a manually controlled valve, MV12 with a valve coefficient β12. Fout1 and Fout 2 are the two output flows from Tank 1 and Tank 2 through manual control values MV1 andMV2 with valve coefficients β1 and β2 respectively[3]. |
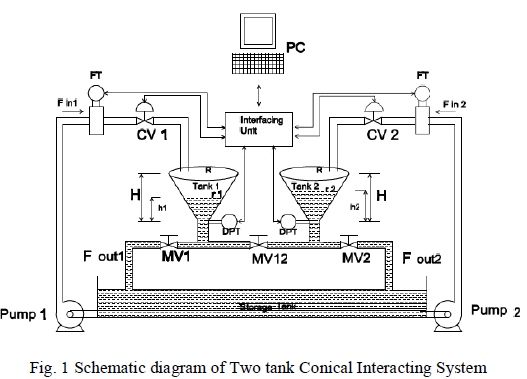 |
 |
| The non linear equations describing the open loop dynamics of the Two Tank Conical Interacting Systems is derived using the Mass balance equation and Energy balance equation principle[9] .The Mathematical model of The mathematical model of two tank conical interacting system is given by [6] : |
| Where |
| A(h1) = Area of Tank 1 at h1(cm2) |
| A(h2) = Area of Tank 2 at h2(cm2) |
| h1= Liquid level in Tank 1 (cm) |
| h2= Liquid level in Tank 2 (cm) |
| The open loop responses of h1 and h2 are shown below: |
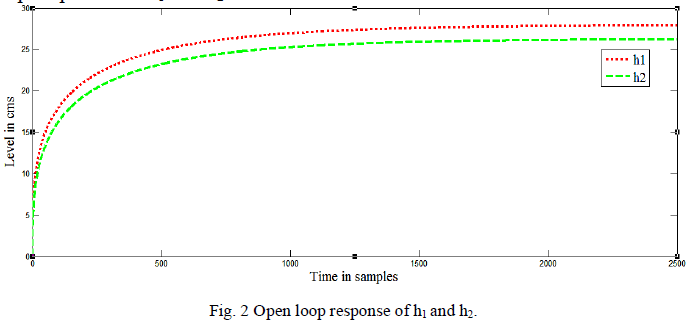 |
| The process considered here has non linear characteristics and can be represented as piecewise linearized regions around four operating regions. |
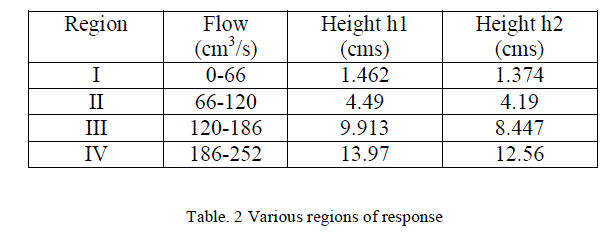 |
IMPLEMENTATION OF SKOGESTAD PI CONTROLLER |
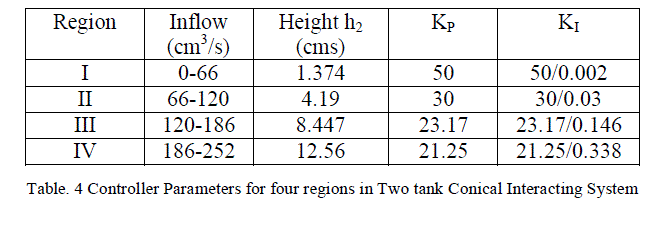
| Transfer function for every region is obtained by substituting the values of time constant and gain using Process reaction curve method[7].Transfer functions for different regions are represented in Table II. PI controller is designed based on Skogestad method [5]. |
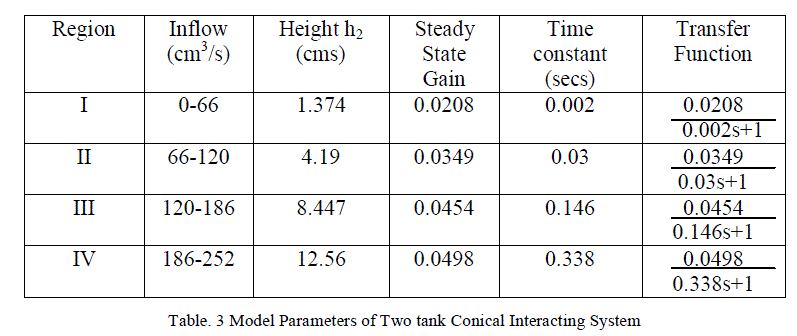 |
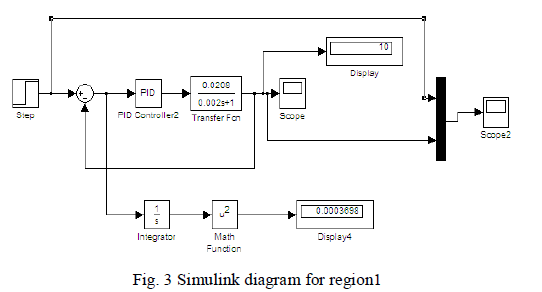
| PI controller is designed for all the four regions based on Skogestad method.Figure 3 represents the simulink diagram of PI controller for region I using Matlab[4] and it also depicts the blocks used to find error indices.Similarly the Process is simulated for different regions and the responses obtained with and without disturbances are discussed in section IV. |
 |
 |
SIMULATION RESULTS |
| The simulation is carried out using MATLAB.First the non linear response of Two Tank Conical Interacting Systems is linearised into four regions and the optimum PI controller parameters for these four regions is estimated. Figures 4,5,6 and 7 shows the controller response for regions 1,2,3 and 4 with and without disturbance. |
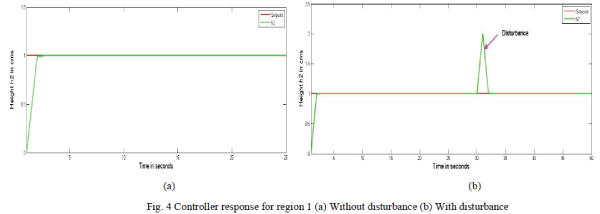 |
| Figure.4. shows the controller response for region 1 (0-66 cm3/s).A set point of 1 is given. The response as shown in Figure 4(a) clearly indicates how the controller takes the action for the given set point. Also the response shown by Figure 4(b) confirms the controller action even in the presence of disturbance so as to reach the desired set point. |
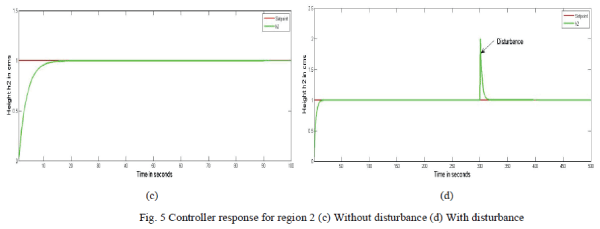 |
| Figure.5. shows the controller response for region 2 (66-120 cm3/s).A set point of 1 is given. The response as shown in Figure 5(c) clearly indicates how the controller takes the action for the given set point. Also the response shown by Figure 5(d) confirms the controller action even in the presence of disturbance so as to reach the desired set point. |
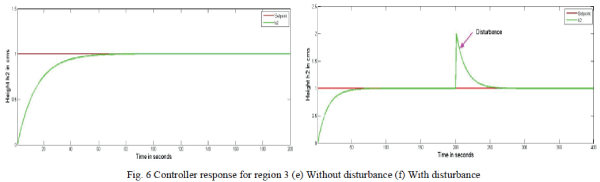 |
| Figure.6. shows the controller response for region 3 (120-186 cm3/s).A set point of 1 is given. The response as shown in Figure 6(e) clearly indicates how the controller takes the action for the given set point. Also the response shown by Figure 6(f) confirms the controller action even in the presence of disturbance so as to reach the desired set point. |
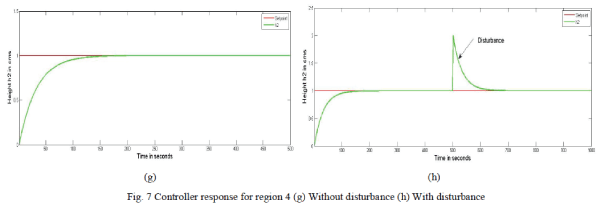 |
| Figure.7. shows the controller response for region 4 (186-252 cm3/s).A set point of 1 is given. The response as shown in Figure 7(g) clearly indicates how the controller takes the action for the given set point. Also the response shown by Figure 7(h) confirms the controller action even in the presence of disturbance so as to reach the desired set point. |
| Skogesad PI controller is implemented on Conical Interacting systems through simulation and the respective servo and regulatory responses were obtained.From the figures it can be inferred that the designed Skogestad PI controller takes the controller action at every region for the given Setpoint even in the presence of disturbance. |
CONCLUSION |
| In this paper, Skogestad PI controller is designed for a Two tank Conical Interacting System.The Simulation results confirm that the controller designed gives satisfactory response for a given set point .Also the controller effectively rejects the disturbance and brings back the output to the desired set point. |
References |
|