ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| K.Sarojini Department of Information Technology, SIES College, University of Mumbai, Sion (west), Maharashtra, India. |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Although there has been a demarcation between development and evolution (maintenance) of software, this is increasingly irrelevant as fewer and very fewer systems are completely new. Additionally, once a software engineer understands a system's structure, it is difficult to preserve this understanding, because the structure tends to change during maintenance. So Software engineers greatly emphasize on good modular structures as well modularized software is easier to develop and maintain. In this paper, I propose two algorithms, one as a search optimization technique and another as a multiobjective fitness evaluation function of the search technique. The former one, I have labeled as Modified Pareto Optimal Genetic Algorithm (Modified par-op GA) and the later one as Non-Dominance Module Ranking Algorithm (Non-DMR). As the Fitness function is a component of GA, I have embedded the Non-DMR within the Modified par-Op GA.
Keywords |
| Non-hierarchical clustering optimization, cohesion, coupling, reverse engineering, Agglomerative hierarchical clustering, Pareto optimality. |
INTRODUCTION |
| Software architecture is a model of the software system expressed at a high level of abstraction [1]. The architectural view of a system raises the level of abstraction and concentrating on only ‘black box’ elements. Normally, architecture will not be explicitly represented in the code, but it has to be documented. Often, the available documentation is incomplete, outdated or is completely missing, the designers having only the code available, sometimes only in compiled form. So the reverse engineering community has developed lot of techniques and tools to create appropriate abstraction of software structure which makes them more understandable and easier to maintain. Software clustering technique is a key to create these types of abstractions. It follows the emergent of search based approaches to search the similar modules in different clusters. In the search based approach [2] the attributes of a good modular decomposition are formulated as objective, the evaluation of which as a ‘fitness function’ guides a search based optimization. |
| Bunch uses a single objective [3] called Modularization quality (MQ) as a fitness function. It combines the twin objectives of high cohesion and low coupling. Cohesion is a measure of the number of intra edges (edges that lie inside a cluster) while coupling is measured by the number of inter edges (The edges that connect two clusters) in the modularization [4]. For example if functions that access the same variables are placed into the same module, the module would tend to have communicational cohesion. Low coupling and high cohesion as a single objective may yield suboptimal results. This led the researches to find Pareto optimality for automated module clustering within multi-objective [5] paradigm. Two formulation of the multiple objective approach are Maximizing clustering Approach (MCA) and Equal size cluster approach (ECA). In MCA modules will not be put in one cluster and series of isolated clusters will not be produced. The ECA aims to minimize the difference between the maximum and minimum number of modules in a cluster through which we can create equal size clusters. In multi- objective paradigm Genetic algorithm is used as a search algorithm. The above will be discussed detail in section 3 and 4. Although the search based approaches do not guarantee to provide optimal solutions, yet, they can obtain near optimal solutions in reasonable amount of computational time. |
| The rest of the paper is organized as follows. Section 2 describes the background and related study of software module clustering. Section 3 explains the software module clustering as a multi-objective search problem. Section 4 presents Multi-objective genetic algorithm. Section 5 and 6 explains my proposed approach and experimental results with discussions respectively. |
BACKGROUND AND RELATED STUDY |
| Optimization algorithms take an initial solution(module) as a parent and tries to improve this solution by iterative adaptations according to some heuristic. The optimization method has been used to produce both hierarchical [6] and nonhierarchical [7] clustering. A typical nonhierarchical clustering optimization method starts with an initial partition derived based on some heuristic. Then, modules are moved to other clusters in order to improve the partition according to some criteria. This relocating goes on until no further improvement of this criterion takes place. Nonhierarchical method creates one level of clustering. Since only one set of clusters is output, the user normally has to input the desired number of clusters. In hierarchical approach clusters are created in levels actually creating sets of clusters in each level. Hierarchical methods can be subdivided into Agglomerative Hierarchical clustering and Divisive hierarchical clustering. In the former type, each object initially represents a cluster of its own. Then clusters are successively merged until the desired cluster structure is obtained. In the later, all objects initially belong to one cluster. Then the cluster is divided into sub-clusters, which are successively divided into their own sub-clusters. This process continues until the desired cluster structure is obtained. I have used Divisive hierarchical clustering method in outer algorithm for initial clustering. |
| Genetic clustering algorithms are randomized global optimal search heuristic that mimics the process of natural evolution, having large amount of implicit parallelism. Genetic algorithms are characterized by attributes, such as the objective function, the encoding of input data, the genetic operators, such as crossover and mutation, and population size. The first multi-objective GA, called vector evaluated GA (or VEGA), was proposed by Schaffer [8]. Afterwards, several multi-objective evolutionary algorithms were developed including Multiobjective Genetic Algorithm (MOGA) [9], Niched Pareto Genetic Algorithm (NPGA) [10], Weight-based Genetic Algorithm (WBGA) [11], Random Weighted Genetic Algorithm (RWGA)[12], Strength Pareto Evolutionary Algorithm (SPEA) [13], Pareto-Archived Evolution Strategy (PAES) [14], Region-based Selection in Evolutionary Multi-objective Optimization (PESA-II) [15], Fast Non-dominated Sorting Genetic Algorithm (NSGA-II) [16], Multi-objective Evolutionary Algorithm (MEA) [17], and Dynamic Multi-objective Evolutionary Algorithm (DMOEA) [18]. Note that although there are many variations of multi-objective GA in the literature, these cited GA are well-known and credible algorithms that have been used in many applications and their performances were tested in several comparative studies. |
MULTI-OBJECTIVE APPROACH FOR SOFTWARE MODULE CLUSTERING |
| Complex structure of the software is typically depicted by one or more directed graphs called Module Dependency Graphs (MDGs). These graphs can be used to describe the modules (or classes) of a system and their static interrelationship using nodes and directed edges, respectively (see Fig 1). |
| Thus clustering can be visualized as a graph partitioning problem, which is known to be NP hard. It cannot be solved efficiently by traditional optimization techniques and in many real-life problems, objectives (see the bulleted list below) under consideration conflict with each other. Hence, optimizing x (a solution) with respect to a single objective often results in unacceptable results with respect to the other objectives. Therefore, a perfect multiobjective solution that simultaneously optimizes each objective function is almost impossible. A reasonable solution to a multi-objective problem is to investigate a set of solutions, each of which satisfies the objectives at an acceptable level without being dominated by any other solution. In multi-objective software module clustering, multiple objectives will become the following: |
| • The sum of intra-edges of all clusters(maximizing) |
| • The sum of inter-edges of all clusters(minimizing) |
| • Modularization Quantity called as MQ (maximizing) |
| • The number of isolated clusters(Minimizing) |
| The intra-edges are those in which the source and target of the edge lie inside the same cluster. The inter-edges are those for which the source and target lie in distinct clusters [19]. MQ is the sum of Modularization Factor (MFk) which is the ratio of intra-edges and intra-edges in each cluster. Modularization Factor (MFk) for cluster k can be defined as follows [5]: |
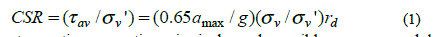 |
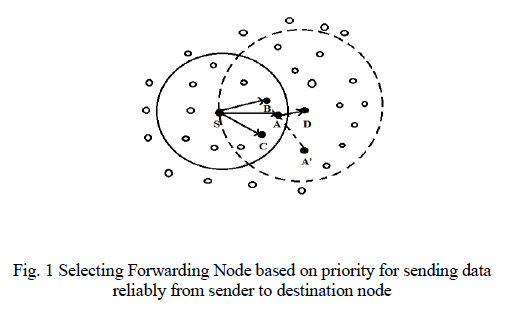 |
| Fig. 2. Non-Dominance solutions selection using Pareto Optimal search. |
| In the Fig 2, I have taken 3 chromosomes (X, Y And Z) from population N. The genomes of each chromosome are encoded using numerals. Z is compared with X and Y taking the similarities as fitness functions. Similarity is expressed using non-dominance property. Pareto optimality determines solution X is better than solution Y to cluster with solution Z. We can observe that, solution X has more similarities with solution Z than solution Y. So Solution Z and X are non-dominant to each other whereas Z dominates Y. |
MULTI-OBJECTIVE GENETIC ALGORITHMS |
| Genetic algorithms use concepts of population and of recombination inspired by Darwinian evaluation. The concept of GA was developed by Holland and his colleagues in the 1960s and 1970s [20]. GA are inspired by the evolutionist theory explaining the origin of species in nature, weak and unfit species within their environment are faced with extinction by natural selection. The strong ones have greater opportunity to pass their genes to future generations via reproduction. In the long run, species carrying the correct combination in their genes become dominant in their population. Sometimes, during the slow process of evolution, random changes may occur in genes. If these changes provide additional advantages in the challenge for survival, new species evolve from the old ones. Unsuccessful changes are eliminated by natural selection [21]. |
| Genetic algorithms operate with a collection of chromosomes called a population. The population is normally randomly initialized. As the search evolves, the population includes fitter and fitter solutions, and eventually it converges, meaning that it is dominated by a single solution. Being a population based approach, GA are well suited to solve multi-objective optimization problems. A generic single-objective GA can be modified to find a set of multiple non-dominated solutions in a single run. The ability of GA to simultaneously search different regions of a solution space makes it possible to find a diverse set of solutions for difficult problems with different objectives. |
PROPOSED APPROACH |
| This section describes our proposed approach. In generic multi-objective optimization approach, all the objectives should be either the minimization objectives or maximization objectives to get optimal solution in single run. But Non-Dominance module ranking algorithm (Non-DMR) does software module clustering without forcefully change minimization objective constraints to maximization or vice versa. A general frame work of Modified Par-Op GA and Non-DMR algorithms is given in Fig.3. |
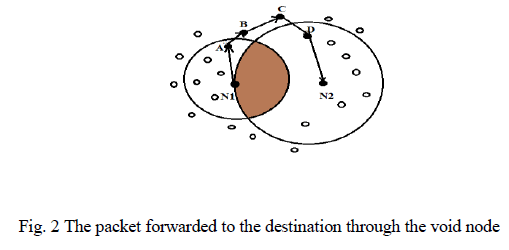 |
| Our proposed algorithm has two different algorithms in which one will be executed within another. The outer algorithm is a modified Par-Op GA which finds nondominant solutions (modules/clusters) using Pareto optimality as a base. This finds whether one solution is better than another (Not how much better) using nondominance property through which initial clustering made. In this, I have used Divisive hierarchical clustering in which all modules initially belong to one cluster. By applying Modified Par-Op GA on that cluster, initial clustering partition has made. The inner algorithm, termed as Non-DMR, is applied separately on each resultant clusters of Modified Par-Op GA. This algorithm finds that, each solution is how much better than the other solution by ranking the each solution with respect to multiple objectives. Highest ranked solution is the worst one to satisfy the multiple objectives. Through ranking, decision maker can exactly group similar modules in one cluster. Additionally, ranking helps to increase the number of clusters. Increasing the number of clusters will also increase the MQ (Modularity Quality) which is one of the maximization objectives in module clustering. Non-DMR can be directly applied on the initial cluster without using Modified Par-Op GA. But it will increase search and computational time in considerable amount. |
EXPERIMENTAL RESULTS AND DISCUSSIONS |
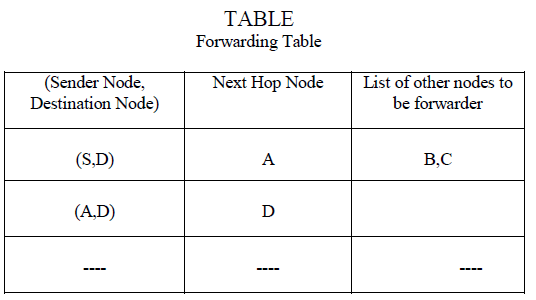
| The effectiveness of the algorithm has been studied on 4 different size real world module clusters and among them i have taken one (mtunis - an operating for educational purposes written in the Turing Language) to explain the execution. Initial clusters (see Table.1) are labelled as C1, C2, C3, C4 and C5. Solutions (modules) are labelled as 1.X, 2.X, 3.X, 4.X. and 5.X. All the modules which are termed as 1.X are non-dominant to each other. Likewise modules 2.X, 3.X, 4.X and 5.X. are non-dominant to each other within them. To apply Modified Par-Op GA initially all the clusters are merged together and considered as one cluster called Pt. Pt has randomly generated N solutions (total number of modules in all clusters). |
 |
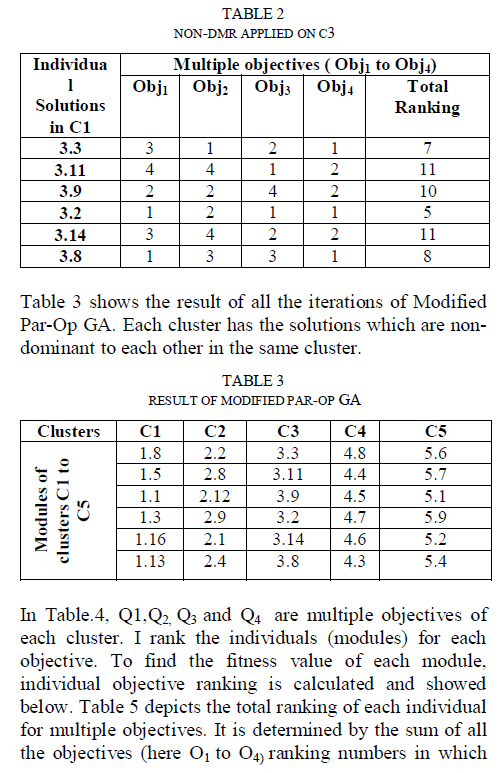
| Then randomly selected module from Pt is compared (non-dominancy) with its remaining modules. For example if we select solution 3.2 to compare with all other solutions, the resultant solution set will be 3.3, 3.11, 3.9, 3.2, 3.14, 3.8 given in Table 2.. These solutions will be moved to one separate cluster called C3. Though it seems finding optimal solutions by comparing one solution with all other solution is a tiring search, we yield a cluster of solutions (not a single solution) in a single run. Now we have two clusters, C3 which has only 3.X solutions and Pt which has other than 3.X. |
| In a multi-objective problem a single fitness value can only be obtained if the objectives are grouped into a single utility function. This is not appropriate since a specific set of weight values drives the GA towards specific solutions. After completed one iteration of Modified Par-Op GA, the inner algorithm, Non-DMR starts to execute taking the result of first iteration (here C3) as an input. The individuals in the cluster C3 indicated by 3.3…3.8 are ranked for each objective. Here we determine the worst individual(s) (modules) in the group (cluster) by ranking the individuals for each objective (such as high cohesion and low coupling) and selecting the individual(s) with the worst total ranking (see Table 2, below). The lower rank number, here 5 of solution 3.2, indicates a better value for the objective being considered. Same rank numbers are assigned to individuals with equal or similar objective values. The total ranking for each individual is then determined by the sum of all the ranking numbers. The individual(s) with the highest total rank, here 3.11 and 3.14, are replaced by the offspring in the population and put in another cluster called C33. Using ranking as a way to determine the worst individual in a group allows good individuals for specific objectives to evolve as well as individuals that are average in two or more objectives. Table 2 shows the result derived from first iteration of Non-DMR. |
 |
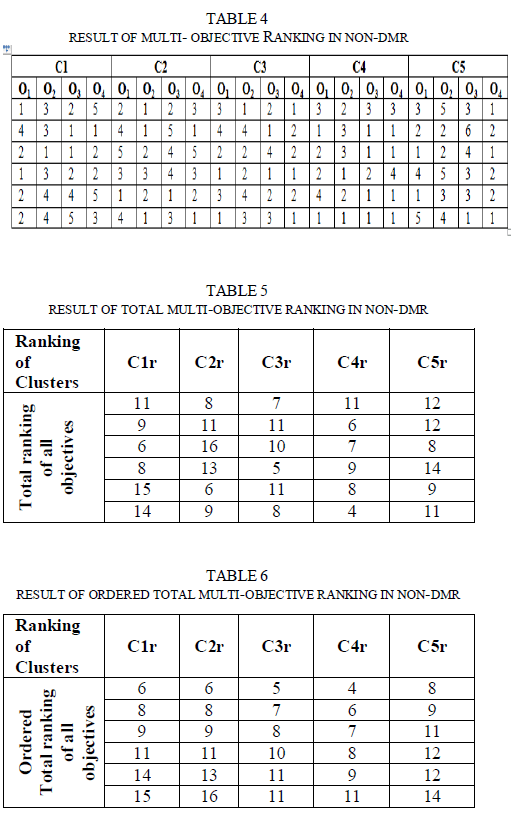
| we get single ranking number for each module. In table 5 ranking are not in sequence. |
| In Table 6, since the ranking numbers are ordered in ascending, the worst individuals comes bottom of the search space which reduces the search to select those individuals. Fitness of individuals is implicitly given by their objective values and their rank against others. There is an explicit fitness function in this problem to replace the worst individuals from its native cluster. Individual(s) (modules) which have the ranking numbers greater than On*3 (On is the total number of objectives (here On = 4 and On*3 = 12)) are worst individual(s) to be removed and replaced to new cluster. The C1r in the Table 6, modules 1.13, 1.16 (refer Table 3 to identify corresponding module names) which have been ranked as 14 and 15(greater than 12) are worst modules. They move to new cluster termed C11, given in Table 7. |
 |
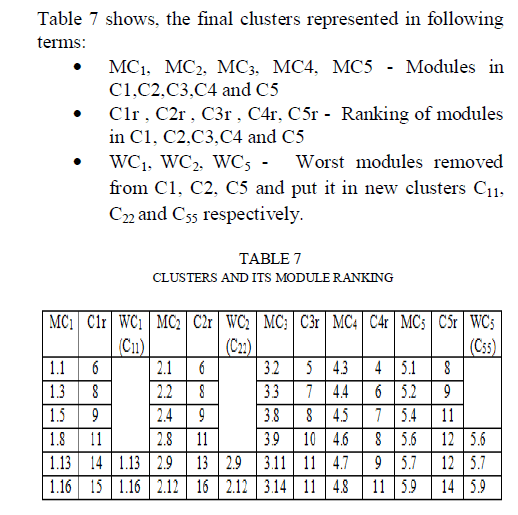 |
| Clusters C3 and C4 do not have worst modules because of all modules have ranking below 12.Finally, we have 8 clusters C1 to C5, C11, C22, and C55 which have lowest possible coupling, highest possible cohesion within modules, good MQ ratio and zero isolated clusters (Taken 4 objectives) within the reasonable number of search and acceptable amount of computational time. Additionally, since the objectives are not specified it is flexible to add more number of objectives as per decision maker’s requirements. |
CONCLUSIONS AND FUTURE WORK |
| This paper presents two algorithms for the solution of Multi-objective software module clustering which is more flexible and adoptive in nature even if the number of objectives increases. Additionally, it makes the clusters in maximum possible minimal search. In Genetic algorithm based clustering, finding the fitness value with the consideration of satisfying multiple objectives in efficient way is a challenging task. In future, I intend to continue this to reduce the difference between maximum and minimum number of modules in clusters using effective algorithm. |
References |
|