ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Fayrouz Dkhichi1, Benyounes Oukarfi1
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
This present paper deals with the parameter determination of solar cell by using an artificial neural network trained at every time, separately, by one algorithm among the optimization algorithms of gradient descent (Levenberg-Marquardt, Gauss-Newton, Quasi-Newton, steepest descent and conjugate gradient). This determination issue is made for different values of temperature and irradiance. The training process is insured by the minimization of the error generated at the network output. Therefore, from the outcomes obtained by each gradient descent algorithm, we conducted a comparative study between the overall of training algorithms in order to know which one had the best performances. As a result the Levenberg-Marquardt algorithm presents the best potential compared to the other investigated optimization algorithms of gradient descent
Keywords |
| Artificial neural network, training, gradient descent optimization algorithms, comparison, electrical parameters, solar cell. |
I. INTRODUCTION |
| The exhibitions under irradiance, temperature lead to the degradation of the internal characteristics of solar cell and prevent the photovoltaic (PV) panel to generate electrical power under its optimal performances. In order to study the influence of these handicapping factors, we must know the internal behavior of solar cell by determining the electrical parameters according to different values of irradiance and temperature. |
| The PV current (IPV) produced at the output of solar cell is in a nonlinear implicit relationship with the internal electrical parameters. The latter can be identified analytically [1] or numerically [2] for a specific temperature and irradiance. In other hand, the study of the behavior of solar cell requires the identification of its parameters for various values of irradiance and temperature. Therefore, the Artificial Neural Network (ANN) seems the best adapted to insure this role. |
| The choice behind the use of the ANN returns to its capacity to predict results from the exploitation of the acquired data. The information is carried by weights representing the values of the connections between neurons. The functioning of the ANN requires its training by an algorithm insuring the minimization of the error generated at the output. |
| In the aim to determine the electrical parameters values, we compare in this study between the optimization algorithms of gradient descent that allow the training of the ANN. We distinguish three algorithms of second order of gradient (Levenberg-Marquardt, Gauss-Newton and Quasi-Newton) and two algorithms of the first order of gradient (steepest descent and conjugate gradient). |
| 2.1. Single diode solar cell model |
| In our study the solar cell is modeled by an electrical model [3] with a single diode shown in Fig. 1: |
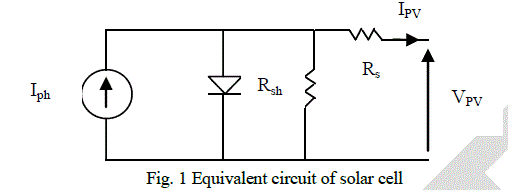 |
| Rs: Series resistance representing the losses due to the various contacts and the connections. |
| Rsh: Shunt resistance characterizing the leak currents of the diode junction. |
| Iph: Photocurrent depending on both irradiance and temperature. |
| Is: Diode saturation current. n: Diode ideality factor. |
| Vth: Thermal voltage (V A.T q). th ïÃâ¬Ã½ T: Temperature of solar cell by Kelvin. |
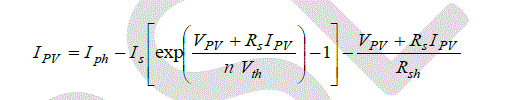 |
| 2.2. The operating process of solar cell under illumination |
| An illuminated solar cell generates a characteristic IPV=f(VPV) for every value of irradiance and temperature. We obtain this characteristic by varying the value of load R (Fig. 2). |
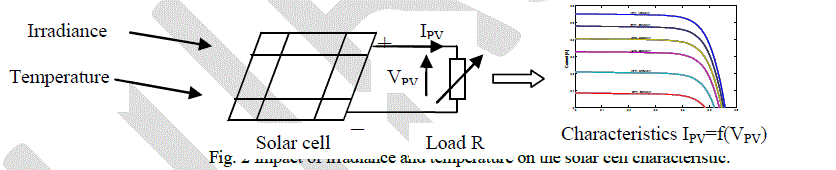 |
| The change of the solar irradiance between 100W/m² and 1000W/m² and the cellular temperature between 18°C and 65°C affects the values of the five electrical parameters Rs, Rsh, Iph, Is, and n of solar cell. Effectively, the current Iph varies according to irradiance and the current Is varies according to temperature while Rs, Rsh and n vary according to the both meteorological factors [4]. |
III. THE USED ARTIFICIAL NEURAL NETWORK |
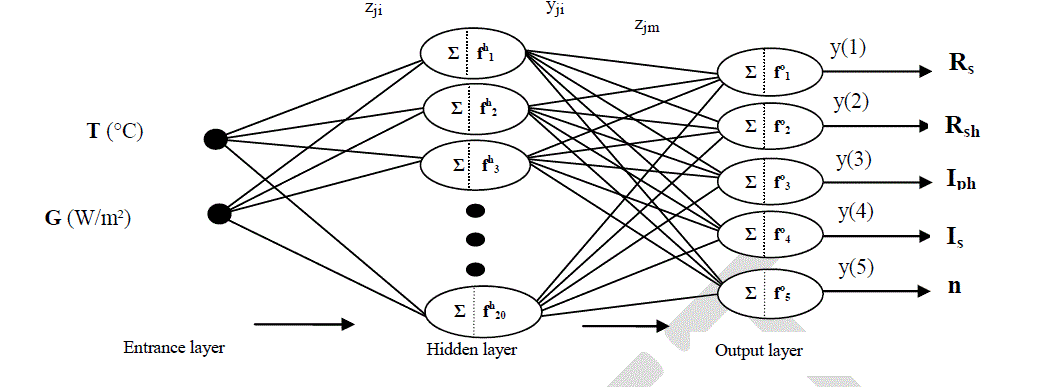
| The identification of the internal electrical parameters for various values of temperature (T) and irradiance (G) is insured by the network ANN [4] shown in Fig. 3. The architecture includes an entrance layer, a hidden layer and an output layer. |
| The entrance layer contains two inputs [T, G], the hidden layer contains twenty hidden neurons and the layer of the output includes five output neurons corresponding to the five parameters Rs, Rsh, Iph, Is and n whose we want to predict the values. |
 |
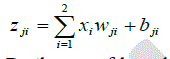 |
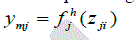 |
V. RESULTS AND DISCUSSION |
| The training of the network is made with 130 inputs-outputs examples distributed in three sets (learning, validation and test) [10]. |
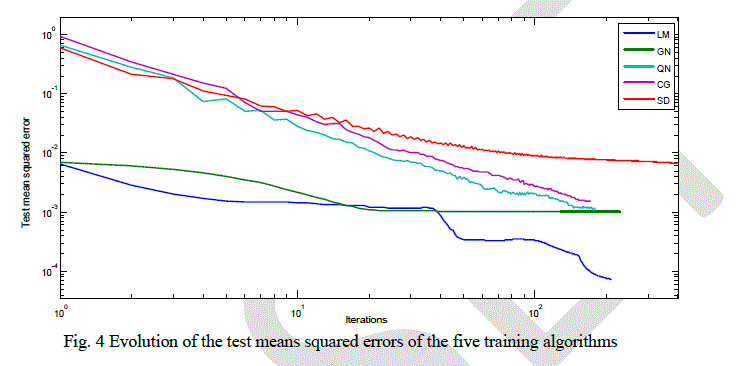 |
| The Fig. 4 shows the curves of the test means squared errors obtained by the ANN. Each curve corresponds one of the five optimization algorithms. We used the logarithmic scale in the axis of iterations in order to well show the behavior of the algorithms convergence. Therefore, the LM algorithm allows a good training of the ANN compared to other algorithms (GN, QN, CG and SD). The both QN and CG have a stiff slope compared to SD which converges slowly (Fig. 4). |
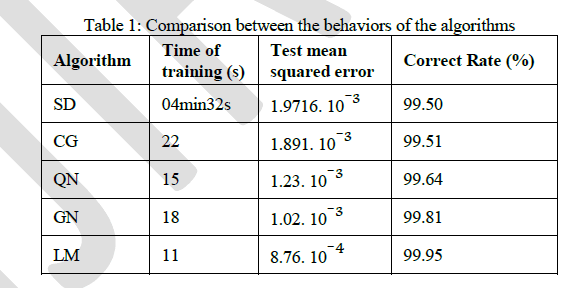 |
| The Table 1 includes the results obtained after training the ANN at every time by one algorithm of the five optimization algorithms. As a result, the SD converges slowly and determines the values of the five electrical parameters at the output of the ANN far from their targets with an error rate of 5%. By comparing the results of this algorithm to those of CG, the latter present fast convergence, but with error rate of 4 %. Both algorithms QN and GN present more important rates of correction: 99.51% and of 99.81% successively. Therefore by comparing the results of LM with that of the SD, CG, QN and GN algorithms, The LM presents better rate of convergence (time of training) and better rate of correction. |
 |
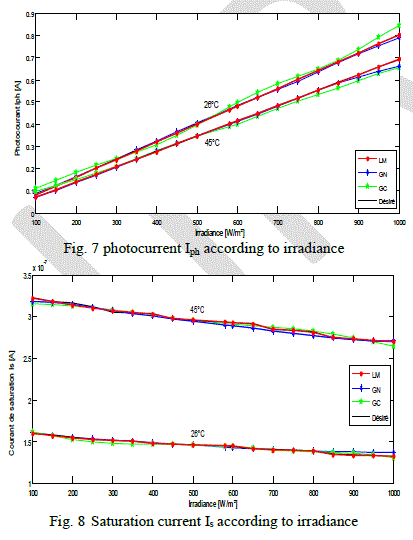 |
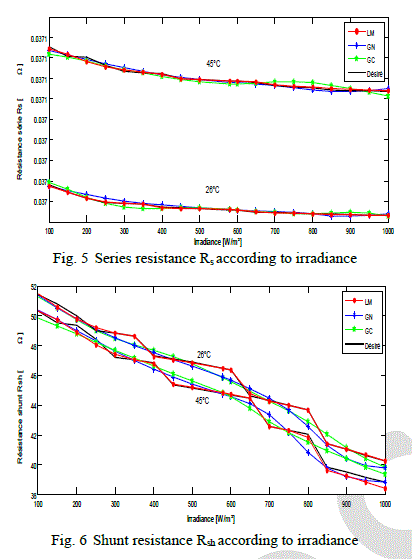
| Figs. 5-9 show the evolution of the parameters Rs, Rsh, Iph, Is and n according to irradiance for two fixed values of temperature (26°C and 45°C) and Figs. 10-14 describe the evolution of the five electrical parameters according to temperature for two fixed values of the irradiance (200W/m² and 400W/m²). We observe that LM gives curves more compatible with those desired. By comparing LM with GN, the latter gives more or less curves close to the desired ones. In other hand, GC generates an error, more important than that observed with GN. |
| The rate correction of SD is low compared to other algorithms and that is explained by its oscillation around the optimum, which prevents the convergence to reach the optimum solution (Fig. 4 and Table 1). The use of the coefficient ïÃÂâïÃâ¬Ã by the Eq. (15), allow to the CG algorithm to converge quickly (Table 1) compared to SD. The QN and GN algorithms present two correction rates more interesting than those of the SD and CG algorithms. This behavior is explained by the fact that QN and GN are better known by their fast convergence near to the optimum. The LM algorithm presents the best behavior of the convergence compared to other algorithms, due to the combination between the features of SD and GN. Therefore, LM behaves as SD for big values of λ And then, it behaves as GN for small values of λ [6] |
VI. CONCLUSION |
| The Levenberg-Marquardt algorithm provides interesting performances at the training of the artificial neural network compared with other optimization algorithms of gradient descent. Effectively, it determines the values of the five electrical parameters of the solar cell so close to desired ones due to its capacity to optimize the mean squared error to the minimal value in a small amount of time. |