Research and Reviews - International Journals

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

New Methods for Finding the nth Root of a Number

Nitin A Jain1, Kushal D Murthy1, Dr. Hamsapriye2
  1. Student, Department of Electronics & Communication Engineering, R.V. College of Engineering, Bangalore, Karnataka, India
  2. Professor, Department of Mathematics, R.V. College of Engineering, Bangalore, Karnataka, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

New methods for finding the nth root of a positive number m, to any degree of accuracy, are discussed. These methods are based on finding eigen values and eigen vectors of a special matrix. For even order matrices, the method is founded on the well-known power method. The desired root and its higher powers can also be obtained from the same matrix.

Keywords
Iterative algorithm, Diagonalization, Power method, Dominant Eigen Value.

AMS Classification
65D99

I. INTRODUCTION
image
Therefore, the successive generation of the sequence of approximations to ��, involve the multiplication of higher powers of the square matrix in (3). The convergence of the iterative algorithm directly depends on the nature of the eigen values and eigen vectors of the matrix.
Based on linear algebra concepts, [3] generealizes and mathematically proves the matrix method of [2]. This generalized form of the square matrix in (3) is given to be
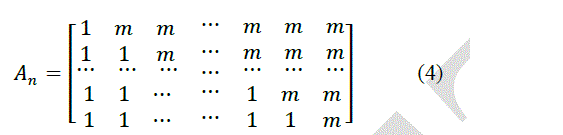image
image
image

References
  1. Kendall E. Atkinson, “An Introduction to Numerical Analysis”, John Wiley & Sons, Second Edition 1988.
  2. Theodore Eisenberg, “On an unknown algorithm for computing square roots”, International Journal for Mathathematical Education in Science and Technology, 34 (1), pp. 153 - 158, 2003.
  3. Nitin A Jain, Kushal D Murthy and Hamsapriye, “Matrix methods for finding n mu”, International Journal for Mathathematical Education in Science and Technology, 45(2), pp. 1 - 9, 2014.
  4. Nitin A Jain, Kushal D Murthy and Hamsapriye, “On Finding the n mu leading to Newton-Raphson's Improved method”, Accepted for publication in International Journal of Emerging Technologies in Computational and Applied Sciences, Issue 9, June - August, 2014.