Research and Reviews - International Journals

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

NUMERICAL SOLUTION FOR BOUNDARY VALUE PROBLEM USING FINITE DIFFERENCE METHOD

R.LAKSHMI1, M.MUTHUSELVI2
  1. Assistant Professor, Department of Mathematics, PSGR Krishnammal College for women, Coimbatore ,Tamil Nadu, India
  2. Assistant Professor, Department of Mathematics, Dr.SNS Rajalakshmi College of Arts and Science, Coimbatore, Tamil Nadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

In this paper, Numerical Methods for solving ordinary differential equations, beginning with basic techniques of finite difference methods for linear boundary value problem is investigated. Numerical solution is found for the boundary value problem using finite difference method and the results are compared with analytical solution. MATLAB coding is developed for the finite difference method. The results are reported for conclusion.

Keywords
Ordinary Differential Equations, finite Difference method, Boundary value problem, Analytical solution, Numerical solution

INTRODUCTION
In mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives. Finite differences method is used in soil physics problems. An important application of finite differences is in numerical analysis, especially in numerical differential equations, which aim at the numerical solution of ordinary and partial differential equations respectively. The idea is to replace the derivatives appearing in the differential equation by finite differences that approximate them. The resulting methods are called finite difference methods. Common applications of the finite difference method are in computational science and engineering disciplines, such as thermal engineering, fluid mechanics, etc.
A. STEPS INVOLVED IN FINITE DIFFERENCE METHOD
A finite difference method typically involves the following steps: Generate a grid, for example (xt ; t (k)), where we want to find an approximate solution.
Substitute the derivatives in a system of ordinary differential equations with finite difference schemes.
The ordinary differential equation then becomes a linear/non-linear system of algebraic equations.
Solve the system of algebraic equations. Implement and debug the computer code.
Do the error analysis, both analytically and numerically.
B. DERIVATION OF FINITE DIFFERENCE METHOD
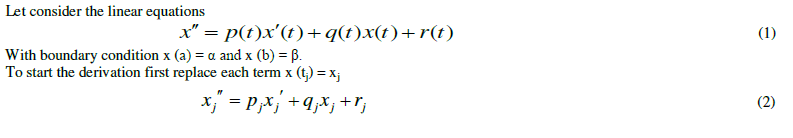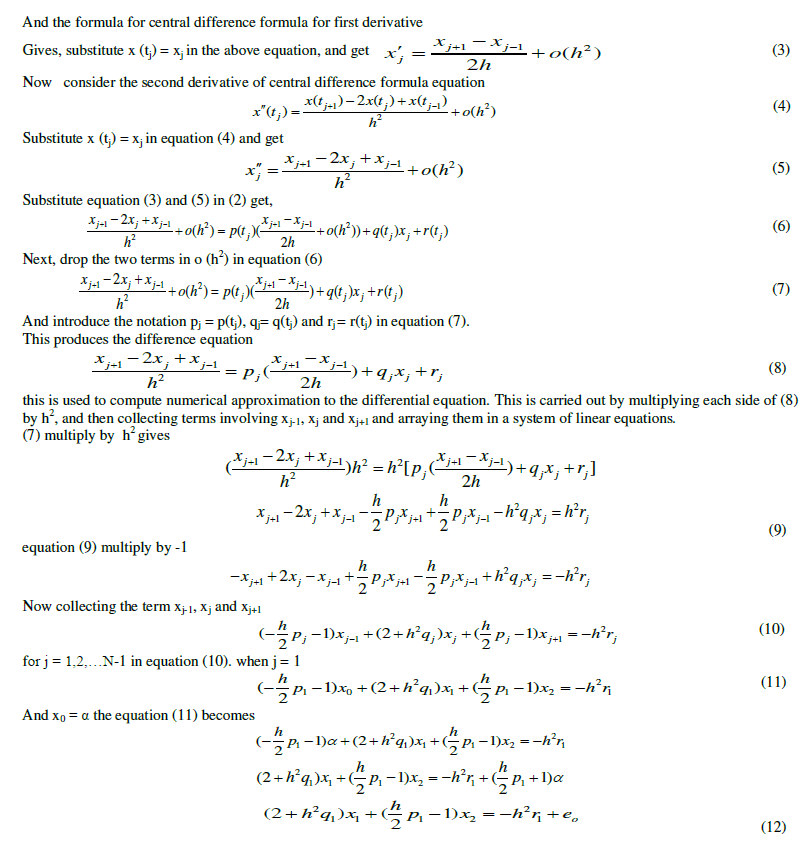image
image
image
image
image
image
image
image
image
image

CONCLUSION
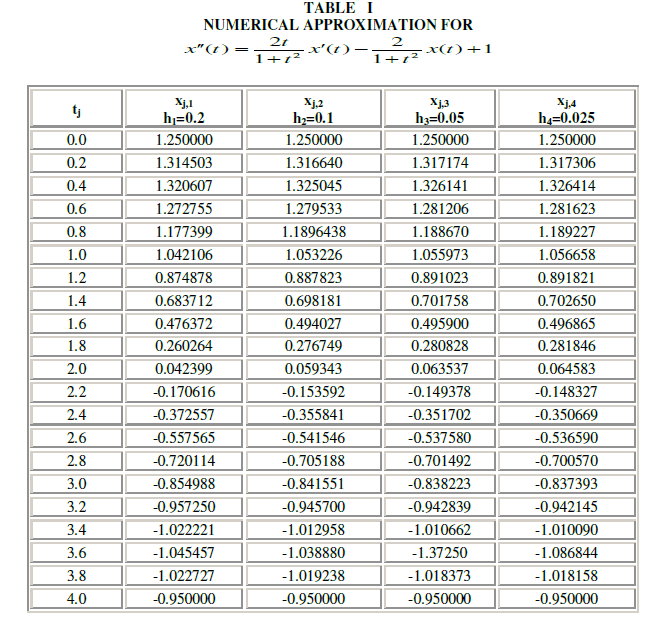
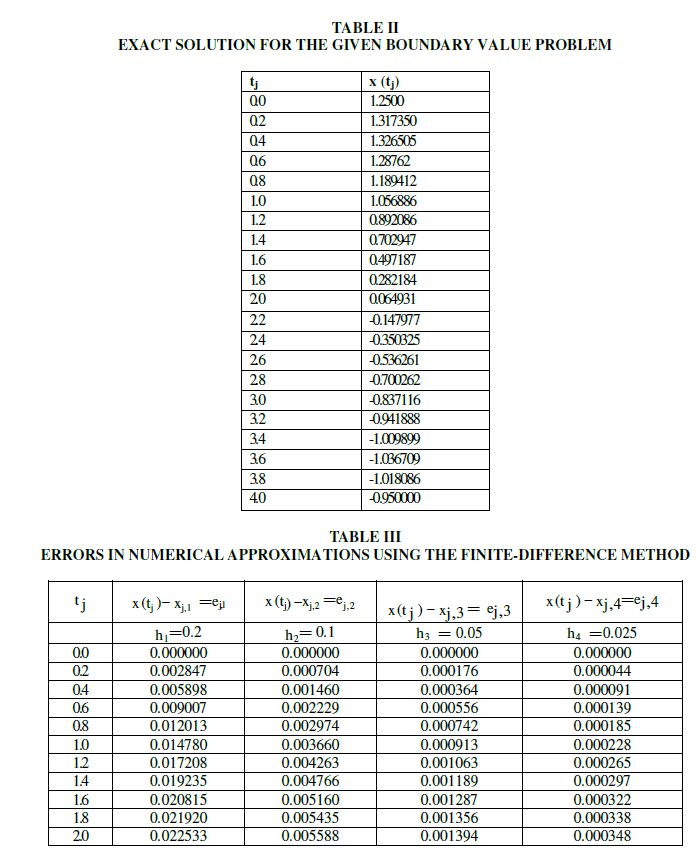
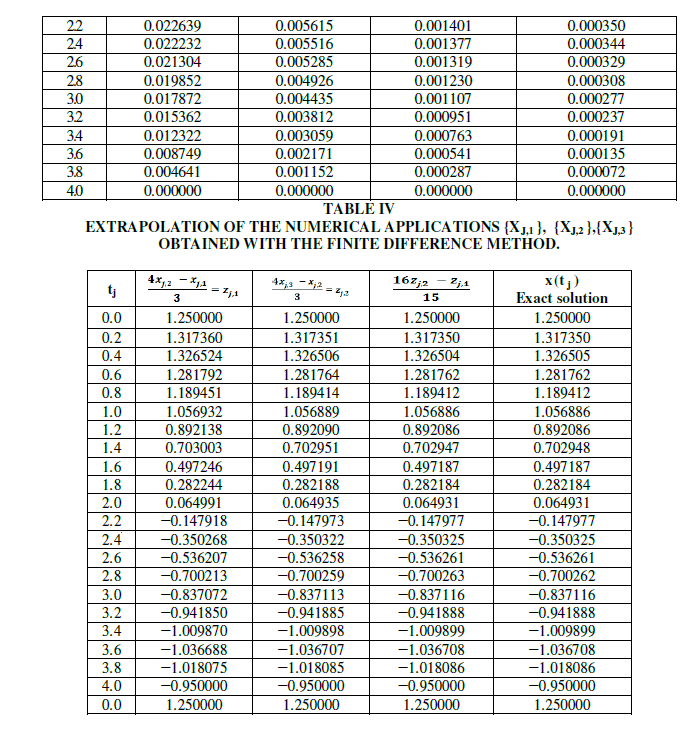
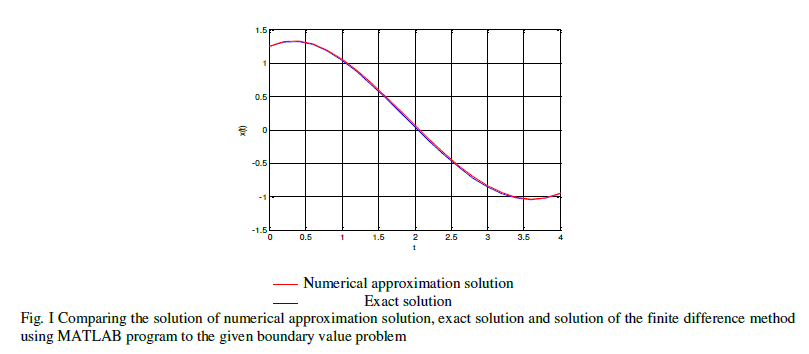
A boundary value problem is solved using finite difference method and is verified with exact solution. It is found that the results are agreed with exact solution.

References
  1. John H.Mathews , Kurtis D. Fink, Numerical Methods Using MATLAB, Fourth Edition,2008, Published by Dorling Kindersley(INDIA)Pvt.Ltd., New Delhi.
  2. DR. M. K. Venkataraman, Numerical Methods in Science And Engineering, Fifth Edition (Revised & Enlarged ), 2004, The National Publishing co., Chennai.
  3. H. C. Saxena, Finite-Differences and Numerical Analysis, Thirteen Revised Edition, 1997, Published by S. Chand& Company Ltd., New Delhi.
  4. Laurence V. Fausett, Applied Numerical Analysis Using MATLAB, Second Edition, 2009, Published by Dorling Kindersley(INDIA)Pvt.Ltd., Noida.
  5. http://www.mathwork.com/matlab/fd/method.