ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Osama H. M.1, Fadhel S. F.1 , Zaid A. M.2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
This paper presents a clear procedure for the fractional variational solution via Haar wavelet technique. The fractional derivative is defined in the Riemann-Liouville sense. The fractional variational problem is solved by means of the direct method using the Haar wavelet and the problem will be reduced to the solution of an algebraic equations. The numerical solution for the class of problem considered can be obtained directly from the functional and there is no need to solve the fractional Euler-Lagrange equation. The examples are included in order to demonstrate the validity and applicability of the suggested approach.
Keywords |
| Haar wavelet method, Fractional calculus, Calculus of variation, Fractional calculus of variation. |
INTRODUCTION |
| The use of fractional calculus of modeling physical system has been widely considered in the last decades, [1]. Although, the concept of the fractional derivatives was introduced already in the middle of the 19th century by Riemann and Liouville, [2]. The first work, devoted exclusively to the subject of fractional calculus, is the book by Oldham and Spanier [3] published in 1974. After that, the number of publications about the fractional calculus has rapidly increased. The reason for this is that the same physical processes as a anomalous diffusion, complex viscoelastisity, behaviour of mehatronic and biological systems, rheology, etc. can be described adequately by classical models, [2]. A fractional calculus of variations problem is a subtopic of fractional calculus and it is a problem in which either the objective functional or the constraint equation or both contain at least one fractional derivative term, [4]. This occurs naturally in many problems of physics, mechanics and engineering in order to provide more accurate models of physical phenomena (see [5-13]), However, the fractional calculus of variations is a new field, ;Its starting point appear to be the references [14], [15] where Riewe developed the nonconcentrative Lagrangian, Hamiltonian, and other concepts of classical mechanics using fractional derivative, [16]. Particularly, a fractional calculus of variation concerns the variational principles on functionals involving fractional derivative as we mention above and this leads to the statement of fractional Euler-Lagrange equations (see [14], [4], [17]). Fractional Euler-Lagrange equations are difficult to solve explicitly and consequently it is of interest to develop efficient numerical schemes for such dynamical systems. In this paper, we shall use the direct Haar wavelet method for a class of fractional variational problems. Haar wavelet theory has been innovated and applied to various fields in engineering ([18]-[25]), and have proved to be a wonderful mathematical tool. |
| The idea of this paper is to introduce Haar wavelets, then present a direct method for solving fractional problems via Haar wavelets. The procedure begins by assuming the admissible functions by Haar wavelets with coefficients to be determined, then establishing an operational matrix for performing integration and finding the necessary condition for exterimization, solving the resulting algebraic equation yields the Haar coefficients. This indicates that for the class of problems that will be considered, the numerical solution can be obtained directly from the functional, and there is no need to solve the fractional Euler-Lagrange equations. |
FRACTIONAL DERIVATIVE AND INTEGRATION |
| In this section, we shall review the basic definitions and properties of fractional integral and derivative, which are used further in this paper, [1]. |
| Definition (1): |
| The Riemann-Liouville fractional integral operator of order α > 0, is defined as: |
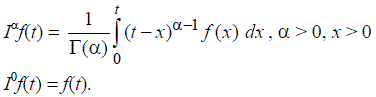 |
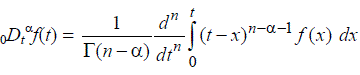 |
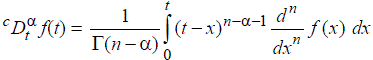 |
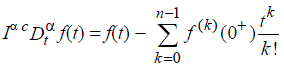 |
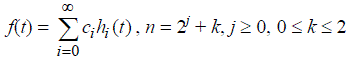 |
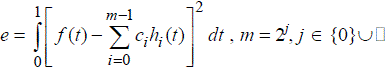 |
 |
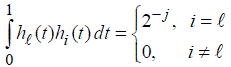 |
 |
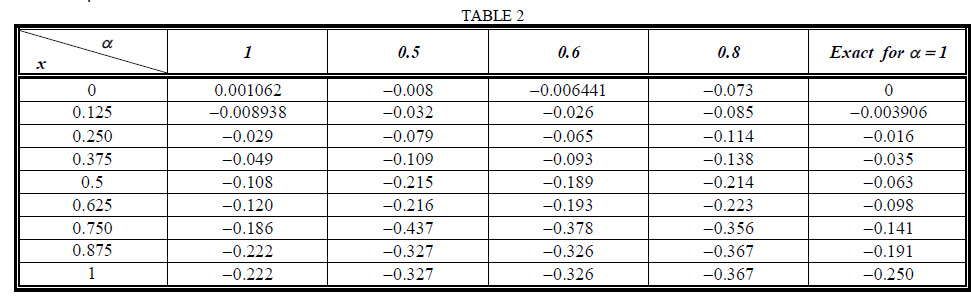 |
CONCLUSION AND DISCUSSION |
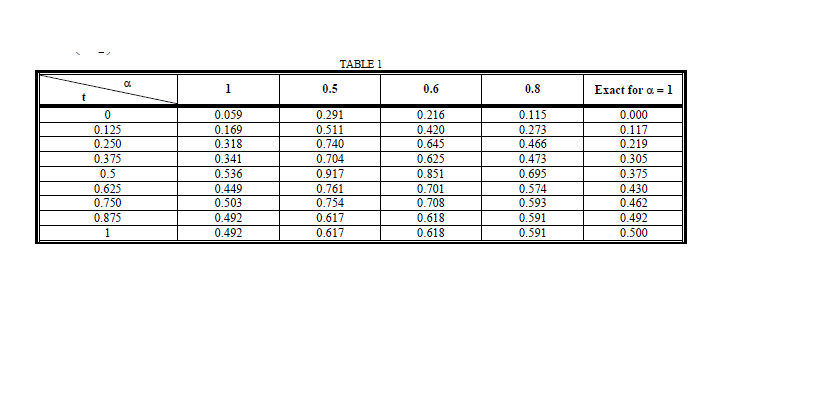
| Direct Haar wavelet method has been presented for a fractional variational problem. The procedure considered in this paper can be considered as a generalization to the results given in [28]. From the illustrative examples, it ca be seen that this operational matrix approach can obtain accurate and satisfying results. All computational results are made by MATLAB program. |
References |
|