Numerical Study of Transient Forced
Convection Heat Transfer in Square Duct with
Nanofluid

Ahmed. H. Ali; Tahseen.A.Al-Hattab

Numerical Study of Transient Forced Convection Heat Transfer in Square Duct with Nanofluid

Ahmed. H. Ali¹ and Tahseen.A.Al-Hattab ²

Department of Automotive, Technical College of Najaf, Najaf, Iraq
Department of Electrochemical Engineering, University of Babylon, Babylon, Iraq

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

In the present paper, the problem of transient laminar forced convection flow of nanofluids in horizontal square duct has been thoroughly investigated using a single phase approach. The water is adopted as base fluid ,while the(Al2O3) and(CuO) are a solid nanoparticles. Computations are validated with experimental data available in the literature, good agreements are obtained. The results showed that Convective heat transfer coefficient for nanofluids is greater than that of the base liquid. Heat transfer enhancement increases with the particle volume concentration increase, but it is accompanied by increasing wall shear stress values. The isotherms are presented for various void fractions and Reynolds numbers. Also, the relation between the Nusselt number, and friction factor with Time are introduced for various Reynolds numbers and volume fraction of nanoparticles.

KEY WORDS

TRANSIENT FORCED CONVECTION, SQUARE DUCT, LAMINAR FLOW, NANOFLUID, CONSTANT HEAT FLUX

I. INTRODUCTION

The augment of heat transfer rate is one of the most important technical aims for industry and researches. Also, the decrease in the pressure drop for systems that generate high fluid pressure drop is very noticeable. The heat convection can passively be enhanced by changing flow geometry, boundary conditions or by enhancing fluid thermophysical properties. Nanofluids are liquids that containing nanopowders with dimensions smaller than 100 nm and are suspended in base fluid such as water, oil or ethylene glycol.

II. RELATED WORKS

Nanofluids are best for applications in which fluid flows through small passages because nanoparticles are small enough to behave similarly to liquid molecules. Xuan and Roetzel[1] were showed that the thermal conductivity of the suspensions can increase by more than 20% causing increase in heat transfer rate. MaÃÂ±¨ga et al.[2] developed numerical simulation for the hydrodynamic and thermal characteristics of a laminar forced convection flow. Results showed that heat transfer enhancement that appears to be more pronounced with the increase of the particle volume concentration is accompanied. Later, Akbarinia and Behzadmehr[3] Fully developed laminar mixed convection of a nanofluid numerically. they estimated water and Al2O3 in 3-D horizontal curved tubes. They concluded that The nanoparticles volume fraction does not have a direct effect on the secondary flow, axial velocity and the skin friction coefficient. Akbari et al.[4] offered Numerical investigation of fully developed laminar mixed convection with single phase model used(water+ Al2O3). The results illustrate that the nanoparticles concentration does not have significant effect on the secondary flow, axial velocity profile and also on the peripherally average skin friction coefficient. Izadi et al.[5] studied Heat transfer mechanisms in annulus with Laminar forced convection of a nanofluid numerically. They found that the dimensionless axial velocity profile does not significantly change with the nanoparticle volume fraction. But, the temperature profiles are affected by the nanoparticle concentration. He et al.[6] performed Numerical simulations using a single and combined Eulerian and Lagrangian method on the convective heat transfer of aqueous γ-Al2O3 nanofluids flowing through a straight tube under the laminar flow conditions. Lotfi et al[7] submitted Forced convective of a nanofluid that consists of water and Al2O3 in horizontal tubes. Authors reported that "It is clear from the results that the rate of thermal enhancement decreases with the increase of nanoparticles volume concentration". Mansour et al.[8] were studied mixed convection flows in a square lid-driven cavity partially heated. various volume fractions of (Cu, Ag, Al2O3 and TiO2) and results refer to adding alumina will provide highest Nusselt number. And in the same time, using TiO2 will reduce heat transfer enhancement to lest. Farhad Talebi [9] were designed model to simulate numerically a laminar mixed convection flows through a copper–water nanofluid in a square lid-driven cavity. They seem that solid concentration has a positive effect on heat transfer enhancement.

Experimental studies on convective heat transfer of Cu/Water,CuO/Water and Al2O3/Water nanofluids are reported by Zeinali et al.[10,11]. The experimental set-up consisted of a one-meter annular tube, which was constructed of 6 mm diameter inner cupper tube 0.5 mm thick, and 32 mm diameter outer stainless steel tube. The nanofluid flows inside the inner tube while saturated steam entered the annular section, which created constant wall temperature condition.

Also, Nassan et al. [12], presented a single-phase model to study the laminar flow and heat transfer characteristics of nanofluids in a square duct experimentally in steady state condition. indicate that a considerable heat transfer enhancement has been achieved by both nanofluids compared with base fluid. However, CuO/water nanofluid shows better heat transfer intensification compared with Al2O3/water nanofluid through square cross-section duct. Sundar and Sharma[13] were studied The single phase turbulent convective heat transfer of Al2O3 nanofluid in a circular tube with different aspect ratios of longitudinal strip inserts. an effective increasing (reaches to 30.3%) when compared to water at 0.5% concentration and maximum Reynolds number used.

The main endeavor of this study is numerically investigation of the transient behavior of laminar flow forced convection with various concentrations of nanoparticles and given Reynolds number on the heat transfer enhancement.

PROBLEM CONFIGRATION AND BOUNDARY CONDITIONS

Fig.(1)shows the geometrical configuration under consideration. It consists of a tube with a length (L) in the Xdirection, while The height and width of duct is (H).The nanofluid considered is composed of water and Al2O3 or CuO particles. The fluid enters with uniform temperature and axial velocity profiles at the inlet section. The duct has appropriate length in order to obtain fully developed profiles(velocity and thermal) at the outlet section.

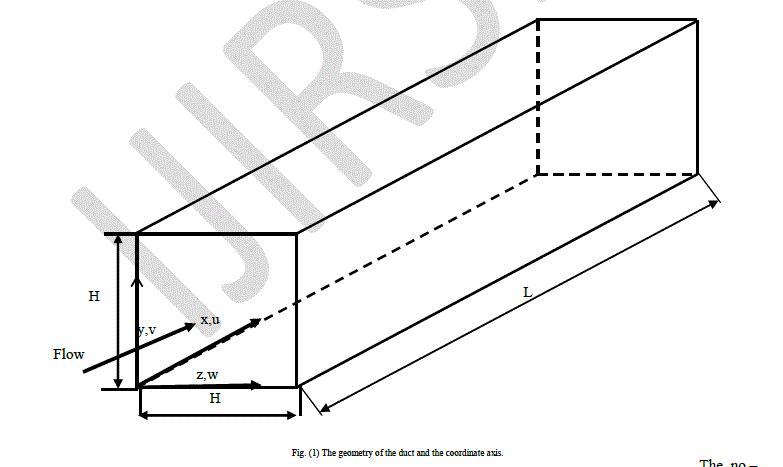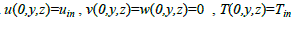III. MATHEMATICAL MODELING

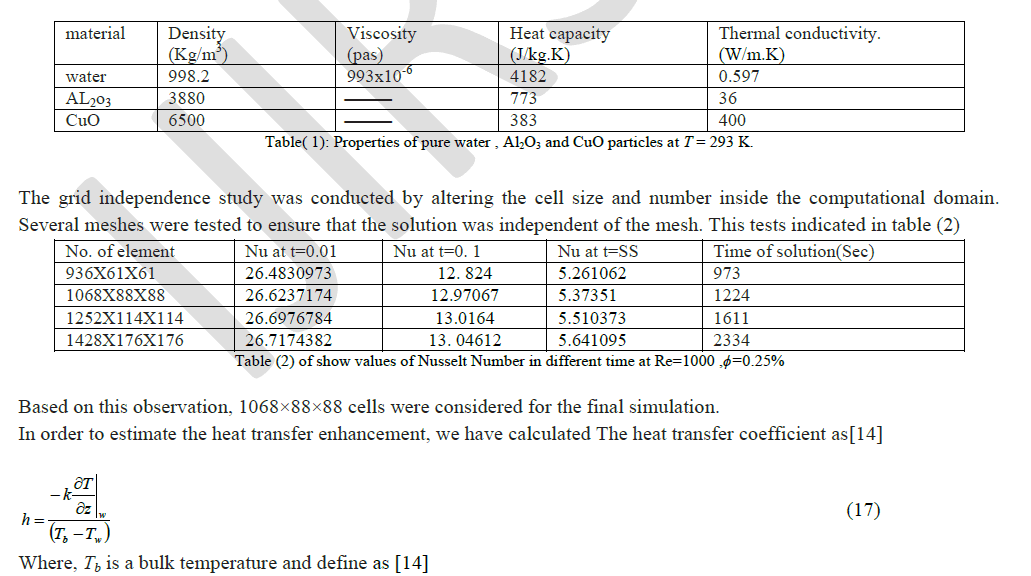
The flow is assumed to be Newtonian, three-dimensional and incompressible. It is also assumed that the base fluid and the nanoparticles are in thermodynamic equilibrium and that they flow at the same velocity. The viscous dissipation terms and thermal radiation are assumed to be negligible. The governing equations for 3-D transient laminar with forced convection of constant properties are modeled as

Continuity Equation

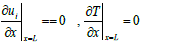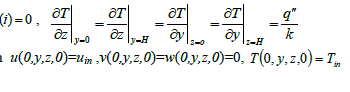IV. COMPUTATIONAL PROCEDURE

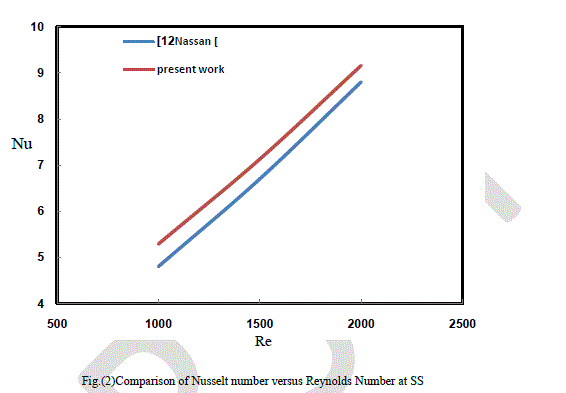
The governing equations with boundary and initial conditions are solved numerically by using commercial software COMSOL 3.5 which depends on finite element technique. The validation of the computational results is achieved by comparison with that of Nassan et al.[12] for experimental nanofluids in square cross-section duct as shown in figure (2). The Thermo physical properties of water, Alumina and Copper oxide are listed in table (1).

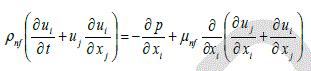V. RESULTS AND DISCUSSION

After determination the properties of nanofluid, discretization the domain and coupled governing equations, and assigning the initial, final and step for dimensionless times as 0.001, 0.01, 0.1 and at Steady State respectively.

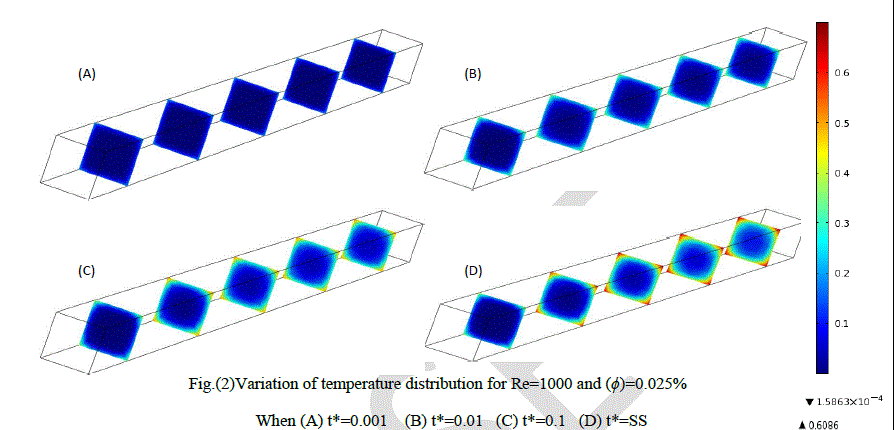Figures (2 through 4) show the temperatures behavior with time for different values of (ÃÂ) , axial distance at time period. The increase of temperature with increasing of time can be showed obviously. there are some hottest regions inside duct especially at corners where that refer to low velocity compared with others regions, since the fluid takes enough time to transfer the heat from each other and from the wall. And as time travelled, temperature of bulk fluid increase gradually and this raising keep on until reaching steady state condition. it is observed that the regions of isotherms are mostly symmetric with respect to the center of the duct. Moreover, above figures provide a proof that increasing (ÃÂ) only with fixing the rest of the parameters causes reduction in bulk temperature. The high thermal conductivity and Reynolds number is the main reason to accelerate transient state as the volume fraction increases.

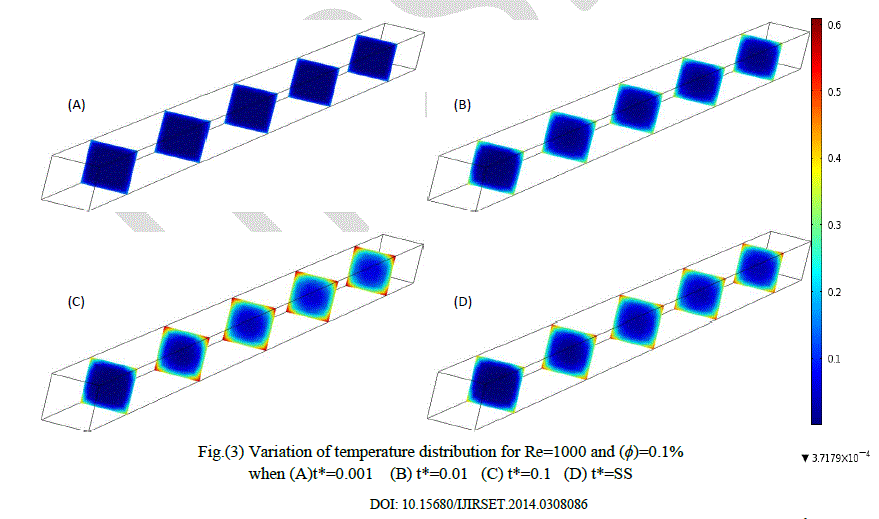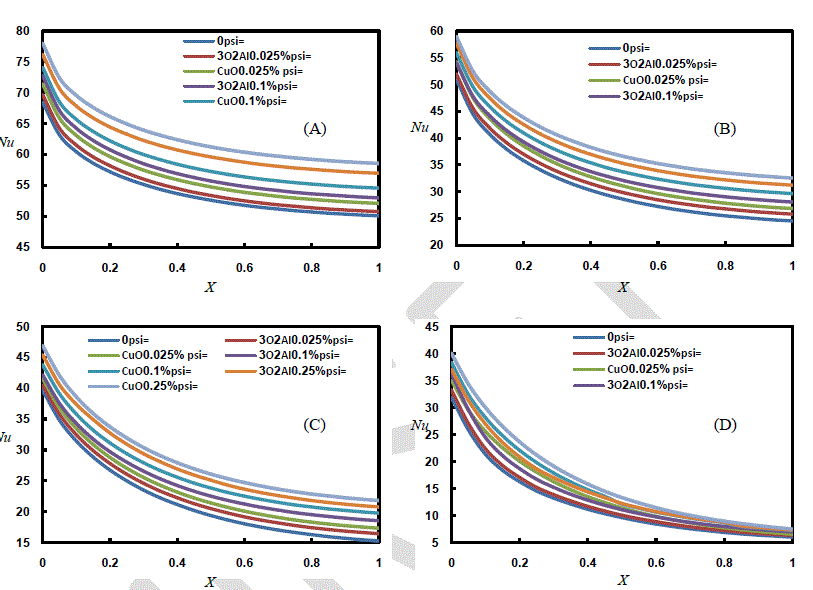
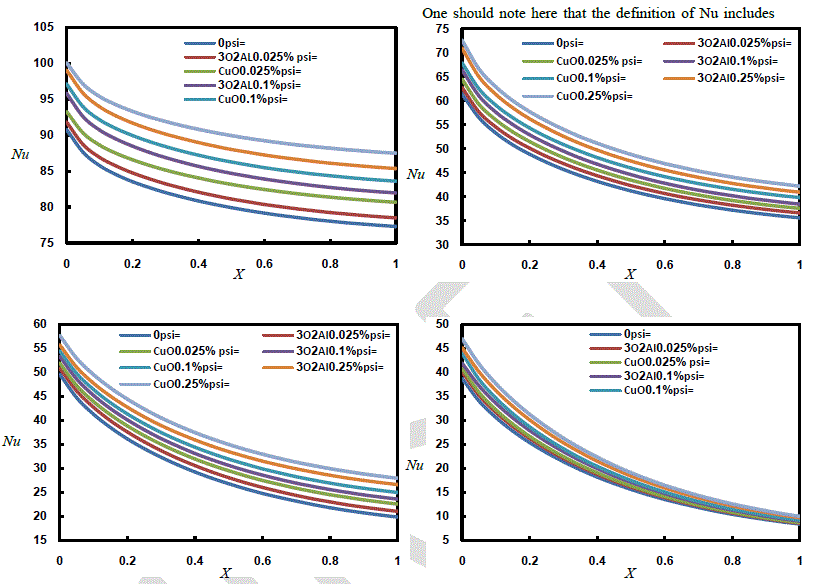
Local Nusselt Number variation with duct length at a different values of Reynolds Number, time and given volume construction are demonstrates in Figs.(5-6).it is clear that increasing of volume construction cause an active increase in Nusselt Number at specified Re. the phenomena of increasing Nusselt Number referred to increase of thermal conductivity of nanofluid compared of bulk fluid. At the beginning of flow, there are immense difference in temperature variation between wall and bulk nanofluid led to maximum value of Nu. Another reason that little boundary layer thickness at the inlet of the entry region, causing high Local Nu, and as the thickness of the thermal B.L. increases, the local Nu decreases and then, reaches to small variation in its value as the thermal B.L. head to the center of the channel.

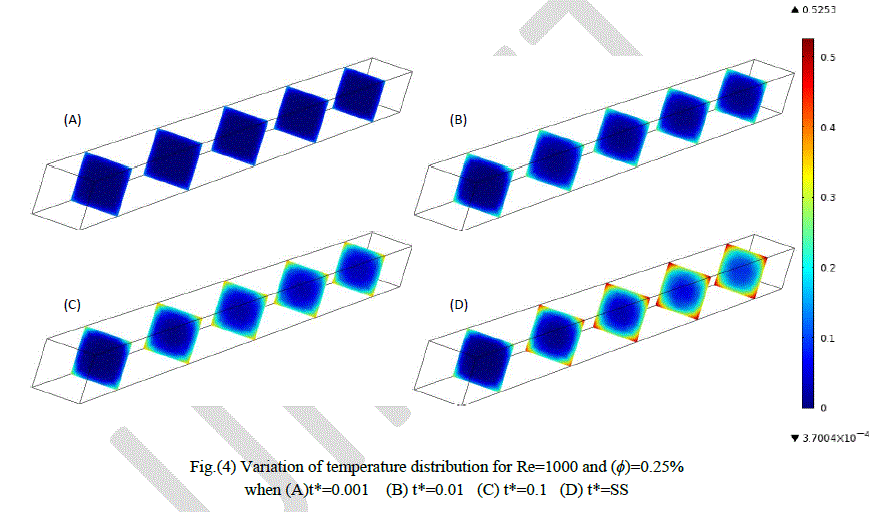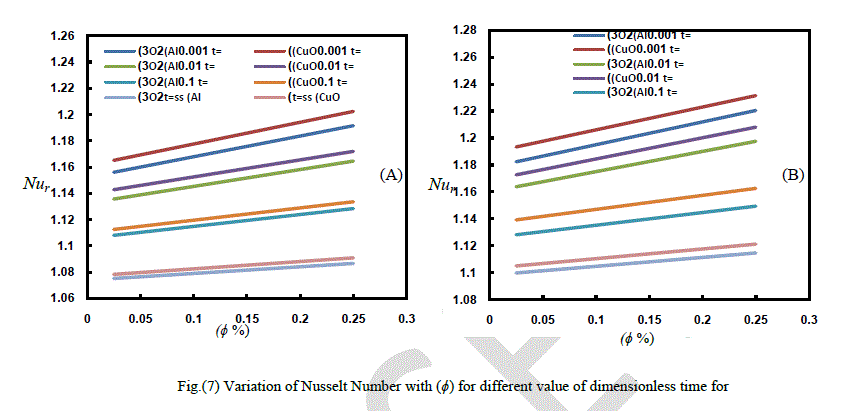
Fig. (7) show the average variation of Nusselt Number versus time as a function of loaded particles, for all implemented Reynolds numbers. It can be seen that the heat transfe rate increases with nanoparticles concentration. Also, a comparison between (A) and (B) in Figure(7) shows that Nu of CuO nanofluid is larger than of Al2O3 nanofluid, at specified Re and (ÃÂ)

in the same time, according to mentioned figures, average Nusselt ratio decrease with time passing because in the beginning of flow, the presence of the nanoparticles changes and enhances the temperature distribution making it more uniform which means more energy transfers through the fluid comparison with the same time period of that of base fluid.

VII. CONCLUSION

The model was applied to simulate the transient forced convection flows of Alumina–water and Copper oxide-warer nanofluid in a horizontal square duct for different Reynolds numbers and void fractions of nanoparticles. The results showed at a given Reynolds number, solid concentration has appositive effect on heat transfer enhancement. Also, there is an enhancement in heat transfer features where times for converting to steady state is lower than that of base fluid. In addition, the average Nusselt number is highly dependence on the void fraction. This point is also observed in the computation of the dimensionless temperature.

Nomenclature

A Area

Cp Specific heat at constant pressure

Dh Hydraulic diameter

h Heat transfer coefficient

k Thermal conductivity

L Duct length

H Square side length

Nu Nusselt number

p Pressure

P* Dimensionless pressure

Pe Peclet number

Re Reynolds number

Pr Prandtle number

T Temperature

t Time

U, V,W Dimensionless velocity components

u, v,w Velocity components

x, y,z Cartesian coordinates

X, Y,Z Dimensionless coordinates

Greek symbols

α thermal diffusivity

Φsolid volume fraction

μ dynamic viscosity

θ dimensionless temperature

ρ density

τ dimensionless time

Subscripts

bf Bulk fluid

w Wall

in Inlet

nf Nanofluid

p particles

Superscripts

* Properties dimensionless sign

Abbreviations

CHF Constant Heat Flux

SS Steady State

References

Yimin Xuana, and Wilfried Roetzel, “Conceptions for heat transfer correlation of nanofluids”, International Journal of Heat and Mass Transfer, Vol.43, pp.3701-3707, 2000.
Sidi El Be´caye MaÃÂ±¨ga, Samy Joseph Palm, Cong Tam Nguyen, Gilles Roy, and Nicolas Galanis, “Heat transfer enhancement by using nanofluids in forced convection flows”, International Journal of Heat and Fluid Flow, Vol.26, pp.530–546, 2005.
Akbarinia, A., and Behzadmehr, A., “Numerical study of laminar mixed convection of a nanofluid in horizontal curved tubes”, Applied Thermal Engineering Vol.27, pp.1327–1337, 2007.
Akbari, M., Galanis N., and Behzadmehr, A., “Comparative analysis of single and two-phase models for CFD studies of nanofluid heat transfer”, International Journal of Thermal Sciences, Vol.50, pp.1343-1354, 2011.
Izadi, M., Behzadmehr, A., and Jalali-Vahida, D., “Numerical study of developing laminar forced convection of a nanofluid in an Annulus”, International Journal of Thermal Sciences, Vol.48, pp.2119–2129, 2009.
Yurong He, Yubin Mena, Yunhua Zhao, Huilin Lu, and Yulong Ding, “Numerical investigation into the convective heat transfer of TiO2 nanofluids flowing through a straight tube under the laminar flow conditions”, Applied Thermal Engineering, Vol.29, pp. 1965–1972, 2009.
Lotfi, R., Saboohi, Y., and Rashidi, A.M., “Numerical study of forced convective heat transfer of Nanofluids: Comparison of different approaches”, International Communications in Heat and Mass Transfer, Vol.37, pp.74–78, 2010.
Mansour, M.A., Mohamed, R.A., Abd-Elaziz, M.M., and Ahmed, S.E., “Numerical simulation of mixed convection flows in a square lid-driven cavity partially heated from below using nanofluid”, International Communications in Heat and Mass Transfer, Vol.37, pp.1504–1512, 2010.
Farhad Talebi, Amir Houshang Mahmoudi, and Mina Shahi, “Numerical study of mixed convection flows in a square lid-driven cavity utilizing nanofluid”, International Communications in Heat and Mass Transfer, Vol.37, pp.79–90, 2010.
ZeinaliHeris, S., Etemad, SGh., Nasr Esfahany, M. “Experimental investigation of oxide nanofluid laminar flow convective heat transfer in circular tube”, International Communication in Heat and Mass Transfer, Vol.33, pp. 529–533, 2006.
ZeinaliHeris, S., Nasr Esfahany, M., Etemad, SGh., “Experimental investigation of convective heat transfer of Al2O3/Water nanofluid in circular tube”, International Journal of Heat and Fluid Flow, Vol.28, pp.203–210, 2007
Nassan, T.H., Zeinali Heris, S., and Noie, S.H., “A comparison of experimental heat transfer characteristics for Al2O3/water and CuO/water nanofluids in square cross-section duct”, International Communications in Heat and Mass Transfer Vol.37, pp.924-928, 2010.
Syam Sundar, L., and Sharma, K.V., “Heat transfer enhancements of low volume concentration Al2O3 nanofluid and with longitudinal strip inserts in a circular tube”, International Communications in Heat and Mass Transfer Vol.53, pp.4280-4286, 2010.
White, F. M., “Viscous Fluid Flow (3rd Ed.)”, McGraw Hill, New York, 2006.