International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

On A New Model of Human Mortality

Abdushukurov A.A.1, Vassiev E.N.2
  1. Professor, Head of Department of Probability Theory and Mathematical Statistics, National University of Uzbekistan, Tashkent, Uzbekistan
  2. Teacher, Higher Technical School of Fire Safety of the Ministry of Internal Affairs of the Republic of Uzbekistan, Tashkent, Uzbekistan
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

In this paper the main objective is to proposing of new survival function for human mortality data. We study strong consistency and unbiasedeness properties of parameters of survival function.

Keywords
survival function, mortality, consistency.

INTRODUCTION
Statistical methods are playing an increasingly important role in many fields of practical research. Survival analysis is a branch of statistics which deals with death in biological organisms and failure time in mechanical systems. This topic is called reliability theory or reliability analysis in engineering and duration analysis (or duration modeling) in economics or sociology. Survival analysis attempts to answer questions such as: what is the fraction of population which will survive past a certain time? Therefore the object of primary interest is the survival function also called survivorship function, which is defined as
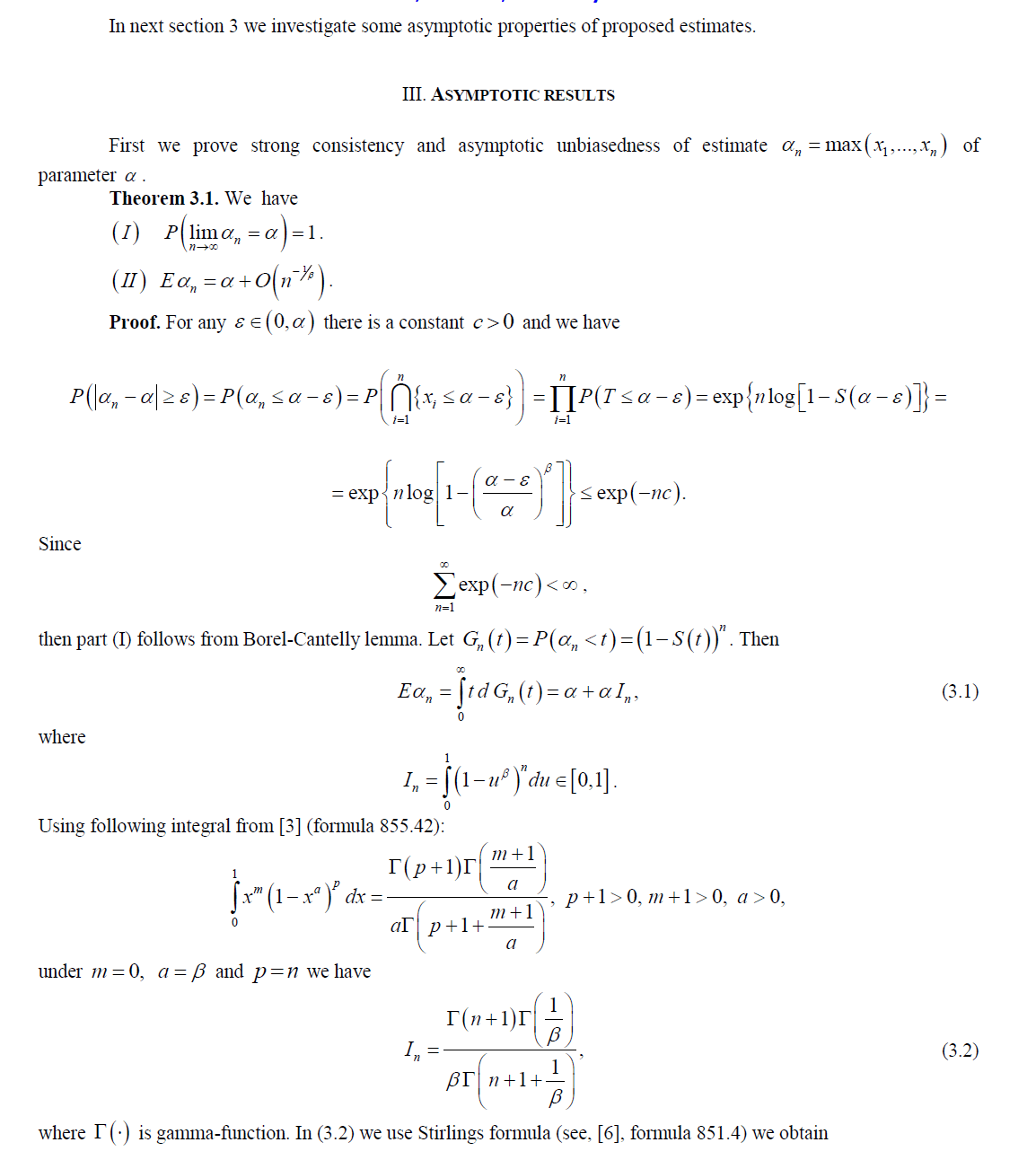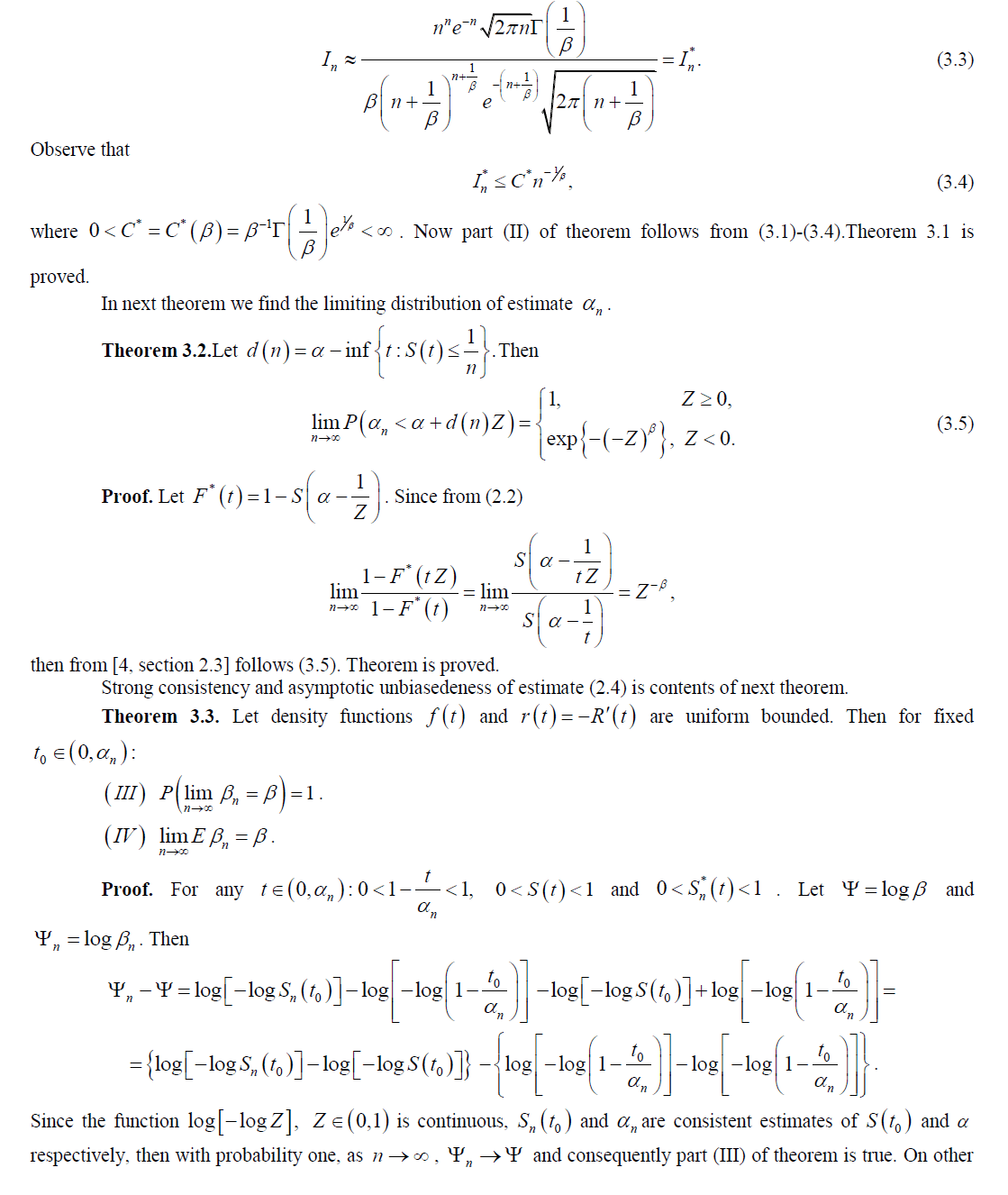image
image
image
image
image
image
Here, the first top corresponds to newborn child’s mortality, second one for teenager’s mortality and thirth one for old man’s mortality with mode mode t mode= 73 years

References
  1. Bowers , N., Gerber, H., Hickman, J., Jones, D., Nesbit, G. “Actuarial Mathematics”, Itasca, IL: The Society of Actuaries, 1986.

  2. Cramer, H. “Mathematical Methods of Statistics”, Stockholm, 575p., 1946.

  3. Dvayt, G.B. “Tables of Integrals”, Nauka, Moscow, 232p., 1969. (In Russian).

  4. Galambos, J. “The asymptotic theory of Extreme Order statistics”, John Wiley & Sons Inc., 1978.

  5. Grandell, J. “Aspects of Risk Theory”, Springer-Verlag, Berlin, 175p., 1991.

  6. Kendall, M.G., Stuart, A. “The Advanced Theory of Distributions”, Vol. I. Distribution Theory, Charles Griffin & Company Limited, London, 1946.

  7. Slud, E.V. “Actuarial Mathematics and Life-Table Statistics”, University of Maryland, College Park, 2001.