ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
P.K. Srivastava1, V.N.Jha2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this present paper we have obtain the fundamental metric function of two dimensional Finsler space whose geodesics are semi-cubical parabolas. We showed that such space is locally Minkowskian.
Keywords |
| Keywords: Finsler space, Two Dimensional, Geodesics, Locally Minkowskian |
INTRODUCTION |
| The fundamental idea of a Finsler space may be traced back to the famous lecture of Riemann’ at Göttingen in 1854. He discussed various possibilities by means of which an n-dimensional manifold may be equipped with a metric and paid special attention to a metric defined by the positive square root of a positive definite quadratic differential form. In this way he laid down the foundation of Riemannian geometry. He also suggested that the positive fourth root of a fourth order differential form might serve as a metric function. This function has three properties in common. It is positive definite, homogeneous of the first degree in the differential and is also convex in the later. Riemann was not hopeful about the geometrical interpretation of the results in such space and therefore he made the following comments: |
| "Investigation of this more general would actually require no essential different principles, but it would be rather time consuming and throw relatively little new light on the study of space especially since the results cannot be expressed geometrically." |
| It is remarkable that the first systematic study of manifolds equipped with such a metric was delayed by more than 60 years. Twenty four years old young German Paul Finsler started the study of Finsler Geometry and submitted his epocmaking thesis to Gottingen University in 1918. He studied this geometry from the stand point of a generalization of the calculus of variation. Finsler derived the idea almost directly from the calculus of variations, with particular reference to the new geometrical background which was introduced by his teacher ‘Cartheodory’ in connection with problems in parametric form. |
| The history of development of Finsler Geometry can be divided into four periods. |
| The first period of the history of Finsler geometry began in 1904, when three geometers J.H. Taylor [21], J.L. Syange [20] and L. Berwald [16] simultaneously started the work in this field. Berwald is the first man who has introduced the concept of connection in the theory of Finsler spaces. He developed a theory with particular reference to the theory of curvature in which the Ricci’s lemma does not hold good. J.H. Taylor and J.L. Synge introduced a special parallelism. In 1928, Taylor gave the name 'Finsler Space' to the manifold equipped with this generalized metric. |
| The second period started in 1934, when E. Cartan [12] published his thesis on Finsler geometry. He showed that it was indeed possible to define connection coefficients and hence covariant derivatives, such that the Ricci’s lemma is satisfied. On this basis Cartan developed the theory of curvature, torsion and discussed geometry of Finsler spaces by his approach. Many mathematician such as E.T. Devies [13], S. Golab [15], H. Hombu [16], O. Varga [22], V.V. Wagner [23] studied Finsler geometry along Cartan’s approach. The above mentioned theories explored certain devices, which basically involves the consideration of a space whose elements were not the points of the underlying manifold, but the line elements, which form a (2n – 1) dimensional variety. |
| The third period of the history of Finsler geometry began in 1951 when H.Rund [18] introduced a new process of parallelism from the stand point of Minkowskian geometry. It was emphasized that the local metric of a Finsler space is a Minkowskian one and that the arbitrary imposition of a Euclidean metric would to some extent, obscure some of the most interesting characteristics of the Finsler space. Latter on E.T. Davies [13] and A. Deicke [14] have indicated that Rund’s and Cartan’s parallelism were the same. Several Mathematicians such as W. Barthel [10] A Deicke [14], D. Laugwitz [17], R.Sulanke [19] have studied Finsler spaces on Rund’s approach. |
| The fourth period started in 1963, when the Finsler geometry came under the influence of Topology. H. Akabar Zadeh [9] developed the modern theory of Finsler spaces based on the theory of connections in fibre bundles. The reason of modernization is to establish a global definition of connections in Finsler spaces and to re-examine the Cartan’s sytem of axioms. The study on this line started when Matsumoto organized symposium on the models of Finsler spaces in 1970. Several mathematicians are working in this field. Some of them are S.S. Chern, D.Bao, Z.Shen, R.L. Bryant, Burogo, etc. The era of applications of Finsler geometry began with the work of R.S. Ingarden [1]. Several Mathematicians have applied the theory of Finsler spaces in various fields of physics and Biology up till now. We also apply this theory to thermodynamics and ecology. |
| It is an interesting problem to find the fundamental function of a two dimensional Finsler space whose geodesics constitute a given family of curves. M. Matsumoto [5],[6],[8]1) obtained the fundamental function of a two dimensional Finsler space whose geodesics are special conic sections. The aim of the present paper is to obtain the fundamental metric function of two dimensional Finsler space whose geodesics are semi-cubical parabolas. We show that such space is locally Minkowskian. |
| PRELIMINARIES |
 |
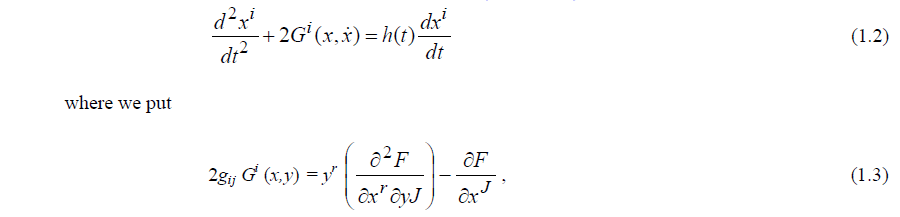 |
| and h (t) = (d2s/dt2)/ (ds/dt). |
| Now we consider two dimensional Finsler space and use the notation (x,y) and (p,q) respectively, instead of (x1,x2) and (y1,y2). The fundamental function L(x,y;p,q) are positively homogeneous of degree one in p and q. Therefore, we have |
 |
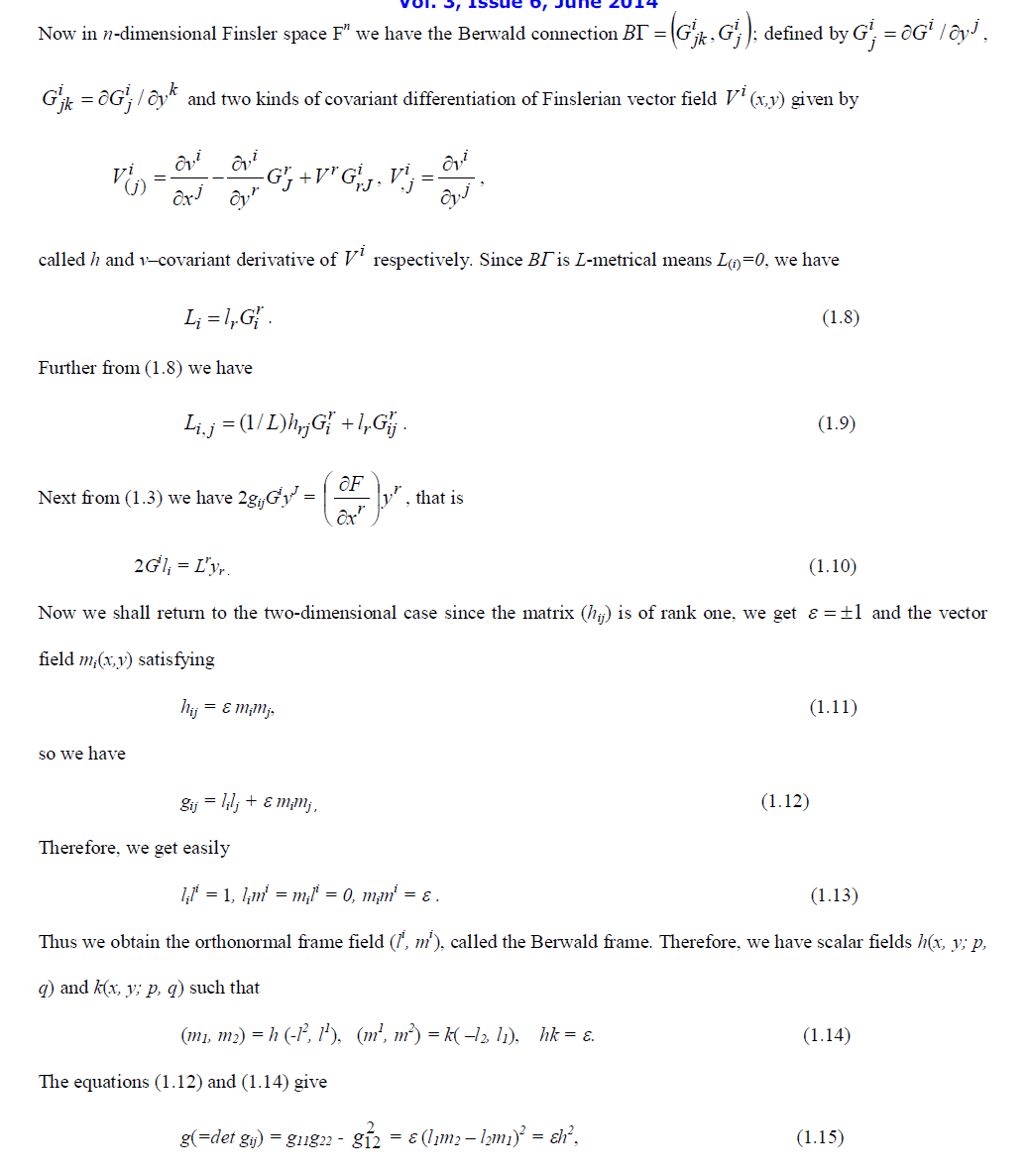 |
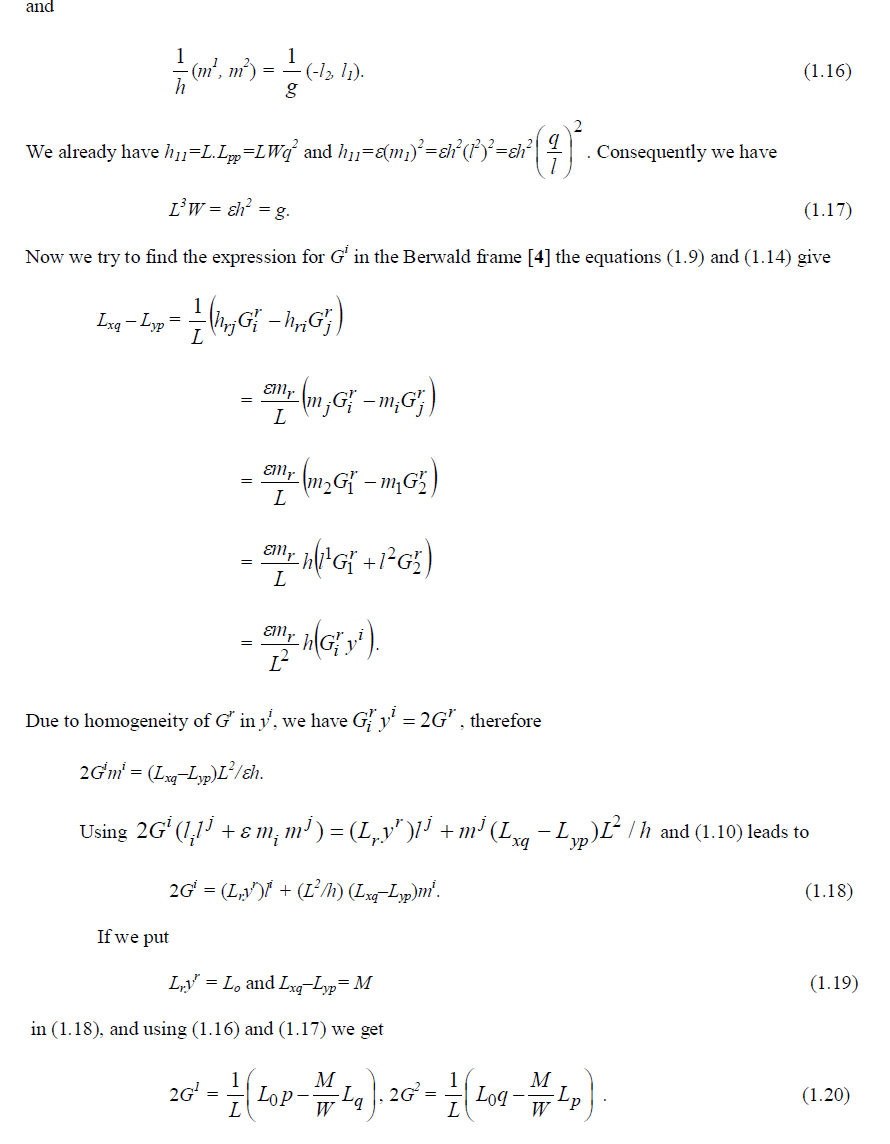 |
II. FROM GEODESICS TO THE FINSLER METRIC |
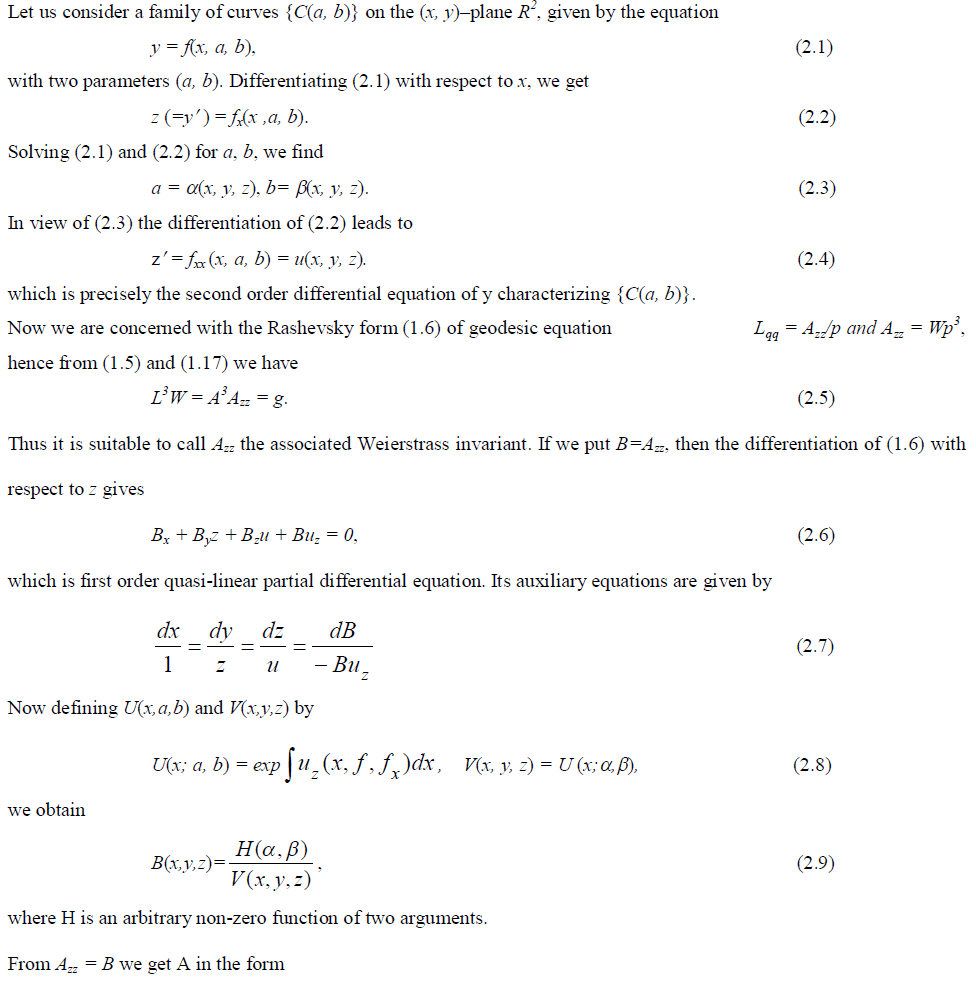 |
 |
II. FAMILY OF SEMI-CUBICAL PARABOLAS |
| Let us consider the family of semi-cubical parabolas {C(a, b)} given by the equation |
| by2 = (x – a) 3, y, b>0, (3.1) |
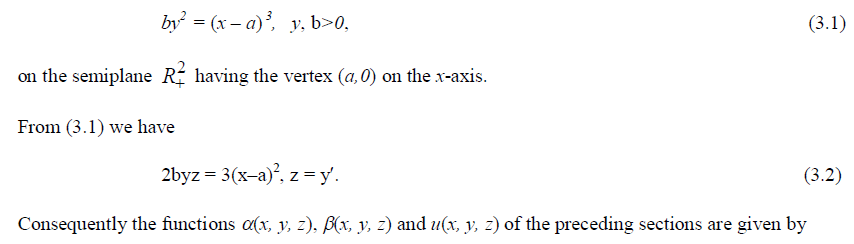 |
 |
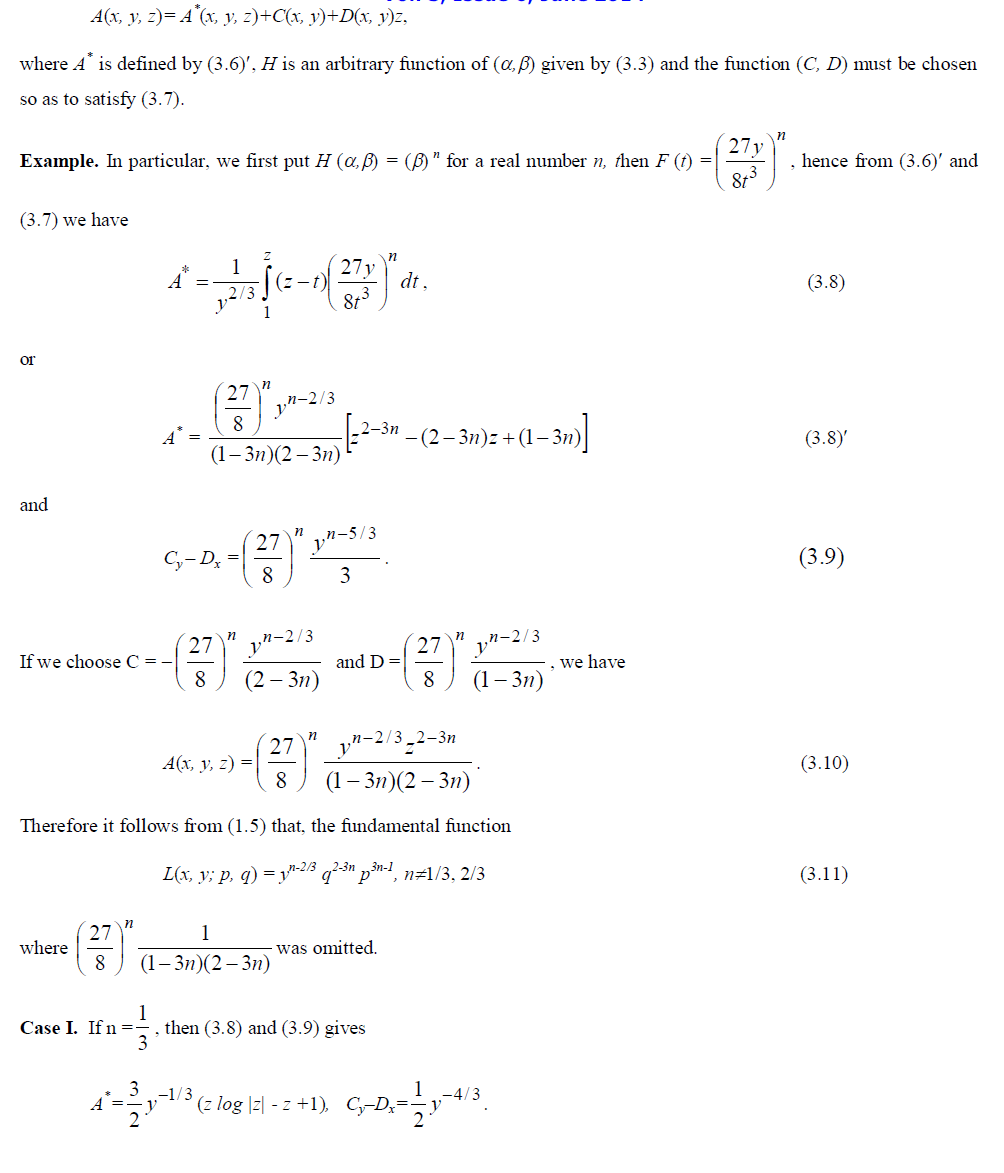 |
 |
 |
IV. CONCLUSION |
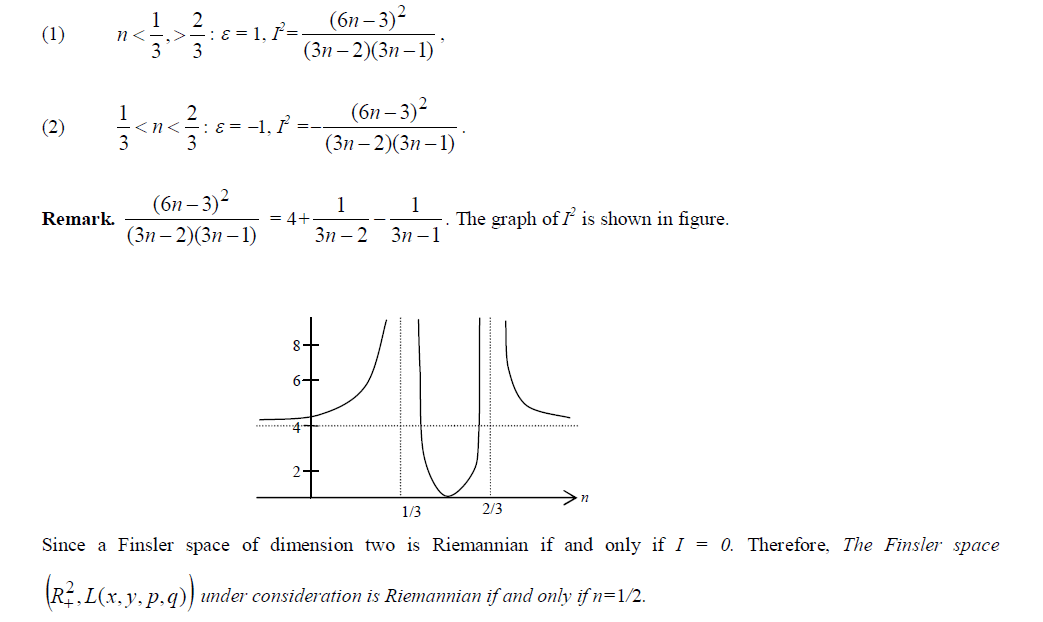
| It showed that the fundamental function of a two dimensional Finsler space whose geodesics constitute a given family of curves. We have obtained the fundamental metric function of two dimensional Finsler space whose geodesics are semi-cubical parabolas and we also proved that such space is locally Minkowskian. |
IV. ACKNOWLEDGEMENT |
| The authors are very thankful to reviewer’s valuable suggestions. |
References |
|