Research and Reviews - International Journals

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

On Fixed Point Theorem of Self Map in Fuzzy Metric Spaces

Prapoorna Manthena , M. Rangamma
Department of Mathematics, University College of Science, Osmania University, Hyderabad, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

In this paper, we prove a fixed point theorem for a self map in fuzzy metric space where the map satisfies a different condition.

Keywords
t – norm, fuzzy metric space, cauchy sequence, complete fuzzy metric space.

INTRODUCTION
The fundamental work for the fuzzy theory was first given by Zadeh [9] in 1965, who introduced the concept of fuzzy set. Kramosil and Michalek [4] developed the fuzzy metric space and later George and Veeramani [1] modified the notion of fuzzy metric spaces by introducing the concept of continuous t – norm. Many researchers have enormously developed the theory by defining different concepts and blending many properties. Fuzzy set theory has its significance in various fields such as communication, gaming, signal processing, modelling theory, image processing, etc. The purpose of this work is to prove the existence of a fixed point of a self map in fuzzy metric space (in the context of George and Veeramani [1]) by using certain condition on the mapping.

PRELIMINARIES
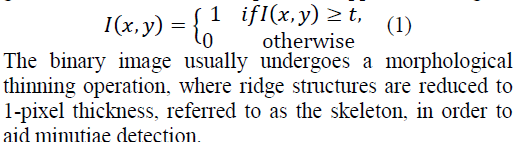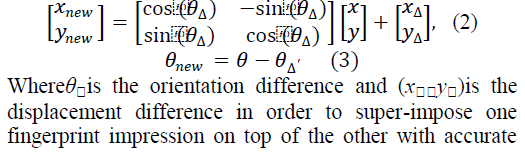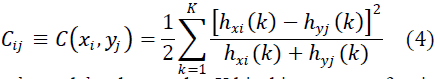image
image
image

CONCLUSION
In this article, we have proved the existence of a fixed point in a fuzzy metric space and showed that the fixed point obtained will be unique if it further satisfies an additional condition.

References
  1. George, AandVeeramani, P, “Onsomeresults in fuzzymetricspaces”, Fuzzy Sets and Systems, Vol. 64, pp. 395 – 399, 1994.
     
  2. George, A and Veeramani, P, “Onsomeresults of analysisforfuzzymetricspaces”, Fuzzy Sets and Systems, Vol. 90, pp. 365 – 368, 1997.
     
  3. Grabiec. M, “Fixedpoints in fuzzymetricspaces”, Fuzzy Sets and Systems, Vol. 27, pp. 385 – 389, 1988.
     
  4. Kramosil, I and Michalek, J, “Fuzzymetric and Statisticalmetricspaces”, Kybernetica , Vol. 11, pp. 326 – 334, 1975.
     
  5. MaggieAphane, “Onsomeresults of analysis in metricspaces and fuzzymetricspaces”, dissertation, University of South Africa, 2009.
     
  6. Mihet, D, “A Banachcontractiontheorem in fuzzymetricspaces”, Fuzzy Sets and Systems, Vol. 144, pp. 431 – 439, 2004.
     
  7. Schweizer, B and Sklar, A, “Statisticalmetricspaces”, Pacific Journal of Mathematics, Vol. 10, pp. 313 – 334, 1960.
     
  8. YonghongShen, Dong Qiu and WeiChen, “Fixedpointtheorems in fuzzymetricspaces”, AppliedMathematicsLetters, Vol. 25,pp. 138 – 141, 2012.
     
  9. Zadeh, L. A, “Fuzzy sets” , Inform. Control, Vol. 8, pp. 338 – 353, 1965.