International Journal of Innovative Research in Science, Engineering and Technology
MenuISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| Dr.Amita Joshi Assistant Professor, Department of Mathematics, IPS Acaedmy, Indore (M.P.), India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this chapter, I introduce the concept of -contractor couple in fuzzy normed spaces, which extends the concept of -contractor in fuzzy normed spaces given by Fang and Song [7]. By using the concept of -contractor couple we investigate the existence of solutions for set-valued nonlinear operator equations. As an application of our main theorem, a new fixed point theorem in fuzzy normed spaces is obtained. Our results improve and extend the results of Fang and Song [7].
Keywords |
| Fuzzy normed spaces, Φ-contractor couple. |
INTRODUCTION |
| Based on the fact that in many situations the distance between two points is inexact rather than a single real number, Kaleva and Seikkala [13] initiated the concept of fuzzy metric space by describing the distance of points as a fuzzy real number. Since each usual metric space and each Menger probabilistic metric space can be considered as a special case of fuzzy metric space, the study for the fuzzy metric space has attracted many authors and several results for nonlinear mappings have been given in some literatures [5], [10], [11], [12]. The book written by Schweizer and Sklar [16] provides a number of examples of probabilistic metric spaces, all of which are from probabilistic origin. Of course, all of which can be regarded as examples of the fuzzy metric spaces. |
| Inspired by the work of Kaleva and Seikkala [13], Felbin [8], [9] introduced and studied the fuzzy normed linear space. It is as important as the concept of Menger probabilistic normed linear space introduced by Serstnev [17] and more over, each usual normed linear space and each Menger probabilistic normed linear space can still be considered as it’s a special case. Xiao and Zhu [18] studied the linear topological structure of the fuzzy normed linear space and obtained some basic properties. Many authors proved results in fuzzy normed linear spaces including Bag and Samanta [1], Xiao and Zhu [19], [20], Fang [5], Fang and Song [7]. |
| Altman established the contractive theory in Banach spaces, which offers a strong tool to study the existence and uniqueness of solutions for nonlinear operator equations. Inspired by Altman's work, Lee and Padgett [14], [15] studied the random contractive theory and showed the existence and uniqueness of solution for random operator equations with a random contractor. Chang [2] and Chang et al. [3], [4], Fang [6], Zeng [21] studied the probabilistic contractive theory in Menger probabilistic normed spaces and discussed the existence and uniqueness of solutions for operator equations with the probabilistic contractors. |
PRELIMINARIES |
 |
 |
 |
 |
 |
 |
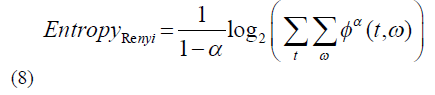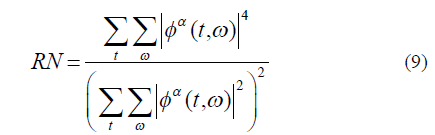CONCLUSIONS |
| Fang and Song [7] defined Φ-contractor in fuzzy normed spaces. In this paper, we have extended the concept of Φ- contractor and defined Φ-contractor couple in fuzzy normed spaces. With the help of Φ-contractor couple we have proved the existence theorem of solutions for set-valued nonlinear operator equations in fuzzy normed spaces. We have applied our existence theorem to prove a new fixed point theorem in fuzzy normed spaces. Many questions are raised by this work. First one such, the examination of the conditions which enable one to easily apply the existence theorem and fixed point theorem, we have discussed, which are mostly stated as purely mathematical results. The second question of which our theorems can give constructive proofs. Other questions can be posed and indeed all are under investigation and will be considered elsewhere. |
References |
|