ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Reuben Jacob, V. Malathi
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
This paper presents a new method to solve the network reconfiguration problem. The uncertainty of system loads on different feeders which vary from time to time makes the distribution system operation and its control more complex. For a fixed network configuration power loss is not minimum in a distributed network. Hence, there is a necessity for reconfiguration of the network. Network reconfiguration is the process of altering the topological plan of feeders by changing switching status of sectionalizing and tie switches. Reconfiguration is carried out generally to reduce real power loss and to prevent overload in the network. Since network reconfiguration is a complex combinatorial optimization problem with several constraints, many algorithms are proposed in the past. The integrated approach for reconfiguration of power distribution systems helps to obtain more efficiency on power distribution systems with improved voltage profile. This paper introduces one of applications of the Ant Colony Optimization (ACO) technique to solve the optimal network reconfiguration problem. The proposed method was examined on distribution network consisting of 33- bus radial distribution systems at different load levels to evaluate the performance and effectiveness of the proposed method.
Keywords |
| Distributed network, reconfiguration, real power loss, efficiency, voltage profile, Ant Colony Optimization. |
INTRODUCTION |
| There are numerous switches on distribution system in general. These switches are divided into two types: sectionalizing-switches (normal closed) and tie switches (normal open). By changing the on/off status of distribution feeder switches, or feeder reconfiguration, loads can be transferred from on feeder to an adjacent feeder to redistribute loads. Feeder reconfiguration can be used to maintain system balance, reduce feeder losses and improve system reliability. |
| Distribution systems are normally configured radially. From time to time, modifying the radial structure of the feeders by changing the ON/OFF status of the sectionalizing and tie switches to transfer loads from one feeder to another may significantly reduce the distribution losses. Distribution system normally has a combination of industrial, commercial, residential and lighting loads. So, the peak load on the substation and feeders occurs at different times of the day, the systems become heavily loaded at certain times of the day, and lightly loaded at some other times. If the distribution loads are rescheduled more efficiently by network reconfiguration, improved efficiency of distribution system can be achieved. Reconfiguration play important role in smoothening out the peak demands, improving the voltage profiles at the buses. Ideally, losses in an electric system should be around 3 to 6%. In developed countries it is not more than 10%. However, in developing countries like India, the percentage of active losses is around 20%; therefore the utilities in the electric sector are presently interested in reducing it in order to have an edge in the competition; since the electricity prices in the de- regulated markets are related to the system losses. In India, collective of all states, in 2012 the technical and non- technical losses are accounted as 23% of the total input energy. In order to manage a program for loss reduction in a transmission and distribution system, it is necessary to use efficient and effective computational tools like MATLAB. |
| In this paper the concept of network reconfiguration is successfully implemented in the existing real life electric distribution networks at different load levels with the help of above mentioned tool for implementing the Ant Colony Optimization (ACO) for reconfiguration of 33-bus radial distribution system. When implemented it shall reduce both the transmission line active and reactive power losses substantially and enhance the voltage stability of the system as well. |
| They are difficult to solve by traditional linear or nonlinear programming methods. Therefore, the Ant Colony Optimization algorithm has been utilized in this paper to find an optimum solution. The characteristics of the ACO algorithm consists of positive feedback, computation with distributed nature, and a constructive heuristics. The positive feedback characteristics make sure of a rapid search for a global solution; distributed computation avoids premature convergence, and constructive greedy heuristics help find acceptable solution as soon as possible. These properties are counterbalanced by the fact that, for some applications, the ACO can outperform other heuristics. The main advantage of this paper is to propose a novel feeder reconfiguration technology based on the ACO algorithm. In general, the ACO algorithm is a useful evolutionary algorithm with strong global search ability. Its positive feedback would account for rapid discovery of good solutions in comparison to GA (Genetic Algorithm). Therefore, the proposed method in this paper can provide another useful algorithm for the feeder reconfiguration. |
| Objective is to study about the 33 bus radial distribution system reconfiguration for power loss minimization and to introduce Ant Colony Optimization (ACO) algorithm to get optimized reconfiguration status of the sectionalizing and the tie line switches. Also compare the performance of ACO results with the Harmony Search Algorithm (HSA) results. |
| Many researchers studied the feeder reconfiguration problems using different methods in the past decades. The results of these researches provide acceptable solutions for feeder reconfiguration problems. In order to minimize power losses and improve the searching speed heuristic methods were proposed in [1]. Soft computing approaches were also applied to the problem extensively, for example, neural network [2], Simulated Annealing (SA) [3], Genetic Algorithm (GA) [4, 5] and Evolutionary Programming (EP) [6]. Algorithms based on concept of mimicking swarm intelligent are popular in recent years. For instance, Ant Colony Optimization (ACO) [7] and Particle Swarm Optimization (PSO) [8] are the algorithms that can be applied to the field of optimization problems. |
| Since network reconfiguration is a complex combinatorial optimization problem consist of several constrains, many algorithms are introduced in the past. Merlin and Back [1] first proposed network reconfiguration problem and they used a branch and bound-type optimization technique. The main drawback deals with this technique is the solution proved to be very time consuming as the possible system configurations are, where line sections equipped with switches is based on the method of Merlin and Back [9], a heuristic algorithm has been suggested by Shirmohammadi and Hong [10]. The drawback with this algorithm is simultaneous switching of the feeder reconfiguration is not considered. Civanlar [11] suggested a simple formula along with heuristic algorithm support was developed to determine change in power loss due to an exchange of branches. The disadvantage of this simple approach is only one pair of switching operations is considered at a time and reconfiguration of network depends on the initial switching status. Das [12] presented an algorithm based on the heuristic rules and fuzzy multi-objective approach for optimizing configuration of network. The problem in this method is criteria for selecting membership functions for objectives are not provided. Nara [13] presented a solution using a Genetic Algorithm (GA) to look for the minimum loss configuration in distribution system. Zhu [14] presented a Refined Genetic Algorithm (RGA) to reduce losses in the distribution system. While considering RGA, the conventional crossover and mutation schemes are refined by a competition mechanism. Rao [15] proposed Harmony Search Algorithm (HSA) to solve the network reconfiguration problem to get optimal switching combinations simultaneously in the network to minimize real power losses in the distribution network. The strong global search ability and positive feedback with heuristic performance of ACO algorithm makes us to prefer it over other heuristics. |
| The ACO counterbalanced by the fact that, for some applications, the ACO can outperform other heuristics. In the proposed work ACO is preferred for the reconfiguration of power distribution systems and the obtained result is compared with the HSA [16] results. |
| The section wise summary of the paper is as follows: section II discusses about problem formulation. Section III covers the basics of ACO algorithm. Section IV results are compared and discussed in this section. Then output of reconfigured network using ACO is compared with base case result at different load levels and with HSA results and over all discussions towards conclusion. Section V presents the conclusion and scope of future work of the paper. |
II. PROBLEM FORMULATION |
A. Power Flow Equations |
| Power flows in a distribution system are computed by the following set of simplified recursive equations [19] derived from the single-line diagram shown in Fig.1. |
 |
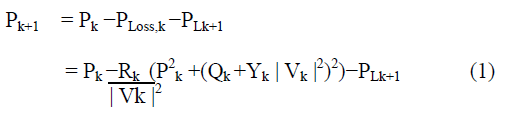 |
 |
C. Distribution Feeder Model |
| Fig.2 shows a simple feeder of a distribution system consisting of several main and lateral sections, and the feeder load can be partially supplied by an interconnection of neighbouring feeders. The distribution feeder can be represented by a tree graph in which node oi corresponds to tap connections or load points [20]. Since each edge has a unique end node in the tree graph, the edge (oi, oj) can be denoted as edge j. It corresponds to section j of the distribution system. Let s (i) be the immediate predecessor of edge i. The set of predecessors for edge i is defined as the following equation: |
| Si = (i, s(i), s(s(i)), s(s(s(i))), ...) |
| Si, the section path, contains all sections belonging to the path that connects section i to the energy source. For a simple distribution feeder in Fig.4, the paths connecting sections 10 to the source are described as follows: |
| S10 = 10,7,3,1 |
 |
III. ANT COLONY OPTIMIZATION- AN OVERVIEW |
A. History |
| Invented by Marco Dorigo in 1992, Ant Colony Optimization (ACO) is a meta-heuristic stochastic combinatorial computational discipline inspired by the behaviour of ant colonies which belong to a family of meta-heuristic stochastic methodologies such as Simulated Annealing (SA), Tabu Search and Genetic Algorithms (GA). It is a iterative method in which populations of ants act as agents that construct bundles of candidate solutions, where the entire bundle construction process is probabilistically guided by heuristic imitation of ant‘s behaviour, tailor-made to the characteristics of a given problem. Since its invention ACO was successfully applied to a broad range of Non linear Programming (NP) hard problems such as the Travelling Salesman Problem (TSP) or the Quadratic Assignment Problem (QAP), and is increasingly gaining interest for solving real life engineering and scientific problems. |
B. Ideology |
| The ant colony algorithm imitate of real ants. It is well known that real ants are capable of finding the shortest path from food sources to the nest using their visual cueing mechanism. Also, they are very much capable of adapting to changes in the environment; consider an example to find a new shortest path once the old one is no longer feasible due to a new obstacle. Moreover, the ants could manage to establish shortest paths through the medium that is called ―pheromone‖. The pheromone is the material deposited by the ants, which serves as critical communication information within ants, guiding thereby the determination of the next movement. Ant trial that is rich of pheromone will thus become the goal path. The process is illustrated in Fig.1. The ants are in motion from food source ‗A‘ to the nest ‗B‘ on a straight line in Fig.1 (a). Once an obstacle appears as shown in Fig.1 (b), the path is cut off. The ants will not be able to follow the original trail in their motion. Under this situation, they have equal probability to turn right or left. Fig.1 (c) depicts that the shorter path will collect larger amount of pheromone than the longer path. Hence, more ants will be increasingly guided to move on to the shorter path. By this autocatalytic process, quickly all ants will choose the shorter path. As illustrated in Fig.3, by the guidance of the pheromone intensity, the ants select preferable path. At first, each ant is placed on a starting phase. Each will build a full path, from the beginning to the end phase, through the repeated application of state transition rule. |
 |
| While constructing its tour, an ant also modifies the amount of pheromone on the visited path by applying the local updating rule. Once all ants have terminated their amount of pheromone on edge is modified again through the global updating rule. In other words, the pheromoneupdating rules are designed so that they tend to give more pheromones to paths which should be visited by ants. In the following the rules of state transition, local updating and the global updating are briefly introduced [17]. |
C. State transition rule |
| The state transition rule used by the ants system is a random proportional rule which is given by (7), which gives the probability with which ant k in node i chooses to move to node j. |
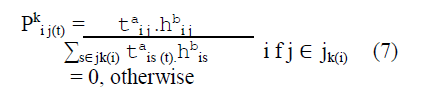 |
| Where t is the pheromone which deposited on the edge between nodes i and j, h the inverse of the edge distance, jk(i) the set of nodes that remain to be visited by ant k positioned on node i, a is the weight of the pheromone concentration and b is a parameter that determines the relative importance of pheromone versus distance. Equation (7) indicates that the state transition rule favours transition toward nodes connected by shorter edges and with greater large amount of pheromone. |
D. Updating rule |
| While considering its tour, all ants modify their pheromone by the local updating rule. This can be written below: |
| t (i, j) = (1−r)t (i, j)+rt0 |
| That t0 the initial pheromone has a value and r is a heuristically defined parameter the local updating rule is intended to shuffle the searching process. So the desirability of paths can be dynamically changed. The nodes visited earlier by a certain ant can be explored later by other ants also. Therefore the search space can be extended. Furthermore, in so doing, ants will make a better use of pheromone information. Without local updating, all ants would search in a narrow neighbourhood of the best previous tour. |
E. Global updating rule |
| When tours are completed, the global updating rule is applied to edges belonging to the best ant tour. This rule is intended to provide a greater amount of pheromone to shortest tour, this can be expressed below: |
| t (i, j) = (1−δ )t(i, j) + sδ −1 |
| That δ is the distance of the globally best tour from the beginning of the trial and s v [0,1] is the pheromone decay parameter. This rule is intended to make the search more directed; therefore the capability of finding the optimal solution can be enhanced through this rule in the problem solving process [17] |
F. Proposed method |
| The computational procedures of the proposed method are mainly composed of power-loss calculation, bus voltage determination and ant colony application. The computational procedures find a series of configuration with different status of switches such that the objective function is successively reduced. The objective function of the problem can be described as: |
| minF = min(PLoss) (10) |
| At first, the colonies of ant are randomly selected and the initial fitness in different permutations was estimated. The initial pheromone value t0 of is also given at this step. Then, the fitness of ants, which is defined as objective function, is estimated and the pheromone can be added to the particular direction in which the ants have chosen. In this time, by roulette selection method, fitness with higher amount of pheromone will be easy to find. The ants of reconfiguration are based on level of pheromone and distance. A greater t(i, j) means that there has been a lot of traffic on this edge; hence it is proportional to loss inversion and a greater h(i, j) indicates that the closer node should be chosen with a higher probability. In the network reconfiguration study, this can be seen as the difference between the initial total power loss and the new total power loss. |
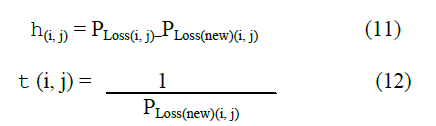 |
| While constructing a solution of the reconfiguration problem, ants visit edge and change their pheromone level by local updating rule of (8). After n iteration, all ants have completed a tour; the pheromone level is updated by applying the global updating rule of (9) for the trial that belongs to the best selected path. Therefore, according to this rule, the shortest path found by the ants is allowed to update its pheromone. Also, this shortest path will be saved as a record for the later comparison with the succeeding iteration. |
| Then, if all ants have selected the same tour, the process is satisfactory and acceptable; otherwise, repeat the outer loop. In reconfiguration problem some constrains should be considered: |
| • Distribution network should not lose its radial structure. |
| • All nodes should be energized. |
| • Voltage magnitude at each node must be kept within their permissible range. |
IV. RESULTS AND DISCUSSION |
| This test system is a 33-bus radial distribution system [15] with five tie- switches and 32 sectionalizing switches. In the network, sectionalize switches (normally closed) are numbered from 1 to 32, and tie-switches (normally open) are numbered from 33 to 37. The Table 1 consist of line and load data of network are taken from [1], and the total real and reactive power loads on the system are 3715 kW and 2300 kVAR. ACO is applied to test systems consisting of 33 buses. In the simulation of network, two scenarios are considered to analyze the superiority of the proposed method. |
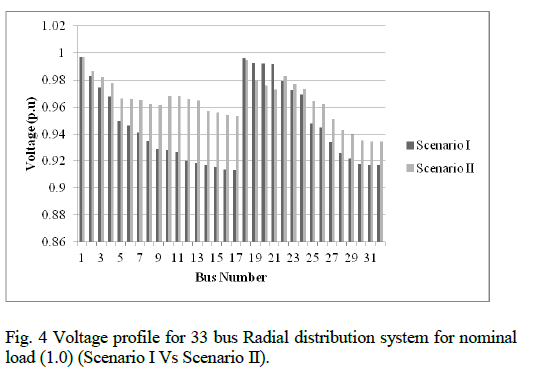
| Scenario I: The system is without reconfiguration (Base case); Scenario II: Same as Scenario I except that system is reconfigured by the available sectionalizing and tie switches using HSA; Scenario III: Same as Scenario I except that system is reconfigured by the available sectionalizing and tie switches using ACO. The reconfiguration result obtained [15] by using HSA at different load levels, that is light, nominal and heavy is given in Table.1. The improved voltage profile is compared in Fig 4. The voltage profile improvement along with power loss minimisation is obtained using HSA. There is a 29.3, 31.88 and 33.86 percentage loss reduction in light, nominal and heavy load levels respectively. |
 |
| A. ACO results |
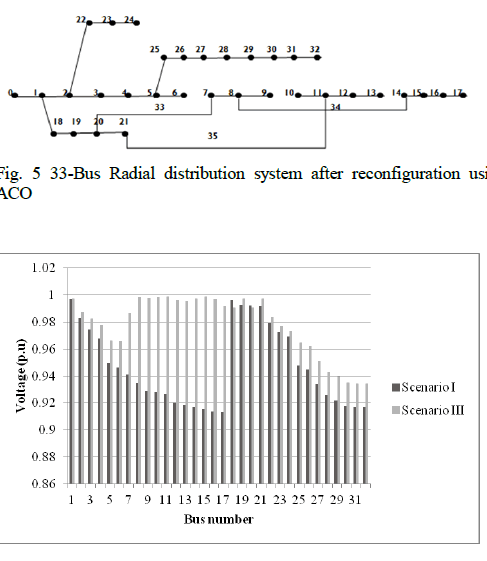
| The ACO simulation parameters are weight of pheromone concentration a = 1.0, relative importance of pheromone updation b = 2.0, evaporation coefficient r = 0.2, initial pheromone t0= 0.0001, pheromone decay parameter s = 0.96, number of cycles, iteration = 100, number of ant, M = 200.The section switches and the tie line switches to be opened are obtained as 7, 10,14,36,37. With the above obtained results the reconfigured 33 bus distribution system after considering the switches to be opened is shown in Fig.5 |
 |
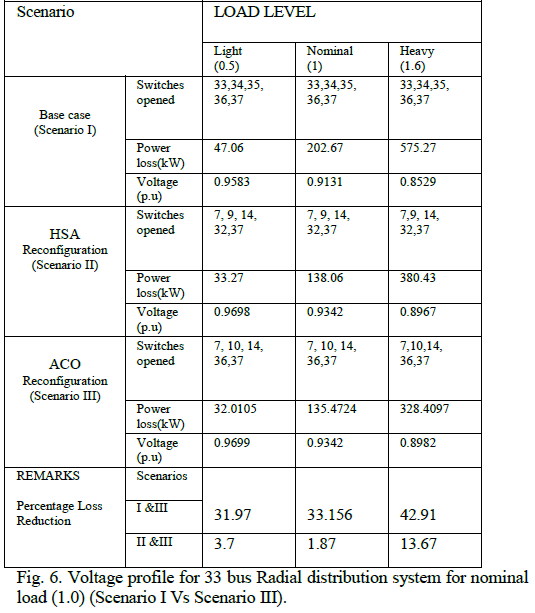 |
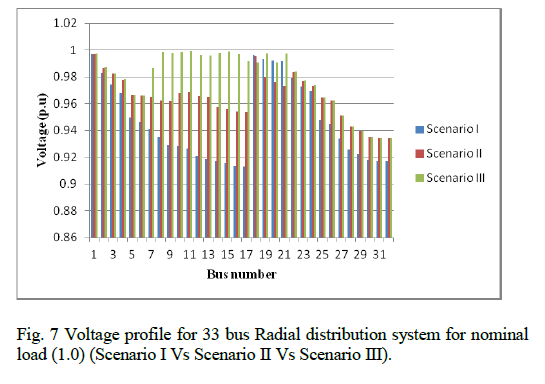
| The reconfiguration result obtained by using ACO at different load levels, that is light, nominal and heavy of all the three scenarios are compared in Table.1. The improved voltage profile is compared in Fig 6. The voltage profile improvement along with power loss minimisation is obtained with ACO. Overall comparison of voltage profile of all the three scenarios are performed in fig 7. |
 |
V. CONCLUSION |
| In this paper an efficient ACO method is proposed, which is of positive feedback makes sure of a rapid search for achieving the global solution. Computation in distributed manner avoids premature convergence and constructive heuristics help to find acceptable solution as soon as possible. These properties are counterbalanced by the fact that, for some applications, the ACO can outperform other heuristics is stated. The effectiveness of the developed algorithm is tested for 33-bus distribution network at varying load. The following conclusions are drawn from the study. |
| • Method can outperform HSA algorithm and gives better result. |
| • The percentage of power loss reduction is achieved above 30% than the base case at different load levels. |
| • It also has positive effect on voltage profile. Nowadays, distributed generation have an effective role in power distribution networks. Typically 5-kW to 10-MW capacities of DG (Distributed Generation) units is installed nearer to the end-user to provide the electrical supply. Since the selection of best locations and sizes of DG units is also a complex combinatorial optimization problem. Sensitivity analysis is used to compute sensitivity factors of candidate bus locations to install DG units in the system. Proper estimation of these candidate buses helps in reduction of the search space for the ACO procedure. |
References |
|