International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Optimal Sizing Of Distributed Generation For Voltage Profile Improvement Considering Maximum Loadability Limit

Dr.K.Gnanambal#1, S.Suriya*2
  1. Professor, Department of Electrical and Electronics Engineering, K.L.N College of Engineering, Sivagangai, India.
  2. P.G.Scholar (M.E.Power System Engineering, Department of Electrical and Electronics Engineering, K.L.N College of Engineering, Sivagangai, India.
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Nowadays power demand is the major problem in the electricity market. Distributed Generation (DG) is becoming more important in the power system because of its high efficiency. This paper is concerned with the Differential Evolution Algorithm for the optimal sizing of Distributed Generation. The objective is minimization of DG cost and maximization of the loadability value. The improvement of voltage profile is also considered. IEEE-14 bus system and 34 bus Radial Distribution System are considered to test the effectiveness of the DE for optimal sizing of DG with maximizing the loadability and minimizing the DG cost.

Keywords
Distributed Generation (DG), Economic Dispatch (ED), Optimal Power Flow (OPF), Differential Evolution (DE), Maximum Loadability Limit.

INTRODUCTION
Distributed Generation is a small power generating unit that is usually connected to the distribution system. It is also known as Embedded Generation (EG) or Dispersed Generation (DG). Distributed Generation (DG) which consists of distributed resources, can be defined as electric Power generation within distribution networks or on the consumer side of the network [1]. DG impacts on distribution system depends on several factors such as DG location, capacity of DG and the mode of DG operation with network [2]. DG is an emerging approach for providing electric power to the power system.
The penetration and viability of DG at a particular location is influenced by technical as well as economic factors. The technical merits of DG implementation include voltage support, energy loss reduction, and release of system capacity and improve utility system reliability[3]. Two methodologies for optimal placement of distributed generation (DG) in an optimal power flow based wholesale electricity market were presented in [3]. The minimization of cost and loss with the maximum potential benefit was suggested in [4]. The formulation of three phase optimal power flow with the control variables (actual active load demand and reactive power outputs of micro generators) was presented in [5].The analytical methods to determine the optimal location of DG in radial distribution networks for loss minimization in the power system is proposed in [6]. Particle Swarm Optimization algorithm (PSO) for the optimal placement and sizing of DG units in order to reduce network congestion was presented in [7] .One of the most powerful evolutionary algorithm is Differential Evolution (DE) because of its excellent convergence characteristics and a few control parameters. The computational algorithm of DE is simple to understand and implement. Only a few parameters are required to be set by the users [9-11].
The maximum loadability limit is the margin between the operating point of the system and the maximum loading point that can be formulated as an optimization problem.
This paper concentrates the voltage profile improvement by placing the DG with the constraint of maximizing the loadability and minimizing the DG cost by using Differential Evolution Algorithm.

II. OVERVIEW OF THE PROPOSED IDEA
Fig.1. represents the overview of the paper. Optimal location of DG is determined by using the Differential Evolution algorithm. After the location of DG by changing the DG penetration level the minimization of DG cost and the maximization of the loadability is done by using the DE.
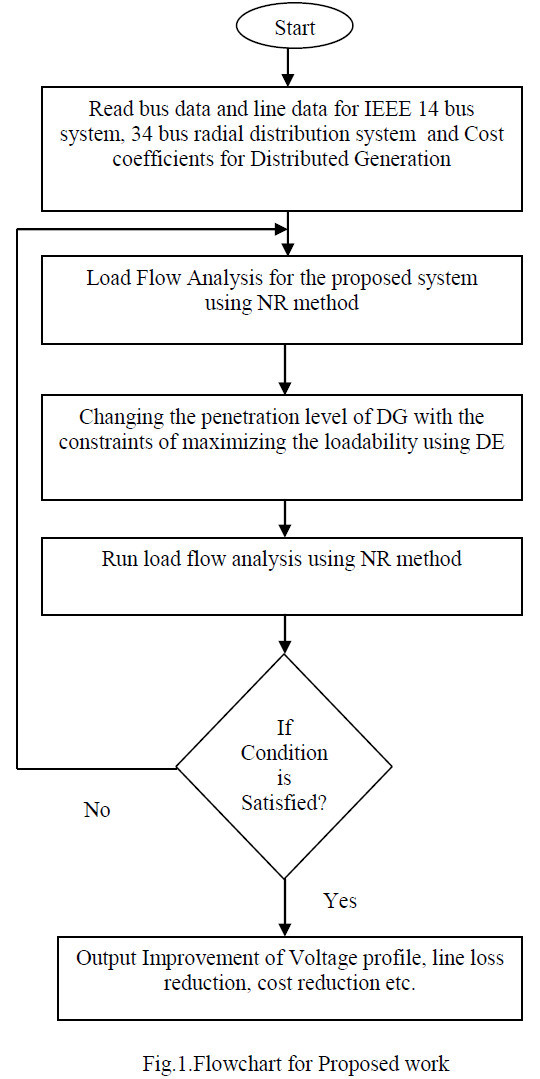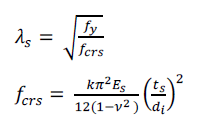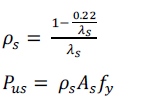image
image
image

IV. OVERVIEW OF DIFFERENTIAL EVOLUTION
As a relatively new member of EAs, DE is less known outside meta heuristic optimization area. Similar to other EAs, DE relies likewise on the initial population generation, mutation, recombination and selection to probe search space through iterative progress until the terminate criteria are met. [12]
Main operators for DE: The performance of DE is mainly dependent on three operators, mutation, recombination and selection. Detailed discussion of them is presented accordingly in the sequel.
Mutation: The function of mutation in DE is to maintain the diversity of population as well as provide necessary information to steer the optimization. A typical DE mutation formulation is
image
Clearly (5) is a linear combination of two vectors and the resulting mutation becomes an arithmetic crossover process.
Recombination: Recombination or crossover is the main operator for GAs but only a complementary process for DE. The basic recombination process is a discrete recombination, which employs a constant C R € [0, 1] to determinate if the newly generation individual is to be recombined. Alternatively, the arithmetic crossover formula of (5) can be used to achieve the rotational invariance which is otherwise difficult to be achieved with the discrete recombination. The resulting expression of the mutation and crossover processes are given in (10) as a combination of (8) & (9)
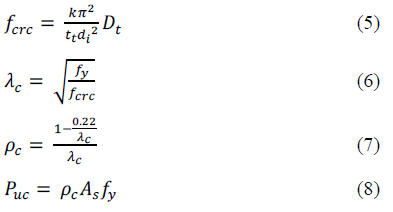image

V.RESULTS AND DISCUSSION
The proposed DE algorithm is applied to determine the optimal location and sizing of DG with the constraint of maximizing the loadability have been conducted under MATLAB 12 environment.
The test system used to demonstrate the paper work is,
 IEEE 14 bus system.
 34 bus Radial Distribution System.

A.IEEE 14 BUS SYSTEM
The standard IEEE-14 bus system consists of 6 generator bus, 9 load buses and 20 transmission lines. The generator buses are 1, 2, 3, 6 and 8 with the slack bus connected to node 1. The other nodes are connected to all other nodes. The optimal location and sizing of DG will takes place at all load buses.
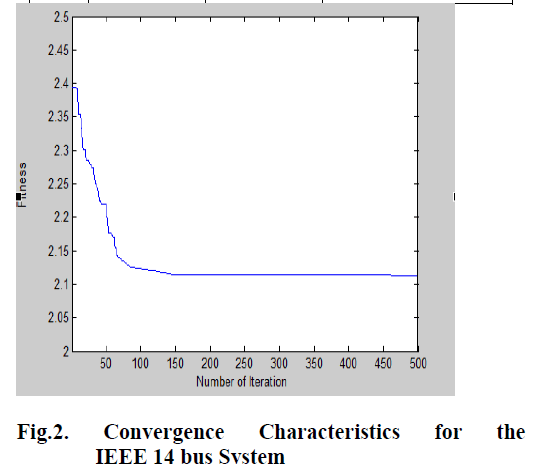
The voltage profile improvement for the IEEE 14 bus system with DG and without DG using Differential Evolution (DE) is discussed in Table 1.
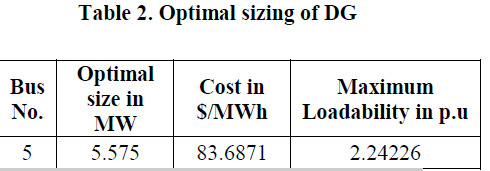
Optimal Sizing of DG will takes place on load buses and determine the best optimal location and DG size with the constraint of maximum loadability and minimizing DG Cost that will be discussed in Table2.
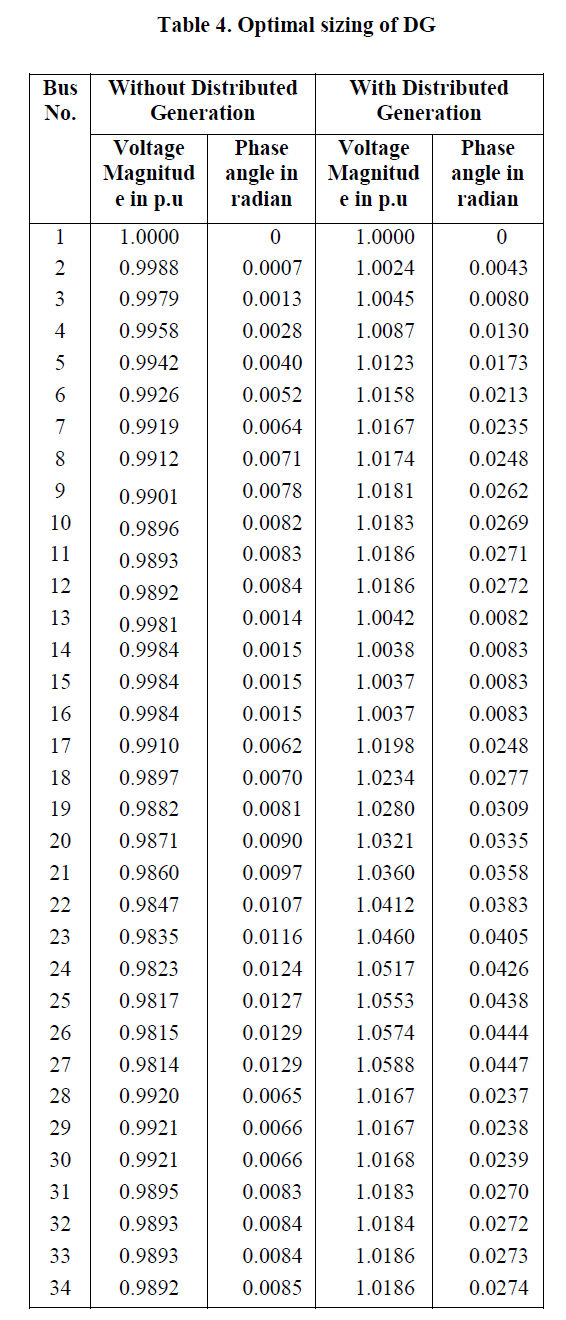
image
image
image
B.34 bus Radial Distribution System The second test case for the proposed method is a 34 bus radial distribution system.This system consists of main feeder and four laterals. The line and load data are taken from reference.
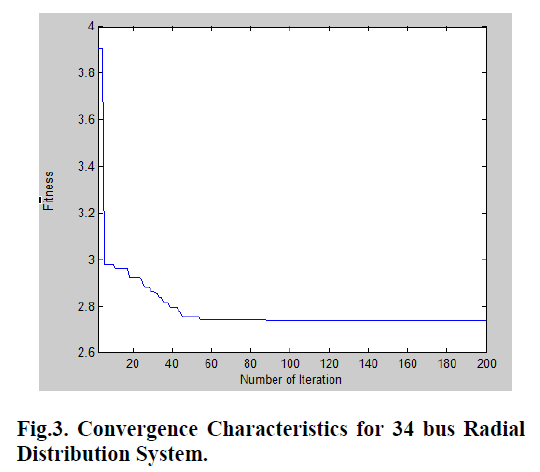
The voltage profile improvement for the 34 bus system with DG and without DG by using Differential Evolution (DE) is discussed in Table 3.
Optimal Sizing of DG will takes place on minimum voltage buses and determine the best optimal location and DG size with the constraint of maximum loadability and minimizing DG Cost that will be discussed in Table 4.
image
image
image

VI CONCLUSION
This paper presented a method for optimal sizing of DG to improve maximum allowable load in the distribution system. Differential Evolution algorithm has been proposed for the optimal sizing of DG. IEEE 14 bus system and 34 bus radial distribution system are considered to test the effectiveness of DE.
image

References
  1. J.A. Pecas Lopes, N.Hatziagyriou, J.Mutale, “Integrating distributed generation into electric power systems: A review of drivers, challenges and opportunities”, Electric Power System Research 77 (2007), pp.1189-1203.
  2. K.Balamurugan, Dipti Srinivasan, Thomas Reindl, “Impact of Distributed Generation on Power Distribution Systems”, Energy Procedia 25(2012) 93-100.
  3. Durga Gautam and Nadarajah Mithulananthan, “Optimal DG placement in deregulated electricity market”, Electric Power Systems Research 77 (2007) , pp. 1627-1636.
  4. Sudipta Ghosh , S.P.Ghoshal, and Saradindu Ghosh , “Optimal sizing and placement of distributed generation in a network system”, Electrical Power and Energy Systems 32(2010) 849- 856.
  5. Sergio Bruno, Silvia Lamonaca, Giuseppe Rotondo, Ugo Stecchi, and Massimo La Scala , “Unbalanced Three-Phase Optimal Power Flow for Smart Grids”, IEEE Transactions on Industrial Electronics, vol.58, No.10, October 2011.
  6. N.Acharya, “An Analytical Approach for DG Allocation in Primary Distribution Network”, Elsevier Journal of Electrical Power and Energy Systems, vol.28, pp.669-678, 2006.
  7. Seon-Ju Ahn, Soon-Ryul Nam, Joon-Ho Choi and Seung-II Moon, “Power Scheduling of Distributed Generators for Economic and Stable Operation of a Microgrid”, IEEE Transactions on Smart Grid, vol. 4, No.1, March 2013.
  8. Monica Alonso, Hortensia Amaris and Carlos Alvarez-Ortega, “Integration of renewable energy sources in smart grid by means of evolutionary optimization algorithms”, Expert Systems with Applications 39(2012), pp. 5513-5522.
  9. Chung-Fu Chang, Ji-Jen Wong, Ji-Pyng Chiou and Ching-Tzong Su, “Robulst searching hybrid differential evolution method for optimal reactive power planning in large scale distribution systems”, Electric Power Systems Research, Vol 77, pp. 430- 437, April 2007.
  10. Cai, H.R. Chung, C.Y.Wong, K.P. “Application of Differential Evolution Algorithm for Transient Stability Constrained Optimal Power Flow”, IEEE Transactions on Power System Vol 23, pp 719-728, May 2008.
  11. Xiaohui Yuan, Anjun Su, Hao Nie, Yanbin Yuan and Liang Wang, “Application of enhanced discrete differential evolution approach to unit commitment problem”, Energy Conversion and Management, Vol 50, Issue 9, pp 2449-2456, Sept 2009.
  12. Guang Ya Yang, Zhao Yang Dong and Kit Po Wong, “A Modified Differential Evolution Algorithm with Fitness sharing for Power System Planning”, IEEE Trans. on Power Systems, Vol 23, pp. 514-522. May 2008