ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
S.Venkatesan 1, J.Senthil kumar2, T.S.Manipriya3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The major problem of System Operator (SO) is to utilize the generated power effectively without disturbing the reliability of the market. This paper proposes a methodology to identify the reliable wheeling transaction in hybrid power market by performing Particle Swarm Optimization (PSO) based Optimal Power Flow (OPF). The customer location is selected based on Locational Marginal Price (LMP). The new generation schedule for all generator buses are computed by PSO with an objective of increasing the system performance by optimizing the generation cost. Based on the power transfer capability the transaction is suggested for the Independent Power Producer (IPP) in deregulated environment. The proposed frame work is illustrated with IEEE-30 bus system and Indian utility 69 bus system.
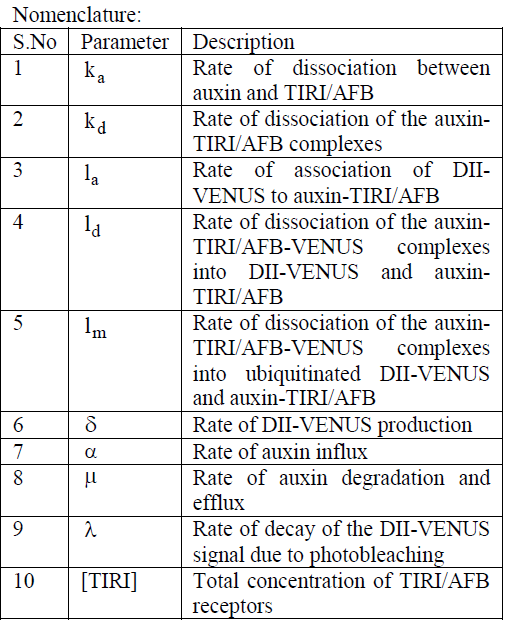
Keywords |
| Independent Power Producer (IPP), Independent System Operator (ISO), Locational Marginal Price (LMP), Optimal Power Flow (OPF), Particle Swarm Optimization (PSO), Wheeling transaction. |
INTRODUCTION |
| Competition in deregulated power market has given rise to the increased power suppliers and the constantly increasing population also increased the power demand all over the world. In deregulation environment transmission and distribution are independent activities [1]. The main benefit of deregulation include cheap electricity, efficient capacity, expansion planning and provides more choice for better services. ISO is authorized to set rules for transaction between suppliers and consumers, scheduling |
| and dispatch of generators and loads in energy markets. The role ISO to provide power at low cost without disturbing the reliability of system becomes the tedious job. When the producers and consumers of electric energy desire to produce and consume in amounts that would cause the transmission system to operate at or beyond one or more transfer limits, the system is said to be congested. |
| Methods are proposed to minimize the curtailment of the contracted powers in a power market in case of congestion by using optimal power flow model and for the optimal allocation of distributed generators considering congestion relief and voltage security in deregulated environment [2-3]. The congestion zones are identified by transmission congestion distribution factor to reschedule the generators in that zone [4]. The hybrid power market is a combination of best features of pool market and bilateral market, in a hybrid power market; market participants can buy/sell electric energy from the spot market and can also sign long-term bilateral contracts to reduce their price risk [5]. In the spot market, suppliers submit their generation bids and customers submit their demand bids to the power pool. For a bilateral transaction, energy price is agreed by two contracted parties, and the contracted quantity and locations are provided to the ISO. If there is no violation of static and dynamic security, the ISO simply dispatches all requested transactions and charges for the service [6]. |
| The bilateral transaction provides the motivation of transaction between Independent Power Producer (IPP) and consumers. An IPP consist of one or more generating units within a single company ownership connected together to produce and sell electricity. The major objective of an IPP is to sell the power at beneficial cost without disturbing the reliability of the system [7]. |
| Wheeling is the transmission of electrical energy from a seller to buyer through a transmission network owned by a third party [8]. The wheeling utility is paid for its service and for meeting the losses. It might require rescheduling its own generation, because of wheeling transactions. The reasonable price is provided for load prices and wheeling charges by considering the recovering of expense from utilities [9]. The impacts of wheeling on deregulated environment are studied by considering the transmission loss, voltage profiles and network congestion [11]. |
| The economic dispatch optimization has been computed to reduce the number of participating generators and optimum rescheduling of their output while managing congestion in a pool at minimum rescheduling cost [13]. A wide variety of optimization techniques have been applied in solving the OPF problems. PSO technique used to minimize the deviation of rescheduled value of generator power outputs from scheduled levels [15]. The economic dispatch optimization can be formulated using OPF with PSO [16]. OPF is proposed to find the optimal setting of a power system network that optimize certain objective function when satisfying its power flow equations and equipment operating limit. |
| LMP is the marginal cost of supplying the next increment of electric energy at a specific bus considering the generation marginal cost and the physical aspects of the transmission system [17]. LMP is the lagrangian multiplier associated with the active power flow equations for each bus in the system [18]. |
| The contribution of this paper is to identify the optimal wheeling transaction where maximum load can be connected in a hybrid power market. The buyer is selected based on their demand side LMP cost and the performance of the system is identified by calculating the power transfer capability. In this paper, OPF is solved using the PSO algorithm for the base case and for the case with identified optimal wheeling transaction. IEEE-30 bus and Indian utility 69 bus systems are used for demonstrating the proposed work. |
II.OVERVIEW OF PARTICLE SWARM OPTIMIZATION (PSO) |
| PSO is a robust stochastic optimization technique based on the movement and intelligence of swarm. This technique was first introduced by Eberhat and Kennedy in 1995. This algorithm simulates the behaviors of bird flocking and fish schooling. The bird which reaches its better solution will inform others, to follow that particular direction in order to get its solution optimally [19]. |
| PSO technique has been successfully applied in many research and application areas. It is validated that, PSO gets better results in a faster way and it has good computational efficiency while comparing with other methods. Here the particles are randomly generated by two parameters (i.e.) position and velocity in the Ndimensional space. Velocity, Vi= (vi1,vi2,…,vin), determines particles searching direct for each iteration. Position of the particle is denoted by, Xi= (xi1,xi2,..,xin). The following equation describes the initialization of each particle’s position and velocity: |
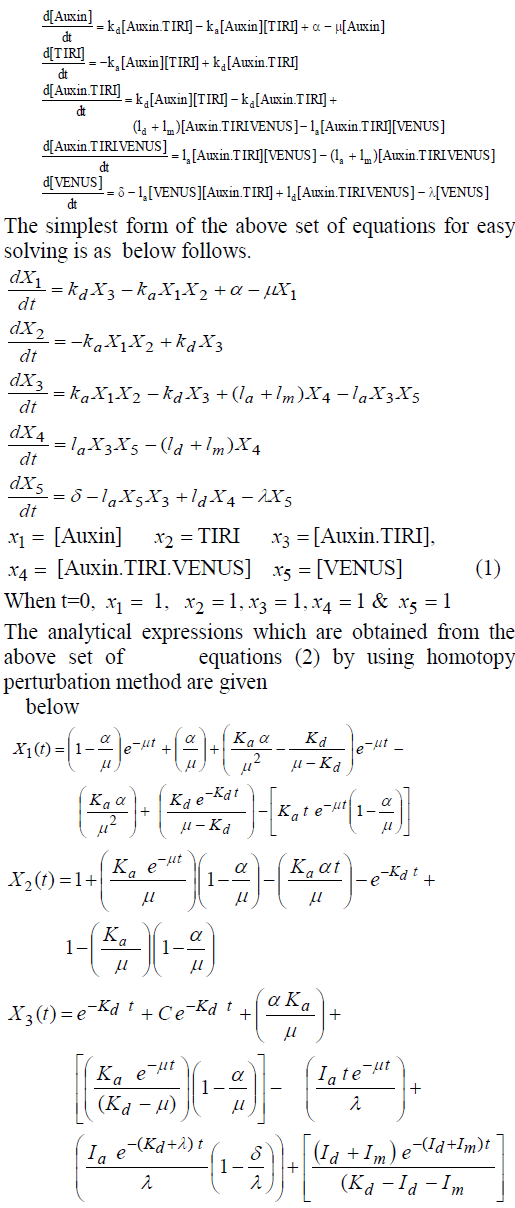 |
| In the velocity updation first part denotes the inertia function part which is important for convergence and it controls the impact of previous history of velocity on the current velocity. w denotes the inertia weight. |
| The second part is the cognitive part which depends on the individual thinking of the particles and the third part is the social part. C1 and C2 are the acceleration constant which pulls the particles towards Pbest and Gbest. |
III.MATHEMATICAL FORMULATION |
| The feasible wheeling transaction can be selected based on the optimization of generation fuel cost by satisfying all the power system constraints. The optimization process can be performed using PSO based OPF. The problem formulation for this approach proceeds as follows: |
A. Objectiv e Function |
| The optimization of generation cost in a power system network is given as |
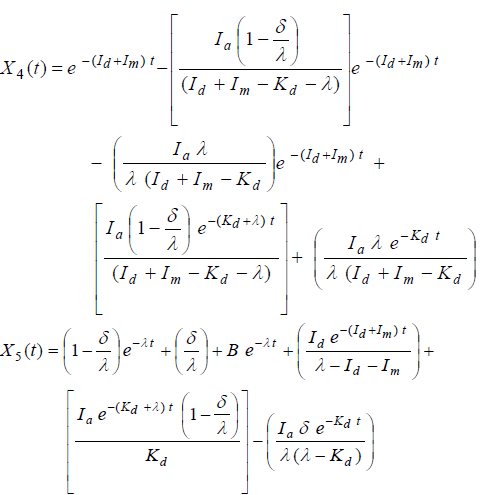 |
1) Equality constraint: |
| The power system network needs to maintain the power balance equation to balance the power transmission. The sum of active power flow injected into a node minus the power flows extracted from the node has to be zero. |
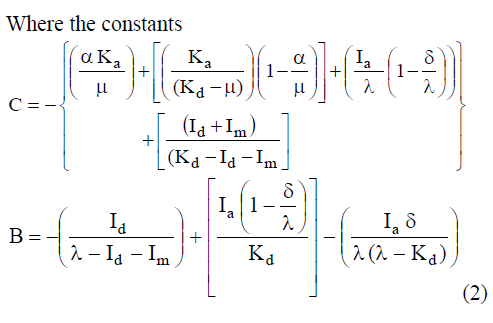 |
B. Locational Mar ginal Price (LMP) |
| The LMP calculates the marginal cost for active power flow in the node. The LMP at a bus is defined as the minimum marginal cost of supplying the next increment of electric energy at the bus without violations of any transmission limits. The prices are determined based on the bids submitted by the power suppliers and consumers in the market. In cases of no congestion the LMP cost is same as Market Clearing Prices (MCP). MCP is determined by the supply and demand curve [17]. |
| The calculation of LMP is based on the marginal cost, supply bid curve, demand curve, physical aspects of the transmission system and the operating constraints of the power system. |
 |
C. Market Model |
| The combined operation of both poolco model and bilateral transaction together is the hybrid model [18]. The ISO is responsible for system operation and guarantees system security in operational matters and holds a superior position. Market participants may not only bid into the pool but also make bilateral contracts with each other. Therefore, this model provides more flexible options for transmission access. |
| A competitive market model is developed by introducing an IPP to the power market. The optimal wheeling transaction is performed in the developed hybrid model. |
IV. ALGORITHM |
| The step by step algorithm for the proposed model is explained as follows, |
| 1. Collect the bus data, line data, real power generation limits and the cost co-efficient of each generating unit. |
| 2. An IPP is connected to the specified location with its total generation capacity. |
| 3. Select the consumer node based on LMP cost. |
| 4. Wheeling transaction is performed with the added IPP and selected buyer. |
| 5. Select the maximum number of iterations, inertia weight, acceleration constants, number of individuals and population size. |
| 6. The maximum allowable load for the selected consumer is identified. |
| 7. OPF based PSO is performed to identify the rescheduled generation unit for optimal wheeling transaction |
IV. RESULTS AND DISCUSSIONS |
A. Test System |
| The proposed method is demonstrated in standard IEEE-30 bus system and Indian utility 69 bus system. The adopted PSO parameters for the proposed technique are given in Table I. |
 |
 |
| The simulation studies have been conducted on Intel(R) core i5, CPU M430 @ 2.27 GHz processor under MatLab 12 environment. |
B. IEEE- 30 Bus System |
| The standard IEEE-30 bus system [20] consists of 6 power suppliers, 24 consumers and 41 transmission lines. The generator sets are connected at nodes 2, 5, 8, 11 and 13 with the slack bus connected to node 1. The system is free from congestion for its base case which is checked by calculating complex power flow in transmission line using Newton-Raphson load flow method. |
| The modified power market with IPP consists of |
| Number of power suppliers = 7 |
| Number of consumers = 23 |
| Number of transmission lines = 41 |
 |
| The LMP is calculated for all the connected consumers neglecting the cost for loss and congestion. The LMP cost for the loads is given in Fig.1. From the Fig.1 bus 7 has been selected as the buyer for wheeling transaction based on LMP calculation. |
 |
 |
| Generator rescheduling is performed using OPF with PSO technique. The maximum allowable load that can be provided for the buyer in bus 7 is identified as 107.2MW in Table III. |
| OPF is performed for 20 different trials for this maximum allowable load and the best solution is selected based on the optimal cost for generator rescheduling. Among the 20 trials performed, the optimal solution is obtained in 8th trial. |
| The rescheduled generation capacity for the trial 8 is given in Table IV |
| The optimal wheeling transaction performed with this rescheduled generation capacity is given in Table V |
 |
| The iteration converges at 251th iteration and the time taken for execution is 1.0591sec. |
C. Indian Utility -69 Bus System |
| The Indian utility 69 bus system [21] consists of 13 power suppliers, 56 consumers and 99 transmission lines. The generator sets are connected at nodes 13, 14, 15, 21, 31, 36, 39, 52, 53, 57, 58 and 60 with the slack bus connected to node 1. The system is free from congestion for its base case which is checked by calculating complex power flow in transmission line using Newton-Raphson load flow method. |
 |
 |
 |
| The modified power market with IPP consists of |
| Number of power suppliers = 14 |
| Number of consumers = 55 |
| Number of transmission lines = 99 |
| The LMP is calculated for all the connected consumers neglecting the cost for loss and congestion. The LMP cost for the loads is given in Fig.2. From the Fig.2 bus 56 has been selected as the buyer for wheeling transaction based on LMP calculation. |
| Generator rescheduling is performed using OPF with PSO technique. The maximum allowable load that can be provided for buyer in bus 56 is identified as 254.3MW in Table VI. |
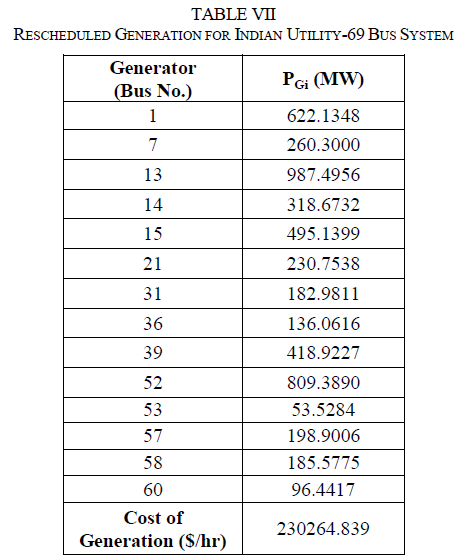
| OPF is performed for 20 different trials for this maximum allowable load and the best solution is selected based on the optimal cost for generator rescheduling. Among the 20 trials performed, the optimal solution is obtained in 2nd trial. The rescheduled generation capacity for the trial 2 is given in Table VII. |
| The optimal wheeling transaction performed with this rescheduled generation capacity is given in Table VIII. |
 |
| The iteration converges at 60th iteration and the time taken for execution is 2.1517sec. The results are obtained for two different systems with the optimal solution for the wheeling transactions |
IV. CONCLUSION |
| The feasible transaction which satisfies all the constraints is identified by rescheduling the generators using PSO. The result proves that the buyer selected based on LMP calculation provides the best location for optimal wheeling transmission. The proposed algorithm works efficiently in standard IEEE-30 bus system and Indian utility 69 bus system. The same can also work efficiently with all the power market. |
ACKNOWLEDGMENT |
| The authors are grateful to the principal and management of K.L.N college of Engineering, Madurai for providing all facilities for the research work. |
References |
|