ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Mr. A. Gopichand1, Ms. R.V.S.Lakshmi2, Mr. B. Maheshkrishna3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Crane hooks are one of the important components which are used to transfer materials having heavy loads, mainly in industries. Crane hooks are liable components subjected to failure due to stress in accumulation of heavy loads. The design parameters for crane hook are area of cross section, material and radius of crane hook. In the present work optimization of design parameters is carried out using Taguchi method, total three parameters are considered with mixed levels and L16 orthogonal array is generated .The optimum combination of input parameters for minimum Vonmises stresses are determined.
Keywords |
| Crane hook; optimization; Taguchi method; |
INTRODUCTION |
| Crane hooks are one of the important components used in industries to carry heavy loads; basically crane hooks are designed with pulley elongated by rope or a chain. In this paper mathematical calculations are done by varying cross sections triangular, trapezoidal, and rectangular with constant area of cross sections for two different materials of steel, cast-iron analysis are evaluated. PRO/E design is prepared, for different cross sections by preparing the trajectory with the parameters taken from the design data book. In this project result of mathematical calculations is compared with the ANSYS with constant area of cross section ,modifying the type of material optimization of better results were done in Taguchi Method. |
LITERATURE SURVEY |
| Travelling cranes of the hand operated type were in use in the 1880’s. About this time complicated designs of powered motion were offered by English and American builders, involving a driving shaft along the runway and multiple clutches for transferring the power of the driving shaft to the hoist, trolley or bridge motions. Study of crane hook for trapezoidal cross section finite element analysis santosh Shaun , in this paper CAE is used to shorten the development FEM concept is used in the locking system of the crane hook stress factor is distributed uniformly[1].Damage factor The database is used to identify the load conditions that were Fatal to those damaged crane-hooks. Some of the feature points are selected on the crane-hook design; the Deformation of a damaged crane-hook can be then obtained based on the feature points detected by means Of the image processing. The critical load condition of the damaged crane-hook is calculated by comparing the obtained actual deformation and the simulated deformation values in the database. On the basis of these calculated load conditions, the critical load condition for the crane-hook is estimated as a statistical Distribution based on the Bayesian approach. Takuma Nishimura, Takao Muromaki, KazuyukiHanahara, Yukio Tada, Shigeyuki Kuroda and Tadahisa Fukui; “Damage Factor Estimation of Crane-Hook [6] |
ANALYTICAL METHOD FOR STRESS CALCULATION |
| Curved beam flexure formula is used when the curvature of the member is pronounced as in cases of hooks and rings for different cross sections mathematical analysis of stress [2] |
 |
TAGUCHI METHOD |
| Taguchi is a technique which is used to predict optimal performance level based on optimal control factor level combination and conduct a confirmation experiment to verify the results product designed with this performance will deliver more consistent performance. Taguchi experimental verification is done based on orthogonal array technique is a systematic software technique is used when no of inputs of the system is relatively small and two large to allow exhaustive testing of every possible input to the system. Table 1 shows the levels of parameters considered for the optimization of design. Using Taguchi design L16 orthogonal array is generated for the mixed levels. |
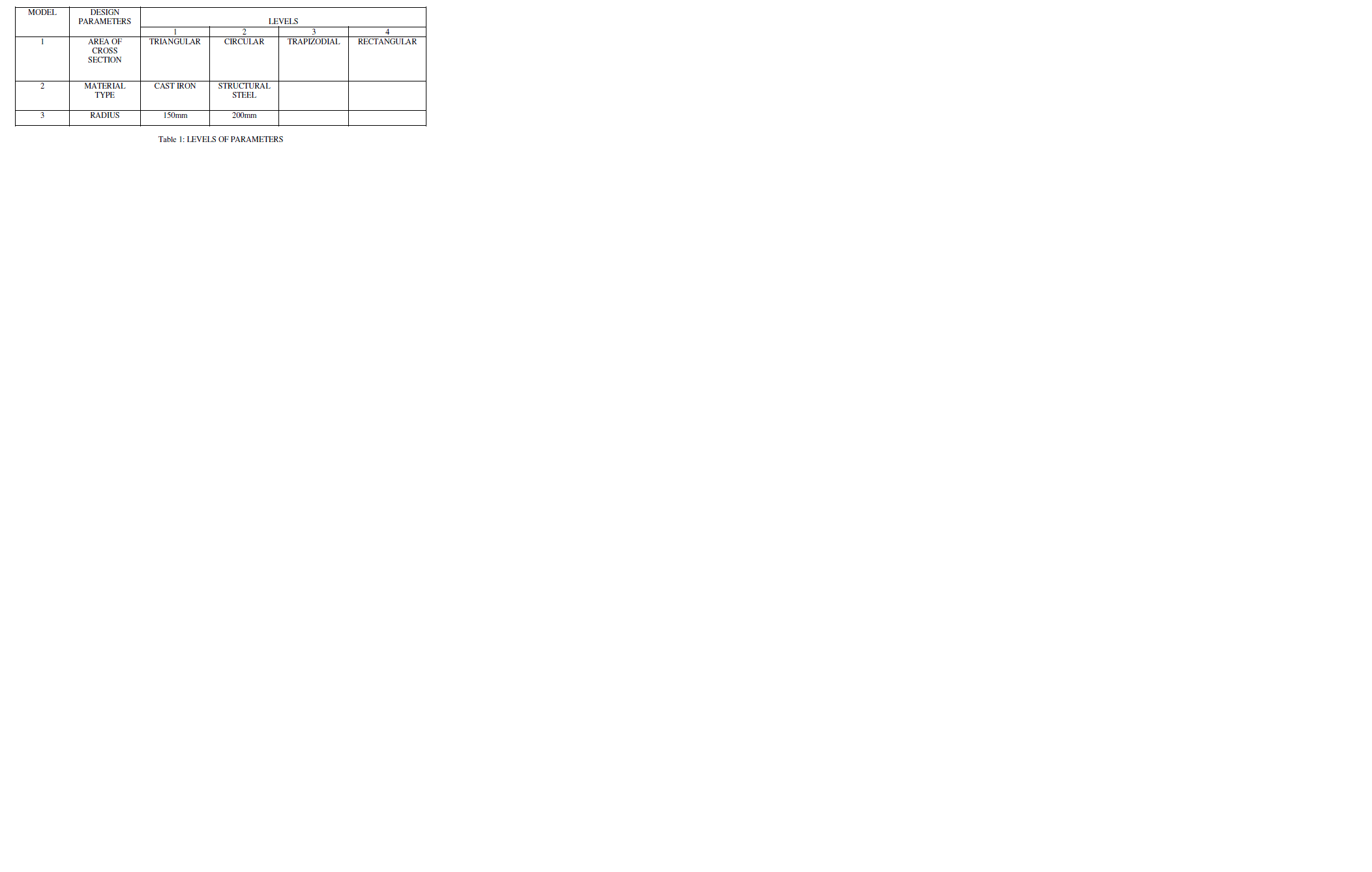 |
| For modelling a crane hook we used the data shown in model-1of orthogonal array L16 as shown in table [2] the required data PRO-E CREO is used to project the trajectory with the required dimensions along with advanced feature of swept blend for the generation of PRO-E .Generated model is saved in the format of i.g.s file similarly for all the cross sections models are generated in PRO-E. |
 |
ANALYSIS USING ANSYS |
| Vonmises Stress Analysis in Ansys: The solid model in i.g.s format is imported to ANSYS WORKBENCH a point load is applied to the model now the simulation process is done for the results. Simulation process meshing of the model is generated as shown in Fig2, for the selection of static analysis fixed support is choosen at shank end and the force is applied in y direction for selected materials of structural steel and cast iron, now the solution is let to solve and Vonmises stresses are detected for different cross sections which are of triangular, circular, rectangular and trapezoidal. For analysing the cross-section of the crane hook after and when it is designed in the PRO-E, loads are applied to check that how much load the designed crane hook with stands. The process of applying load and the results obtained in the Ansys are indicated below |
 |
OPTIMIZATION OF DESIGN PARAMETERS USING TAGUCHI METHOD |
| Based on the orthogonal table mixed level combination with an array of L16 combination is chosen and the parameters of area of cross sections like triangular, circular, trapezoidal, rectangular along with materials of cast iron, structural steel with two different radiuses of 150mm, 200mm. |
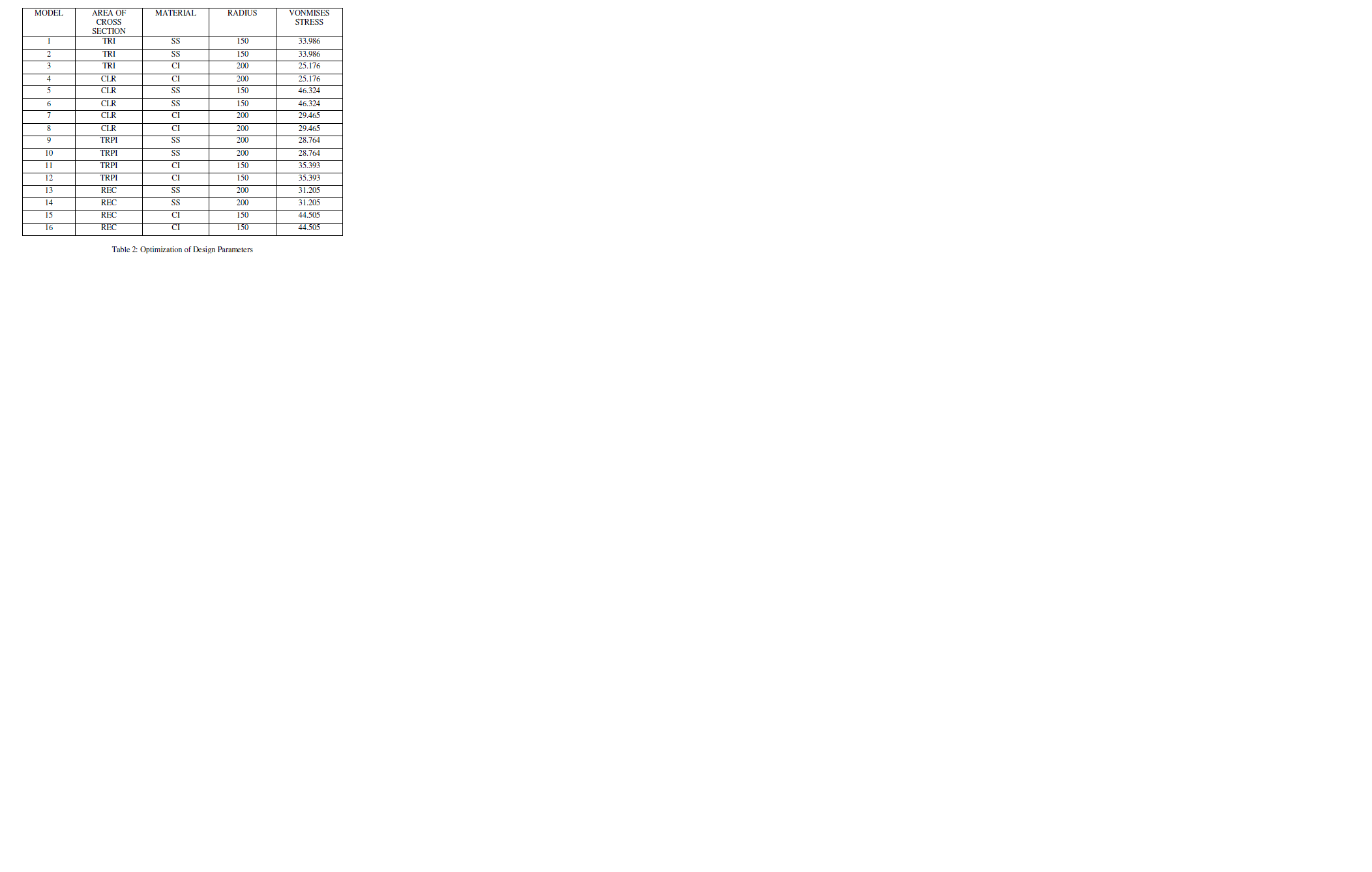 |
RESULTS AND DISCUSSIONS |
| Taguchi analysis is performed on the L16 orthogonal array for minimizing Von mises stress considering the option smaller is better .From the main effects plots from SN ratio the optimum combination of input parameters are determined by considering the maximum points in the plot for various parameters, triangular cross section cast-iron as material with radius 200mm . |
 |
| Using the table[2] the Vonmises stress for the above mentioned combination is 25.176 MPa which is minimum value. |
CONCLUSION |
| From the Taguchi analysis the optimum combination of input parameters for von misses stress were determined using SN ration plots, The optimum combination is TRIANGULAR cross section ,CASTIRON material and 200mmRADIUS .The first model simulation values are compared with analytical values and the error is 9.26%which is acceptable. |
References |
|