ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Priyanka Tamgave, Shobhika Jain, Gitanjalee Waghmode, Shweta Udagire1 , Jayant Umale2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Travelling tournament problem(TTP) is evolved NP-hard problem from its similarity to Travelling Salesman problem.(TSP). TTP aims to solve optimization of objectives to stimulate the schedule of tournaments which now a days is used in such organizations. The availability of resources, constraints and objectives for optimization makes TTP problem hard to produce successful results efficiently. The optimization approaches used to solve complex TTP problem with higher number of teams and venues by researchers shows the partially accurate results with higher execution time. We propose here the novel approach to solve TTP using Genetic algorithm (GA) which tend to produce accurate results compared to existing approaches. We further extend this solution to reduce execution overhead of GA using parallel decomposition of GA. In this paper we present the proposed project work to optimize TTP using hierarchical parallel GA (HPGA) implementation on Hadoop Map Reduce
Keywords |
| Genetic Algorithm, Map Reduce , Hadoop , TTP , HPGA. |
INTRODUCTION |
| Optimization is the process of making something better. An optimization problem is the problem of finding the best solution from all available solution spaces. The terminology “best” solution implies that there is more than one solution. Optimization is finding maxima or minima of a solution space. The Traveling Tournament Problem (TTP) is combinatorial problem that combines features from Traveling Salesman Problem (TSP) and Tournament Scheduling Problem. TTP represents the fundamental issues involved in creating schedule for sports league where the distance travelled by teams is an important issue. With the available constraints and objectives, TTP is known as NP-Hard problem. Research work in this area shows the efforts to obtain solution for TTP by using classical methods such as Greedy, dynamic programming and Backtracking. Also research shows that use of evolutionary methods such as Genetic Algorithms (GAs), Simulated Annealing (SA), Ant Colony Optimization (ACO) and Tabu Search (TS) have proved to be suitable candidates to obtain effective solutions. Research in this direction shows the use of Genetic algorithm (GA) as promising candidate and is preferred over other optimization methods. GA has ability to find accurate solution from solution space because it has ability to consider random jumps in solution space, since mutation gives this ability to GA to evaluate solution space. GA finds best or accurate solution with large number of iterations and becomes slower for immediate requirements of execution time. GA can be easily parallelized to increase its computing ability because of its inherent parallelism, and hence offers great potential towards solving hard problems. Map Reduce paradigm evolved by Google and readily available from the open source platforms like Hadoop suits to efficient parallelization of algorithm. The Map Reduce model provides a parallel design pattern for simplifying application developments in distributed environments. Map Reduce can split a large problem space into small pieces and parallelize the execution using small tasks on the smaller space. The Hadoop Provides open source implementation of Map Reduce Framework. As we are using GA with large population, the support of Map Reduce and Hadoop Distributed files system (HDFS) helps to stimulate parallelization of GA. The paper covers the notes on TTP, GA and Map Reduce and their use to stimulate the solution for TTP using parallel GA. |
Travelling Tournament Problem (TTP) : |
| Travelling Tournament Problem is a sports timetabling problem that abstracts the important issues in creating timetables where team travel is an important issue. Professional sports leagues exist all over the world. Popular leagues are often of huge economic importance due to the enormous revenues generated by selling tickets and broadcasting rights for the games. Hence, the planning of these leagues is of major importance. An important aspect is the generation of a timetable for the tournaments that specifies the order in which the teams play with each other during the season and the venue of each game. Given the number of teams and the pair-wise distances between their home venues, TTP asks for a timetable of a double round robin tournament that minimizes the sum of the distances travelled by the teams during the season. The Travelling Tournament Problem (TTP) is a tournament scheduling problem with a strong optimisation component . Problem is stated as , “ Given n teams with n even, a double round robin tournament is a set of games in which every team plays with every other team exactly once at home and once away. A game is specified by an ordered pair of opponents. Exactly 2(n-1) slots or time periods are required to play a double round robin tournamen. Distances between team sites are given by an nXn distance matrix D”. Each team begins at its home site and travels to play games at the chosen venues. Each team then returns (if necessary) to its home base at the end of the schedule. Hence, the problem is to optimize (minimize) the cost of average travelling by deciding the optimized scheduled . Input: N, the number of teams |
| D, an nXn distance matrix; Output: The final tournament schedule which satisfies all the constraints and has minimum total distance travelled by the teams . |
| Problem Formulation: |
| ïÃâ÷ N (even) teams take part in a tournament |
| ïÃâ÷ Each team has its own stadium at its home city |
| ïÃâ÷ Distances between the stadiums are known |
| Constraints: |
| Each team say, A and B, play exactly twice: once at A’s home ground (B@A) and once at B’s home ground (A@B). Thus there are 2(n-1) rounds and in each round n/2 games are played (Double Round-robin Constraint) |
| For any team say, A and B, A@B cannot follow B@A immediately in the next round (No repeater constraint) |
Genetic Algorithm: |
| Genetic Algorithm (GA) is adaptive heuristic search algorithm based on the idea of natural evolution. Genetic algorithm belongs to the larger class of evolutionary algorithms (EA), which generates solutions to optimization problems using techniques inspired by natural evolution, such as inheritance, mutation, selection, and crossover. In nature, "survival of the fittest" will make the adapted species to be selected and produce subsequent generations. It is expected that the average fitness or adaptation of each generation improves over that of the current generation, because each generation inherits good features from the current generation. Conceptually, this means that we will achieve a population composed of identical individuals. However, mutation occurs and introduces diversification in the population and prevents this homogeneous situation. |
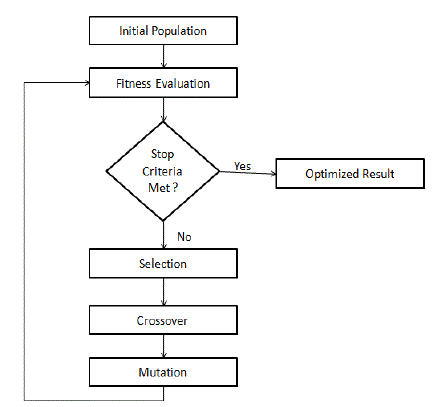 |
Fig. 1: GA flowchart |
| Mapping GA Logic to our implementation follows that the initial population will be the random set of schedules satisfying the constraints. This population will be then equally divided among the nodes available by the server. The process of crossover , mutation and fitness function will be executed on each of these nodes. Results from each nodes will be gathered and the best solution will be determined. The solution thus obtained from the current generation will be compared with the solution of the previous generation and the most feasible solution will be considered. This process will continue until the specified number of generations. |
Map Reduce and Hadoop: |
| MapReduce is a programming model for processing large data sets with a parallel, distributed algorithm on a cluster. A MapReduce program is composed of a Map() procedure that performs filtering and sorting and a Reduce() procedure that performs a summary operation . In MapReduce we can split a large problem space into small pieces and parallelize the execution using small tasks on the smaller space. This was proposed by Google for easily harnessing a large number of resources in data centers to process data-intensive applications. |
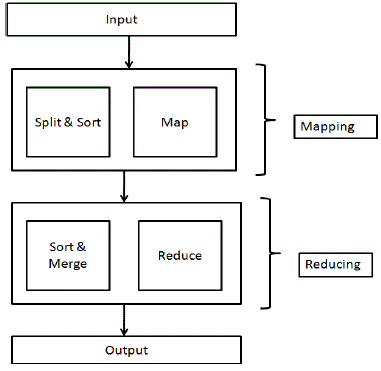 |
Fig 2: MapReduce Framework |
| Hadoop is the most popular open-source implementation of the MapReduce framework. Hadoop is a free, Java-based programming framework that supports the processing of large data sets in a distributed computing environment. It is part of the Apache project sponsored by the Apache Software Foundation. The current Apache Hadoop ecosystem consists of the Hadoop kernel, MapReduce, the Hadoop distributed file system (HDFS) and a number of related projects such as Apache Hive, HBase and Zookeeper. Its distributed file system facilitates rapid data transfer rates among nodes and allows the system to continue operating uninterrupted in case of a node failure. This approach lowers the risk of catastrophic system failure, even if a significant number of nodes become inoperative. |
II. RELATED WORK |
| The travelling tournament problem (TTP) was introduced by Easton , Nemhauser and Trick [3] .In this ,they had combined integer and constraint programming methods to solve larger problems much more quickly. Constraint programming has been successfully used to solve complex timetabling feasibility problems [8] while integer programming has been successfully used to solve difficult optimality problems like the TSP [1].However ,integer programming or Constraint Programming so far has been possible only for instances up to eight teams. Tabu search [5] is an iterative search procedure and local search algorithm, where solutions are examined once at a time: the next solution is generated by making some changes to current solution in some small way. By applying certain rules at each step, these methods guide the search toward a solution which best satisfies some criteria, i.e. a solution with a sufficiently low (or high) objective function value. Anagnostopoulos ,Van and Vergados [6] had proposed a simulated annealing approach to the TTP.The gradual 'cooling' process makes the simulated annealing algorithm remarkably effective at finding a close to optimum solution when dealing with large problems which contain numerous local optimums.SA can find good quality solutions in a neighbourhood, however , most likely it will get trapped in local minima and takes longer to escape. Crauwels and Van Oudhesusden [4] developed an ant colony optimisation algorithm that can compete with some of the best mathematical techniques. Pai-Chun Chen, Kendal and Berghe [8] had developed an ant based hyperheuristics solution for TTP. It has been successfully applied to solve combinatorial optimization problems, but it has some drawbacks such as stagnation behaviour, long computational time, and premature convergence. The novelty of this approach is that we can tackle all problem instances using the same algorithm, and using the same parameters. Genetic Algorithms[2] follows a similar rule for sticking to what is known to be good when searching for improved solutions. Here, the notation is that GA rests on the premise that a good solution contains several good subparts. Therefore genetic algorithm builds on what is already know to be a good by taking parts of two solutions and merging them to create new solution. As the GA executes sequentially by steps[1], the time required to compute is also higher. Number of objectives to be satisfied is the yet another factor that further delays the execution. Another issue with sequential implementation is its memory utilization for storing large population. The run time memory requirements are also higher since the population. |
III. PROPOSED WORK |
| As the Project work we proposed the framework for GA call Hierarchical parallel GA(HPGA). The proposed variants GA consists of decomposing the population into smaller cluster and operating GA on this cluster.The HPGA aims of generating the population from multiple instances of GA executing on cluster. The best fit solution generate at GA instance gets added to overall population at server central population database. And also how these HGAs can be applied to optimization problem like Travelling Tournament Problem (TTP) ,using Map Reduce , which is a software framework that is used to support distributed computing on large data sets on a clusters of computers. So in the following section we present an architecture showing how this problem can be solved on this framework in a hierarchical way. Proposed Architecture We propose to decompose GA using both task and data (population) strategies. The structure for decomposition will be hierarchical |
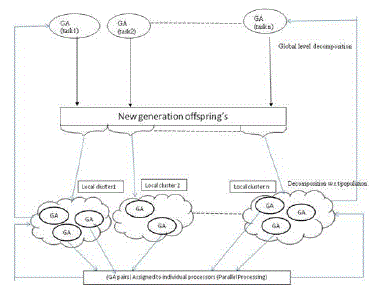 |
Fig 3 : Hierarchical Parallel Genetic Algorithm |
| The global level of decomposition will work by decomposition of multiple GA tasks which are assigned to local decomposition level. The local level will be responsible to decompose the offered population and run parallel tasks on the local infrastructure- computing clusterThe diagram shows the local and global level decomposition of GA. We propose to use Map Reduce model of programming. The Map Reduce model provides a parallel design pattern for simplifying application developments in distributed environments. In MapReduce we can split a large problem space into small pieces and parallelize the execution using small tasks on the smaller space. This was proposed by Google for easily harnessing a large number of resources in data centers to process data-intensive applications. Hadoop allows users to delegate tasks to the middleware and distribute as per given strategy. This happens more transparently as hadoop supports this by the implementation of low level communication interfaces for cluster. |
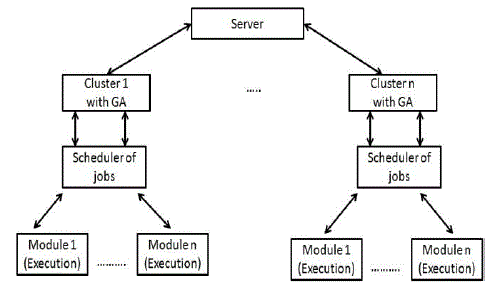 |
Fig 4: Architecture |
| Algorithm |
| We propose the following algorithm for the above mentioned architecture. |
| 1. Accept input from the user. |
| 2. Generate at random a population (schedules), P, of chromosomes i.e. the solution space. |
| 3. Divide the population P among the available clusters (done by server machine). |
| 4. on individual cluster: |
| 4.1 Accept the population (P) and the objective (O). |
| 4.2 Divide accepted population among the nodes in individual cluster |
| 4.3 On individual node |
| 4.3.1Execute local GA |
| 4.3.2 Apply the selection mechanism and the genetic operators using MapReduce. |
| 4.3.3 If the stop criteria not fulfilled, return to 4.3.1 |
| 4.4 Combine the results from the all the nodes |
| 4.5 Send the best results to the top i.e. server machine. |
| 5. Gathering of best results from all clusters on server machine. |
| 6. Execute the fitness function on server to get the best results. |
| 7. Display the Best or optimized final results. |
Flowchart: |
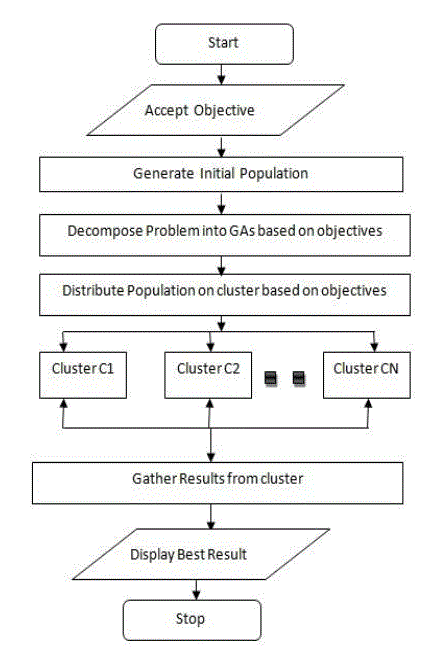 |
Fig 5: Operation on server side1 |
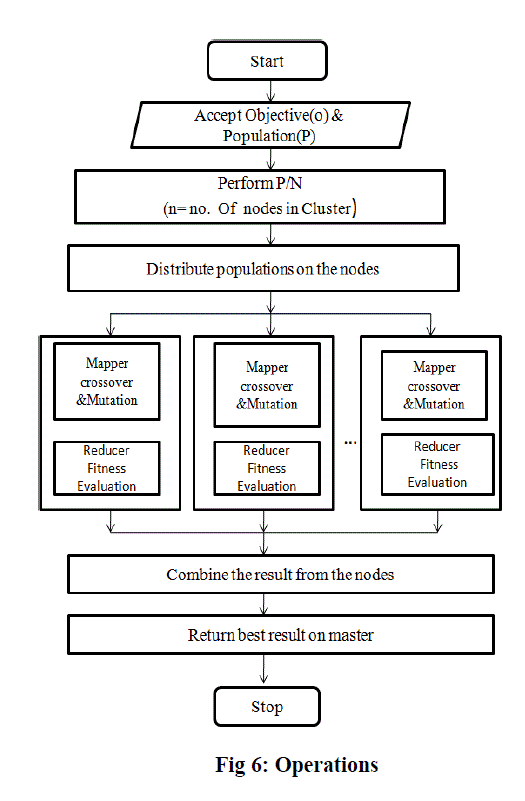 |
IV. CONCLUSION AND FUTURE WORK |
| This paper proposes the optimization of GA for TTP problem. We conclude that the implementation of the HPGA on Map Reduce as proposed will reduce execution time and provide accurate solution. The execution of GA in hierarchical steps HPGA shown here will produce solutions efficiently necause of independent GA tasks. The partitioning of population would increase the scope to consider large population with independent executions. As future work, the implementation can be extended to multiobjective GA with Map Reduce. Also simillar implementations can also be compared on CUDA and MPI. |
References |
|