ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| R.Pandithurai, I. Ambrose Edward Velammal college of Engineering and Technology, Madurai, TamilNadu, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Wire Electro Discharge machining (WEDM) is one of the important non-traditional machining processes which are used for machining difficult to machine materials like composites and inter-metallic materials. Intricate profiles used in prosthetics, bio-medical applications can also be done in WEDM. WEDM involves complex physical and chemical process including heating and cooling. The electrical discharge energy affected by the spark plasma intensity and the discharging time will determine the crater size, which in turn will influence the machining efficiency and surface quality. This paper presents an effective approach to optimize process parameters for Wire electro discharge machining (WEDM).WEDM is extensively used in tool and die industries. Precision and intricate machining are the strengths. While machining time and surface quality still remains as major challenges. The main objective of this study is to obtain higher material removal rate (MRR) and lower surface roughness (SR). Ton, T off, Gap voltage and wire feed rate are the four control factors taken each at various levels. The genetic algorithm optimization tool is used to find the factors level that create a low surface roughness in WEDM.
Keywords |
| Genetic algorithm, Optimization, Process parameters, Surface roughness, Wire-EDM |
INTRODUCTION |
| Electric discharge machining (EDM), sometimes colloquially also referred to as spark machining, spark eroding, burning, die sinking or wire erosion, is a manufacturing process whereby a desired shape is obtained using electrical discharges (sparks). |
| Material is removed from the work piece by a series of rapidly recurring current discharges between two electrodes, separated by a dielectric liquid and subject to an electric voltage. One of the electrodes is called the toolelectrode, or simply the âÃâ¬Ãâtool‘ or âÃâ¬Ãâelectrode‘, while the other is called the work piece-electrode, or âÃâ¬Ãâwork piece‘. |
| When the distance between the two electrodes is reduced, the intensity of the electric field in the volume between the electrodes becomes greater than the strength of the dielectric (at least in some point(s)), which breaks, allowing current to flow between the two electrodes. This phenomenon is the same as the breakdown of a capacitor (condenser) (see also breakdown voltage). As a result, material is removed from both the electrodes |
 |
A. Generalities |
| Electrical discharge machining is a machining method primarily used for hard metals or those that would be very difficult to machine with traditional techniques. EDM typically works with materials that are electrically conductive, although methods for machining insulating ceramics with EDM have also been proposed. EDM can cut intricate contours or cavities in pre-hardened steel without the need for heat treatment to soften and re-harden them. This method can be used with any other metal or metal alloy such as titanium, hastelloy, kovar, andinconel. Also, applications of this process to shape polycrystalline diamond tools have been reported. |
| EDM is often included in the âÃâ¬Ãânon-traditional‘ or âÃâ¬Ãânon-conventional‘ group of machining methods together with processes such as electrochemical machining (ECM), water jet cutting (WJ, AWJ), laser cutting and opposite to the âÃâ¬Ãâconventional‘ group (turning, milling, grinding, drilling and any other process whose material removal mechanism is essentially based on mechanical forces). |
| The inter-electrode distance, often also referred to as spark-gap, is the end result of the control algorithms of the specific machine used. The control of such a distance appears logically to be central to this process. |
B. Types |
1) Sinker EDM . |
| Sinker EDM allowed quick production of 614 uniform injectors for the J-2 rocket engine, six of which were needed for each trip to the moon. Sinker EDM, also called cavity type EDM or volume EDM consists of an electrode and work piece submerged in an insulating liquid such as, more typically, oil or, less frequently, other dielectric fluids |
| These sparks usually strike one at a time because it is very unlikely that different locations in the inter-electrode space have the identical local electrical characteristics which would enable a spark to occur simultaneously in all such locations. |
2) Wire EDM |
| In wire electrical discharge machining (WEDM), also known as wire-cut EDM and wire cutting, a thin singlestrand metal wire, usually brass, is fed through the work piece, submerged in a tank of dielectric fluid, typically deionized water. Wire-cut EDM is typically used to cut plates as thick as 300mm and to make punches, tools, and dies from hard metals that are difficult to machine with other methods. |
| The wire, which is constantly fed from a spool, is held between upper and lower diamond guides. The guides, usually CNC-controlled, move in the x–y plane. On most machines, the upper guide can also move independently in the z–u–v axis, giving rise to the ability to cut tapered and transitioning shapes (circle on the bottom square at the top for example). The upper guide can control axis movements in x–y–u–v–i–j–k–l–. This allows the wire-cut EDM to be programmed to cut very intricate and delicate shapes. |
| The upper and lower diamond guides are usually accurate to 0.004 mm, and can have a cutting path or kerf as small as 0.12 mm using Ø 0.1 mm wire, though the average cutting kerf that achieves the best economic cost and machining time is 0.335 mm using Ø 0.25 brass wire. The reason that the cutting width is greater than the width of the wire is because sparking occurs from the sides of the wire to the work piece, causing erosion. |
| This "over cut" is necessary, for many applications it is adequately predictable and therefore can be compensated for (for instance in micro-EDM this is not often the case). Spools of wire are long—an 8 kg spool of 0.25 mm wire is just over 19 kilometers in length. Wire diameter can be as small as 20 micrometers and the geometry precision is not far from +/- 1 micrometer. |
II. PROBLEM IDENTIFICATION |
| The formulation of an optimization problem begins with identifying the underlying design variables, which are primarily varied during the optimization process. In this paper machining speed, pulse on time, pulse off time and peak current are considered as design. |
| The mathematical models are obtained for mild steel specimens. Evidence shows that the mathematical models derived by the Genetic Algorithm are sufficiently precise to present the real machining performance. The objective functions for metal removal rate are obtained based on the mathematical models. The cutting parameters considered for optimization in this work are given below |
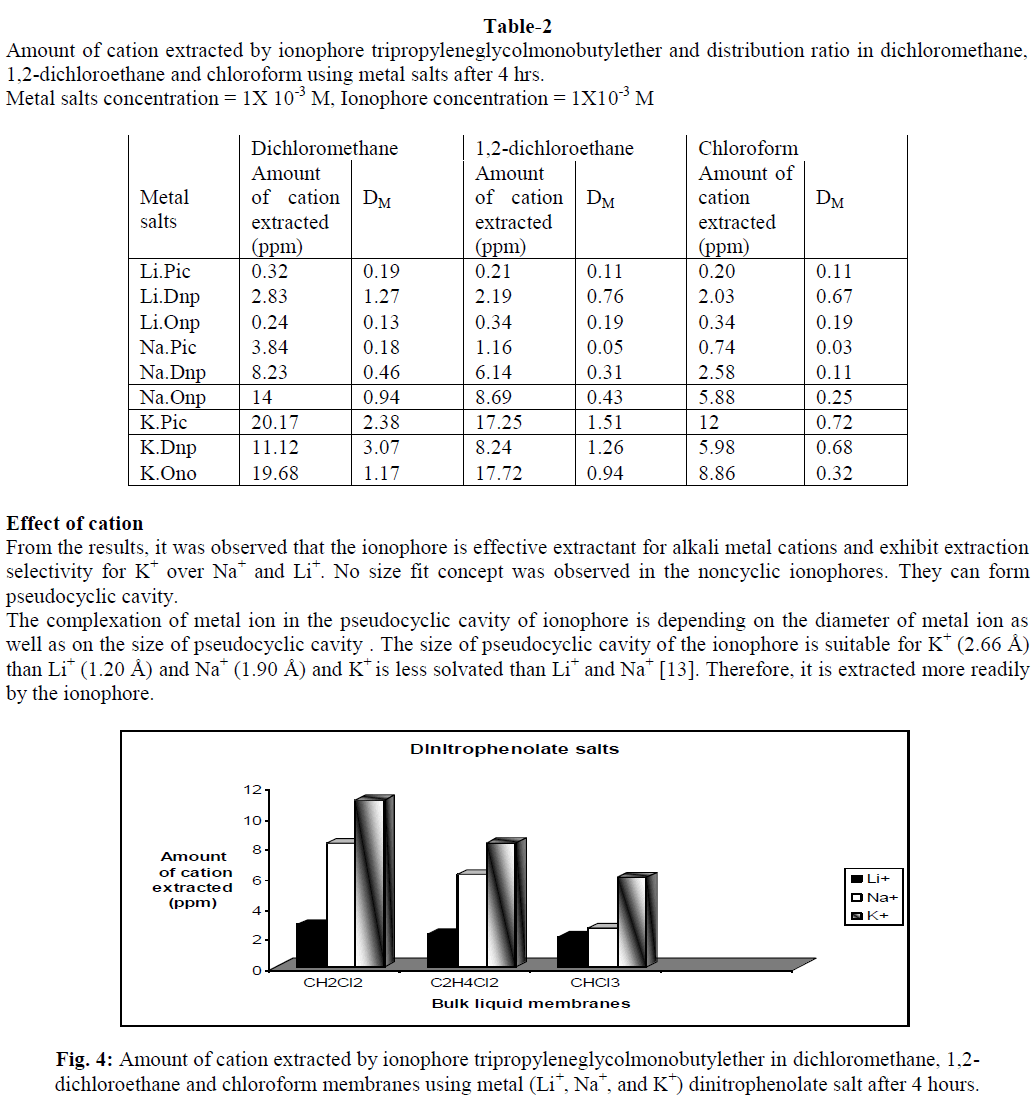
| • Discharge current (Ip) |
| • Pulse on time (Ton) |
| • Pulse off time (Toff) |
| • Peak current |
| • Gap voltage |
| • Wire feed rate |
| The objective of this model is to maximize the surface roughness. The formula for calculating the above surface roughness is as given by, |
 |
III. METHODOLOGY |
A. Genetic Algorithm |
| A genetic algorithm (GA) is a search heuristic that mimics the process of natural evolution. This heuristic is routinely used to generate useful solutions to optimization and search problems. Genetic algorithms belong to the larger class of evolutionary algorithms (EA), which generate solutions to optimization problems using techniques inspired by natural evolution, such as inheritance, mutation, selection, and crossover. |
| Genetic algorithms find application in bioinformatics, phylogenetics, computational science, engineering, economics, chemistry, manufacturing, mathematics, physics and other fields. |
B. Fundamental theorem of genetic algorithms |
| A chromosome is a long, complicated thread of DNA (deoxyribonucleic acid). Hereditary factors that determine particular traits of an individual are strung along the length of these chromosomes, like beads on a necklace. Each trait is coded by some combination of DNA (there are four bases, A (Adenine), C (Cytosine), T (Thymine) and G (Guanine). Like an alphabet in a language, meaningful combinations of the bases produce specific instructions to the cell. |
| Changes occur during reproduction. The chromosomes from the parents exchange randomly by a process called crossover. Therefore, the offspring exhibit some traits of the father and some traits of the mother. A rarer process called mutation also changes some traits. Sometimes an error may occur during copying of chromosomes (mitosis). The parent cell may have -A-C-GC- T- but an accident may occur and changes the new cell to -A-C-T-C-T-. Much like a typist copying a book, sometimes a few mistakes are made. Usually this results in a nonsensical word and the cell does not survive. |
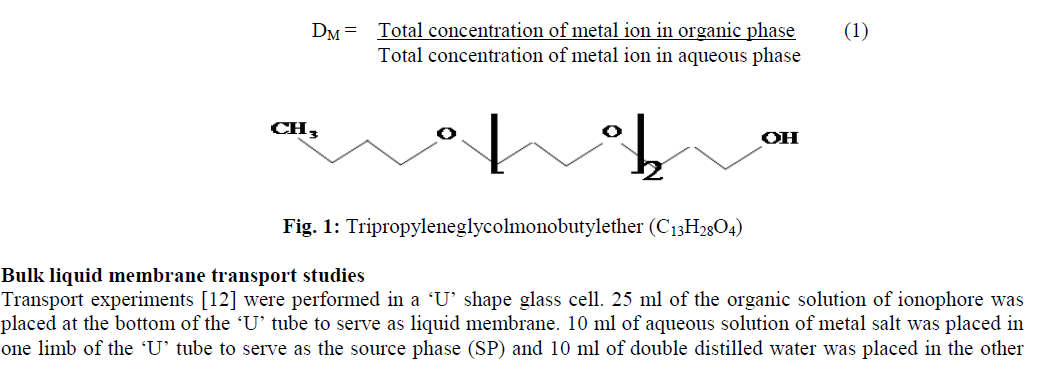
| genetic algorithm is constructed by stochastic operators, and its robust search ability is based on the theorem depicted in, which states, "short schemata of low order with aptitude above average, and exponentially increase its number by generations ", this is: |
| where m(H,t+1) and m(H,t) are the schemata number H in the generation t+1 and t respectively, f(H) is the average aptitude value of the strings that is included on the schemata H, favg is the total population's average aptitude value, l is the total string length, d(H) is the schemata length from H, O(H) is the schemata order from H, pc is the crossover probability and pm is the mutation probability. |
C. Genetic Algorithm Operators |
| As shown above, a basic genetic algorithm that can produce acceptable results in many practical problems is composed of three operators: |
| • Reproduction |
| • Crossover |
| • Mutation |
1) Reproduction |
| The reproduction process goal is to allow the genetic information, stored in the good fitness artificial strings, survive the next generation. The typical case is where the population's string has assigned a value according to its aptitude in the object function. This value has the probability of being chosen as the parent in the reproduction process of a new generation. |
2) Crossover |
| The crossover is a process by which a string is divided into segments, which are exchanged with the segments corresponding to another string. With these process two new strings different to those that produced they are generated. |
| It is necessary to clarify that the choice of strings crossed inside those that were chosen previously in the reproduction process is random. From the point of view of problem optimization, it is equal to the exploitation of an area of the parameters space. |
3) Mutation |
| As with biological systems the mutation is manifested with a small change in the genetic string of the individuals. In the case of artificial genetic strings, the mutation is equal to a change in the elementary portion (allele) of the individuals‘ code. The mutation takes place with characteristics different to those that the individuals had at the beginning, characteristics that didn't possibly exist in the population. |
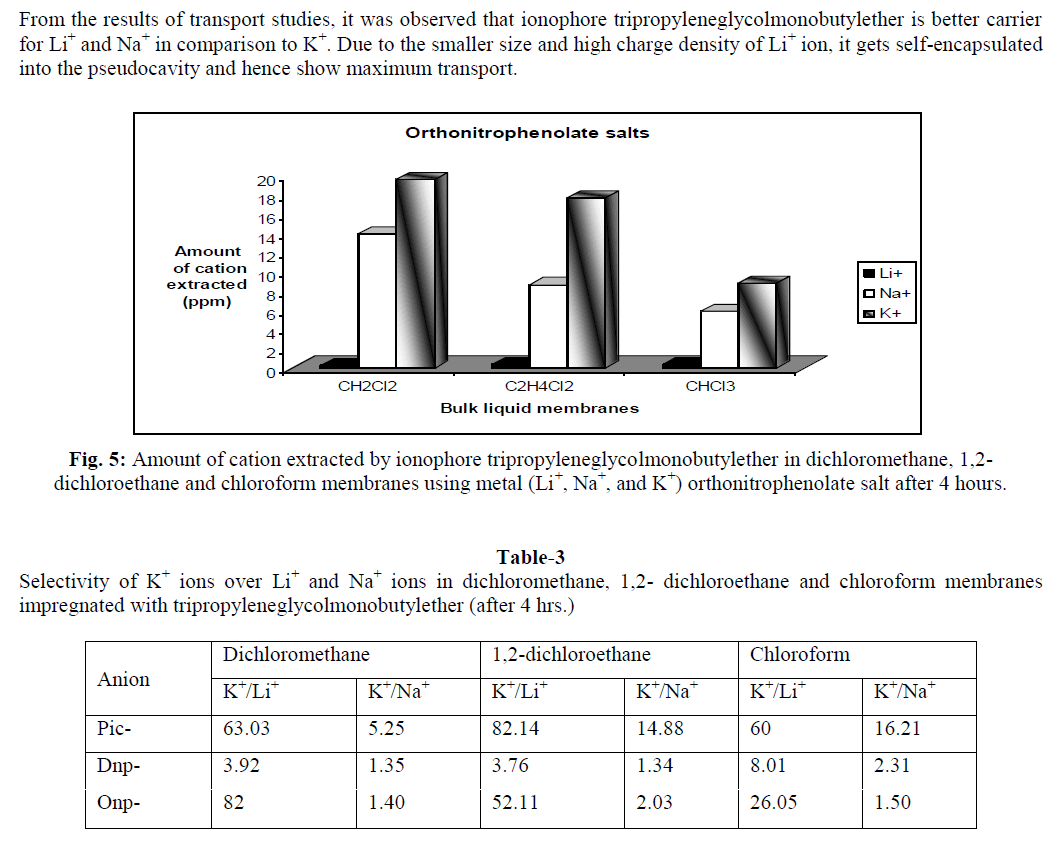 |
4) Steps in the Genetic Algorithm Method |
| Step 1: Initialization randomly generate an initial population of chromosomes and evaluate the fitness function to a function to be maximized for the encoded version) for each of the chromosomes. |
| Step 2: Parent Selection Set if elitism strategy is not used; otherwise. Select with replacement parents from the full population (including the elitist elements). The parents are selected according to their fitness, with those chromosomes having higher fitness value being selected more often. |
| Step 3: Crossover For each pair of parents identified in Step 1, perform crossover on the parents at a randomly (perhaps uniformly) chosen splice point (or points if using multi-point crossover) with probability. If no crossover takes place (probability), then form two offspring that are exact copies (clones) of the two parents. |
| Step 4: Replacement and Mutation While retaining the best chromosomes from the previous generation, replace the remaining chromosomes with the current population of offspring from Step 2. For the bit-based implementations, mutate the individual bits with probability ; for real coded implementations, use an alternative form of ''small'' modification (in either case, one has the option of choosing whether to make the elitist chromosomes candidates for mutation). |
| Step 5: Fitness and End Test Compute the fitness values for the new population of chromosomes. Terminate the algorithm if the stopping criterion is met or if the budget of fitness function evaluations is exhausted; else return to Step1. |
| Before crossover |
| 00011110110001110 1100010111011 |
| 01101010110011101 0100001000100 |
| After crossover |
| 000111101100011100100001000100 |
| 011010101100111011100010111011 |
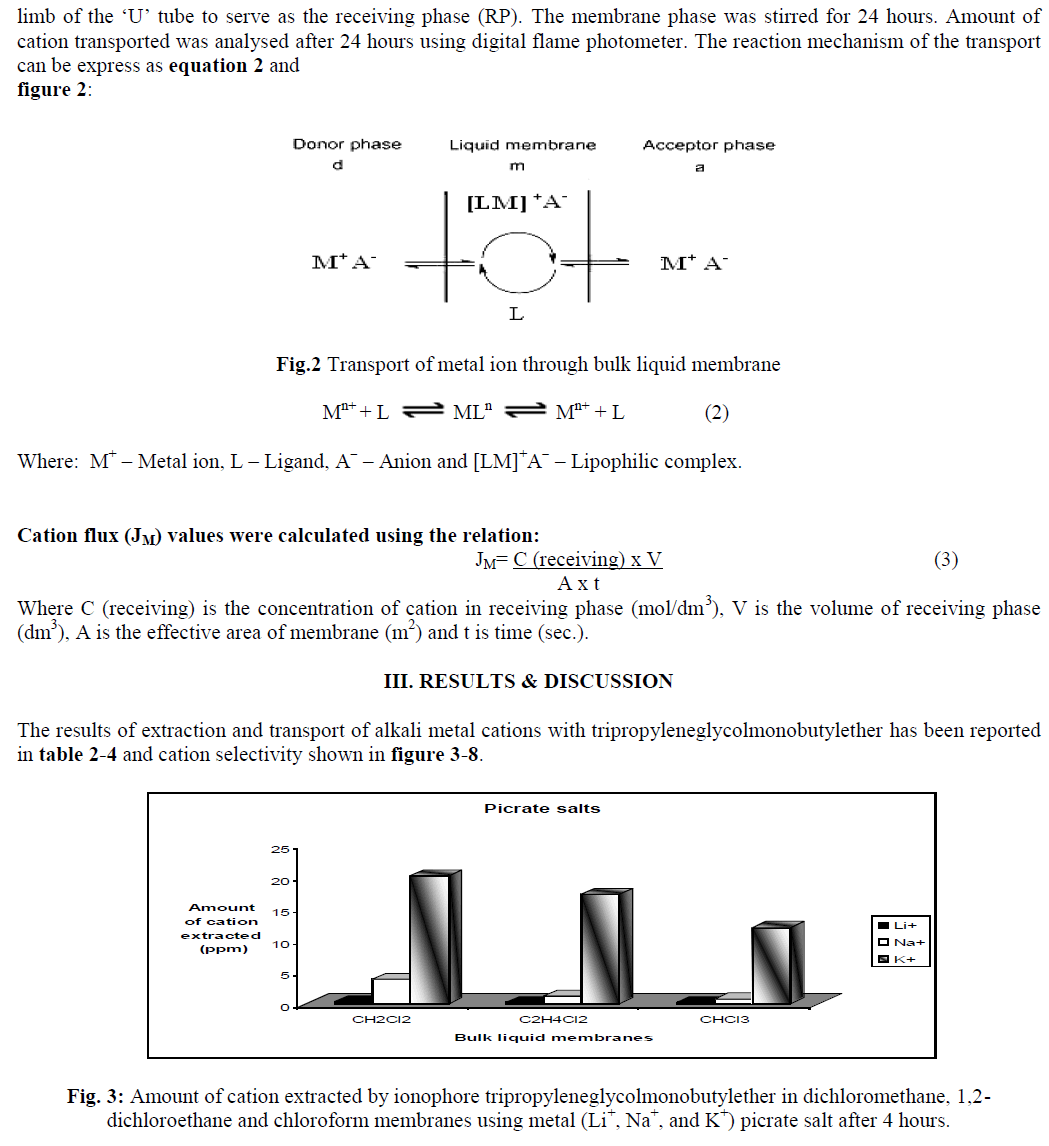
6) Fitness Function |
| 1. Genetic Algorithm mimics the survival of the fittest principle of nature to make search procedure |
| 2. The fitness function F (x) is first derived from the objective function and used in successive genetic operation. |
| 3. For minimization problems, the fitness function is an equivalent maximization problem such that the optimum point remains unchanged. |
 |
| Genetic Algorithm [4, 6, and 7] begins with population of random strings representing design and decision variables thereafter each string is evaluated to find the fitness value. |
 |
  |
IV.CONCLUSIONS |
| GA‘s are derivative-free calculations and therefore, are neither bound to assumptions regarding continuity, nor limited by required prerequisites. As Goldberg stated, GAs are blind. They can handle any kind of objective function and any kind of constraints (e.g., linear or nonlinear) defined on discrete, continuous or mixed search spaces. In addition, as stated earlier, they are robust in producing near-optimal solutions, with a high degree of probability to obtain the global Optimum. A genetic algorithm was proposed for optimizing the machining parameters. The main advantage of this approach is that it can be used for any objective function, which was most clearly demonstrated in this example, where the objective function was the minimization of surface roughness. |
References |
|