International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Optimum Design of Disc Brake Using NSGAII Algorithm

P.Sabarinath1, R.Hariharasudhan1, M.R.Thansekhar1 R.Saravanan2
  1. Department of Mechanical Engineering, KLN College of Engineering, Madurai, Tamilnadu, India1,
  2. Department of Mechanical Engineering, Sri Krishna College of Technology, Coimbatore, Tamilnadu4
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

This work presents an application of improved Elitist Non-dominated Sorting Genetic Algorithm version II (NSGAII), to multi-objective disc brake optimization problem. The disc brake optimization problem is considered as a two-objective problem. The first objective is the minimization of the mass of the brake and the second objective is the minimization of the stopping time. The disc brake optimization model has four design variables and five inequality constraints. To improve the performance of NSGA-II, two modifications are proposed. One modification is incorporation of Virtual Mapping Procedure (VMP), and the other is introduction of controlled elitism in NSGA-II. The main objective of this project is to apply NSGA-II Algorithm for optimizing the design of Disc Brake for minimization of brake mass and stopping time and to compare the results obtained by NSGA-II Algorithm with that of the results already published for Genetic Algorithm.

Keywords
Combinatorial optimization, Disc brake, Multi-objective, Non-dominated Sorting Genetic Algorithm (NSGA-II)

INTRODUCTION
The present scenario in industries is to design and manufacture high quality products that not only satisfies the customer demands but also meets the heavy competition in the market. The current design and manufacturing techniques available in the industry must be improved in order to meet the challenges and to become winners of the competitive market. The design and manufacturing companies have been forced to make radical changes in design and manufacturing strategies in recent years so as to face the fierce competition conditions in the market. The crucial task nowadays is to find the optimal design and machining parameters so as to minimize the production costs. The optimal design problems consist of the selection of optimal design variables. Even though these problems have been extensively researched, the complexity of optimal design of machine elements creates the requirement for increasingly effective algorithms.
Various solution approaches like the gradientbased methods, sequential unconstrained minimization technique and dynamic programming have been used to optimize the design of machine elements. The gradientbased methods differ in their reliability, efficiency and sensitivity to the initial solution. Furthermore, they are inclined to obtain a local optimal solution. The gradientbased methods are limited because they are not ideal for non-convex problems.
Convergence speed to the global optimum and solution accuracy are important factors in the development of optimization methods. Since the convergence speed of evolutionary algorithms to the global optimal results is better than that of conventional techniques, non-traditional optimization methods such as genetic algorithm (GA), simulated annealing, particle swarm optimization algorithm, differential evolution and ant colony algorithm have been widely preferred in the solution of optimization problems from design industry.
We can divide the optimization algorithms into two categories. The first category, known as single objective optimization, consists of finding the global maximum or minimum of an objective function which is a function of design variables. A number of benchmark problems on the single objective design optimization such as the design of pressure vessel, welded beam, tension compression spring, gear train, speed reducer, hydro static thrust bearing, step cone pulley, Belleville spring, Rolling element bearing etc have been reported in the literature. The above single objective benchmark problems have been solved by both traditional and nontraditional optimization techniques.
Over the last years, genetic algorithms (GAs) have received a lot of attention as an optimization method in the design of basic machine elements such as springs, gears, pulleys, shafts etc. GA’s work on the natural phenomenon of genetics such as selection, reproduction, crossover and mutation to find the global best solution. The application of GA’s in the design optimization of machine elements such as spring, hollow shaft and belt pulley system is reported in [1]. He et al [2] used improved particle swarm optimization for solving some benchmark problems on single objective design optimization. Rao et al [3] recently proposed teaching learning based optimization (TLBO) for solving single objective design optimization of above mentioned benchmark problems. The second category is multi objective optimization, which embroils the simultaneous optimization of multiple, often conflicting objectives. Instead of finding a single optimal solution, a set of optimal non-dominated solutions is generated; this set is referred to as the Pareto domain. A solution (P) is said to dominate a solution (Q) when (P) is not worse than (Q) in any of its objective function values and it is better with respect to at least one objective. In general, most of the real-world problems are multi objective in nature. Thus in many cases, solving single-objective problem alone does not provide an effective solution. Thus, in this work, we have dealt with multi-objective design optimization problem. As mentioned earlier, a number of research studies are observed on single objective design optimization problems, but there are a few research studies on design optimization problem dealing with multi-objective scenario and even fewer research studies applying evolutionary strategies. A multi-objective optimization problem gives rise to a set of optimal solutions commonly known as Pareto optimal solution [4]. Thus, instead of getting a single solution, we get a set of solutions because of the presence of multiple objectives. The decision maker, then, chooses one or more solutions from among the Pareto optimal solutions.
Multi-objective optimization problem can be solved mathematically or by applying heuristics or metaheuristics. Goal programming is a mathematical technique to solve multi-objective optimization problem [5]. Another way is to solve such problem by multiobjective evolutionary algorithm (MOEA) [6]. Because of the increasing attention toward machine learning procedures, MOEA techniques have gone through considerable evolution. The MOEA techniques can be classified into (1) apriori technique where the decision maker assigns relative importance to the objectives prior to the application of MOEA algorithm; (2) progressive technique which is actually an interactive search method; and (3) a posteriori technique where the decision maker will choose the solution after completion of the search technique. A number of MOEA algorithms are also observed in the existing literature [6]. Some of them are: vector evaluated genetic algorithm [7], weight-based genetic algorithm (GA) [8], multiple objective GA [9], vector optimized evolution strategy [10], strength Pareto evolutionary algorithm (SPEA, SPEA2) [11, 12], Pareto archived evolutionary strategy [13], Pareto envelopebased selection algorithm (PESA, PESA II) [14, [15], niched Pareto GA (NPGA, NPGA 2) [16, 17], multi objective Particle swarm optimization (MOPSO), multi objective differential evolution (MODE) and nondominated sorting GA (NSGA, NSGA-II) [4, 18]. Salim fettaka et al [19] used NSGA II for the multi objective design optimization of a shell-and tube heat exchanger. The two objective functions considered were the heat transfer area and pumping power. Nine decision variables were considered to obtain the multiple Pareto-optimal solutions which capture the trade-off between the two objectives. Murugan et al [20] proposed the application of NSGA II for multi objective generation expansion planning (GEP) problem. They have also introduced two modifications such as Virtual Mapping Procedure (VMP) and controlled elitism in NSGA-II. Ramesh et al [21] used a modified version of NSGA II for multi objective reactive power planning. They have applied the concept of TOPSIS for finding the best solution from the Pareto front solutions obtained using MNSGA II. In this work, we are applying the NSGA II algorithm to solve the disc brake design optimization problem with two conflicting objectives of minimizing both the mass of the brake and stopping time of the brake. The disc brake optimization model has four design variables and five inequality constraints.

II. DISC BRAKES
Modern motor cars are fitted with disc brakes instead of conventional drum type brakes. In Santro car and Maruti-800, front wheels are provided with disc brakes whereas rear wheel are provided with drum brakes. A disc brake consists of a rotating disc and two friction pads which are actuated by hydraulic braking system as described earlier. The friction pads remain free on each side of disc when brakes are no applied. They rub against disc when brakes are applied to stop the vehicle. These brakes are applied in the same manner as that of hydraulic brakes. But mechanism of stopping vehicle is different than that of drum brakes.
image
Advantage of Disc Brakes:
(a) Main advantage of disc brakes is their resistance to wear as the discs remain cool even after repeated brake applications.
(b) Brake pads are easily replaceable.
(c) The condition of brake pads can be checked without much dismantling of brake system.
Disadvantage of Disc Brakes :
(a) More force is needed be applied as the brakes are not self-emerging.
(b) Pad wear is more.
(c) Hand brakes are not effective if disc brakes are used in rear wheels also. (Hand brakes are better with mechanical brakes).

III. OPTIMIZATION
Optimization deals with the study of practical problems in which one has to minimize or maximize with one or more objectives that are functions of some real or integer variables. This is executed in a systematic way by choosing the proper values of real or integer variables within an allowed set. Given a defined domain, the main goal of optimization is to study the means of obtaining the best value of some objective function.
image
Single Objective Optimization:
The study of practical problems in which one has to minimize or maximize with one objective function of some real or integer variables. Different optimization techniques that are found in the literature can be broadly classified into three categories.
• Calculus-based techniques.
• Enumerative techniques.
• Random techniques.
Numerical methods, also called calculus-based methods, use a set of necessary and sufficient conditions that must be satisfied by the solution of the optimization problem.
Multi Objective Optimization:
The study of practical problems in which one has to minimize or maximize with more than one objective functions of some real or integer variables. Different optimization techniques that are found in the literature can be broadly classified into three categories
Multi objective optimization (MOO) recognizes that most of the practical problems invariably require a number of design criteria to be satisfied simultaneously, viz.,
image
ideal “optimal” solution, but a set of Pareto-optimal solutions for which an improvement in one of the design objectives will lead to a degradation in one or more of the remaining objectives. Such solutions are also known as noninferior or nondominated solutions to the MOO problem.
The concept of Pareto-optimality in the twoobjective case is illustrated in Fig. Here, points M and N are two examples of nondominated solutions on the Pareto-front. Neither is preferred to the other. Point M has a smaller value of 2 f than point N, but a larger value of
image
Nondominated Sorting Genetic Algorithm (NSGA-II):
Primary strength of NSGA-II lies in its ease-of-use because of its elitism, nondominated ranking and crowding distance which lead to rapid convergence to very high quality solutions. NSGA-II has been proposed, as a modification of NSGA, to alleviate the three difficulties associated with NSGA. It incorporates elitism, fast nondominated sorting approach and diversity along the Pareto optimal front which is well maintained using a crowding distance operator. Elitism maintains the knowledge acquired during the algorithm execution by conserving the individuals with best fitness in the population.
Initially, a random parent population 0 Ppop is created. The population is sorted based on the nondomination. Each solution is assigned a fitness equal to its nondomination level (1 is the best level). Thus, minimization of fitness is assumed. Tournament selection, recombination, and mutation operators are used to create offspring population 0 Off of size N . Further, the NSGA-II procedure can be outlined in the following steps:
image

IV.PROBLEM DESCRIPTION
Multi-objective disc-brake optimization problem:
The multi-objective disc-brake optimization problem was solved by Osyczka and Kundu [22] using plain stochastic method and genetic algorithms for optimization of disc-brake problem. They have shown that genetic algorithm was giving better results compared with that of plain stochastic method. The objectives of the problem are to minimize the mass of the brake and to minimize the stopping time. The disc brake optimization model has four variables that are
x1- inner radius of the discs, in mm
x2- outer radius of the discs, in mm
x3- engaging force, in N and
x4- number of the friction surfaces (integer)
The objective functions and constraints of the discbrake design optimization model provided by Osyczka and Kundu [22] are defined as follows:
image

V. RESULTS AND DISCUSSION
For demonstration purpose, NSGA II approach is applied on the constrained optimization problem consists of two objectives. The first objective is minimization of the mass of the brake and second one is stopping time. The obtained best results of NSGA II in 10 trials are tabulated. Matlab 7.9 software package is used on a PC compatible with Pentium IV, a 3.2 GHz processor and 3 GB of RAM (Random Access Memory).
Optimal parameter combinations for NSGA II are experimentally determined by conducting a series of experiments with different parameter settings before conducting actual runs. The optimal parameters are given in Table. The population size is set to 50 particles and the maximum generations (set as stopping condition) is set to 2000 generations. A total of 100000 fitness function evaluations were made with this optimization approach in each run.
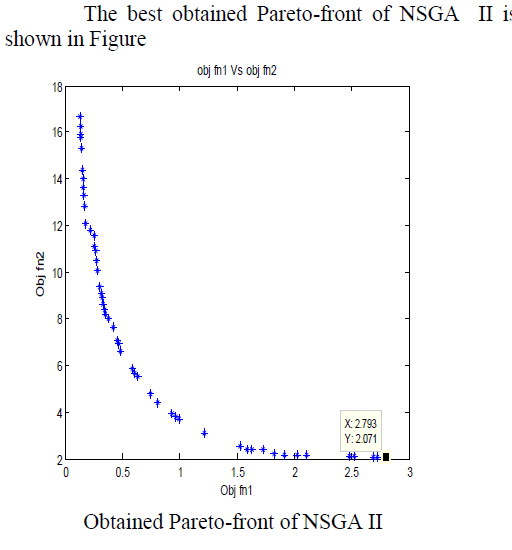image
image
Figure shows that the applied MOEAs are able to generate Pareto-front in a single simulation run. The extreme points of Pareto-front obtained by NSGA II are given in Table.
image

VI.CONCLUSIONS
The bi-objective design optimization of disc brake problem was solved using fast, elitist NSGA II algorithm by considering two objective functions. The results of 50 Pareto fronts are obtained after 2000 iterations are plotted in a graph which shows better optimal solutions. The curve in the graph shows that the results are smooth and are better than the results obtained by other optimization techniques.

References
  1. A K Das & D K Pratihar.: Optimal Design of Machine Elements using a Genetic Algorithms. Journal of Institution of Engineers, 83, pp.97 – 104. (2002).
  2. S. He , E. Prempain & Q. H. Wu, An improved particle swarmoptimizer for mechanical design optimization problems, Engineering Optimization Vol. 36, No. 5, October 2004, 585–605.
  3. Rao, R.V., Savsani, V.J., Vakharia, D.P., 2011. Teaching–learningbased optimization: a novel method for constrained mechanical design optimization problems. Comput. Aided Des. 43 (3), 303–315.
  4. D. Kalyanmoy, P.Amrit, S. Agarwal, T.Meyarivan, A fast and elitist multi objective genetic algorithm: NSGA-II, IEEE Trans. Evol. Comp. 6(2) (2002) 182–197.
  5. Barichard V, Ehrgott M, Gandibleux X, T'Kindt V (eds) (2009) Multi-objective programming and goal programming: theoretical results and practical applications. Springer, Berlin
  6. Coello CA, Lamont GB, Van Veldhuizen DA (2007) Evolutionary algorithms for solving multi-objective problems, 2nd edn. Springer, Berlin
  7. Schaffer JD, Grefenstette JJ (1985) Multiobjective learning via genetic algorithms. Proceedings of the 9th International Joint Conference on Artificial Intelligence (IJCAI-85). Los Angeles, California, AAAI, pp 593–595
  8. Hajela P, Lin CY (1992) Genetic search strategies in multicriterionoptimal design. Struct Optim 4:99–107
  9. Fonseca CM, Fleming PJ (1993) Genetic algorithms for multi objective optimization: formulation, discussion and generalization. In: Forrest S (ed) Proceedings of the Fifth International Conference on Genetic Algorithms, San Mateo, California. University of Illinois at Urbana-Champaign, Morgan Kaufmann Publishers, pp 416–423
  10. Kursawe F (1991) A variant of evolution strategies for vector optimization. In: Schwefel H-P, Männer R (eds) Parallel problem solving from nature. 1st Workshop, PPSN I, Dortmund, Germany, October 1991. Springer, Lecture Notes in Computer Science No. 496, pp 193–197
  11. Zitzler E, Laumanns M, Thiele L (2001) SPEA2: improving the strength Pareto evolutionary algorithm. In: Giannakoglou K, Tsahalis D, Periaux J, Papailou P, Fogarty T (eds) EUROGEN 2001. Evolutionary methods for design, optimization and control with applications to industrial problems, Athens, Greece, pp 95–100
  12. Zitzler E, Thiele L (1999) Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach. IEEE Trans Evol Comput 3(4):257–271 (November 1999)
  13. Knowles JD, Corne DW (2000) Approximating the non dominated front using the Pareto archived evolution strategy. Evol Comput 8 (2):149–172
  14. Corne DW, Jerram NR, Knowles JD, Oates MJ (2001) PESA-II: region based selection in evolutionary multiobjective optimization. In:Spector L, Goodman ED,Wu A, LangdonW, Voigt H-M, GenM, Sen S,DorigoM, Pezeshk S,GarzonMH, Burke E (eds) Proceedings of the genetic and evolutionary computation conference (GECCO’2001). Morgan Kaufmann, San Francisco, pp 283–290
  15. Corne DW, Knowles JD (2003) No free lunch and free leftovers theorems for multiobjective optimisation problems. In: Fonseca CM, Fleming PJ, Zitzler E, Deb K, Thiele L (eds) Evolutionary multicriterion optimization. Second International Conference, EMO 2003, Faro, Portugal, April 2003. Springer, Lecture Notes in ComputerScience, vol 2632, pp 327–341
  16. Erickson M, Mayer A, Horn J (2001) The niched Pareto genetic algorithm 2 applied to the design of groundwater remediation systems. In: Zitzler E, Deb K, Thiele L, Coello Coello CA, Corne D (eds) First International Conference on Evolutionary Multi-Criterion Optimization.Springer, Lecture Notes in Computer Science No. 1993, pp 681–695
  17. Horn J, Nafpliotis N, Goldberg DE (1994) A niched Pareto genetic algorithm for multiobjective optimization. Proceedings of the First IEEE Conference on Evolutionary Computation, IEEE World Congress on Computational Intelligence, vol 1, Piscataway,New Jersey, June 1994.IEEE Service Center, pp 82–87
  18. Srinivas N, Deb K (1994) Multiobjective optimization using non dominated sorting in genetic algorithms. Evol Comput 2 (3):221–248
  19. Salim Fettaka, Jules Thibault, Yash Gupta, Design of shell-and-tube heat exchangers using multi objective optimization, International Journal of Heat and Mass Transfer 60 (2013) 343–354
  20. P. Murugan, S. Kannan, S. Baskar, NSGA-II algorithm for multi objective generation expansion planning problem, Electric Power Systems Research 79 (2009) 622–628
  21. S. Ramesh, S. Kannan, S. Baskar , Application of modified NSGAII algorithm to multi-objective reactive power planning, Applied Soft Computing 12 (2012) 741–753
  22. Osyczka, A., Kundu, S.,1996. A modified distance method for multi criteria optimization using genetic algorithms. Computers and Industrial Engineering 30, 871–882.
  23. Ray L, Liew KM. A swarm metaphor for multi objective design optimization. Engineering Optimization 2002; 34(2):141–53.
  24. Ali R. Yıldız & Nursel Öztürk & Necmettin Kaya & Ferruh Öztürk, Hybrid multi-objective shape design optimization using Taguchi’s method and genetic algorithm, Struct Multidisc Optim (2007) 34:317–332
  25. Ali Rıza Yıldız, An effective hybrid immune-hill climbing optimization approach for solving design and manufacturing optimization problems in industry, journal of materials processing technology 209 ( 2009 ) 2773–2780
  26. Xin-She Yang, Suash Deb, Multi objective cuckoo search for design optimization, Computers & Operations Research 40 (2013) 1616–1624
  27. Xin-She Yang, Multi objective firefly algorithm for continuous optimization, Engineering with Computers (2013) 29:175–184
  28. Xin-She Yang, Mehmet Karamanoglu, Xingshi He, Multi-objective Flower Algorithm for Optimization, Procedia Computer Science 18 (2013 ) 861 – 868
  29. Gilberto Reynoso-Meza, Xavier Blasco, Javier Sanchis, Juan  M.Herrero, Comparison of design concepts in multi-criteria decisionmaking using level diagrams, Information Sciences 221 (2013) 124–141
  30. D.Kalyanmoy,Multi-Objective Optimization using Evolutionary Algorithms, John Wiley & Sons Ltd., Singapore, 2001 (ISBN 9814-12-685-3).
  31. D. Kalyanmoy, An efficient constraint handling method for genetic algorithms ,Computer methods in Applied Mechanics and Engineering 186 (2) (2000) 311–338.
  32. K. Deb, A. Anand, D. Joshi, A computationally efficient evolutionary algorithm for real-parameter optimization, Evol. Comp. J.10 (4) (2002) 371–395.
  33. Coello, C.A.C. “Recent trends in evolutionary multi objective optimization”, Evolutionary Multi objective Optimization Theoretical Advances and Applications, Springer-Verlag, London, pp.7-32, 2005.
  34. Deb, K. Multi-objective optimization using Evolutionary Algorithms, Wiley, Chichester, UK, 2001.
  35. Luo, B., Zheng, J., Xie, J. and Wu, J. “Dynamic crowding distance– a new diversity maintenance strategy for MOEAs”, In Proc. of theIEEE Int. Conf. on Natural Computation, pp. 580-585, 2008.