ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
E.K.R.Nagarajan1 and P.Geetha 2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Soft set theory was introduced by Molodtsov in 1999 as a mathematical tool for dealing with problems that contain uncertainty. Faruk Karaaslan et al.[6] defined the concept of soft lattices, modular soft lattices and distributive soft lattice over a collection of soft sets. In this paper, we define the concept of principle of duality in soft lattices and discuss some related properties of modular and distributive soft lattices. We also establish characterization theorems for modular and distributive soft lattices by their soft sublattices.
Keywords |
| Soft sets, soft lattices, soft sublattices, dual soft lattices, modular soft lattices, distributive soft lattices. |
INTRODUCTION |
| Soft set theory was introduced by Molodtsov [9] in 1999 as a mathematical tool for dealing with uncertainty. Maji et al.[8] defined some operations on soft sets and proved related properties. Irfan Ali et al.[5] studied some new operations on soft sets. Li [7], Nagarajan et al.[10] defined the soft lattices using soft sets. Faruk Karaaslan et al.[6] defined the concept of soft lattices over a collection of soft sets by using the operations of soft sets defined by Cagman et al.[1]. In this paper, we define the concept of principle of duality in soft lattices and discuss some related properties of modular and distributive soft lattices. We also illustrate them with some examples. In addition, we establish characterization theorems for modular and distributive soft lattices by their soft sublattices. |
SOME CONCEPTS IN SOFT SETS AND SOFT LATTICES |
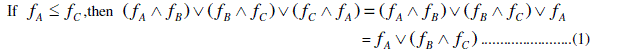 |
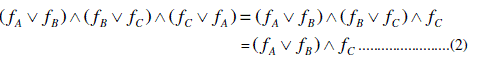 |
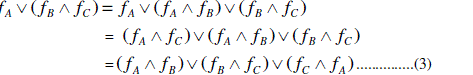 |
MODULAR AND DISTRIBUTIVE SOFT LATTICES |
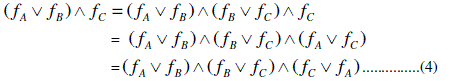 |
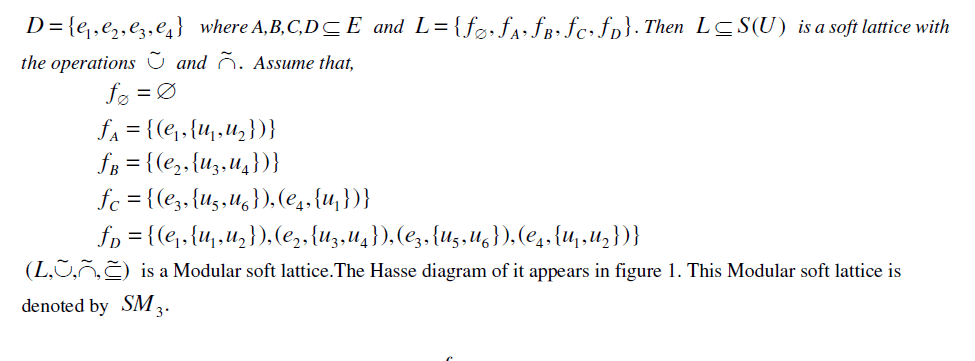 |
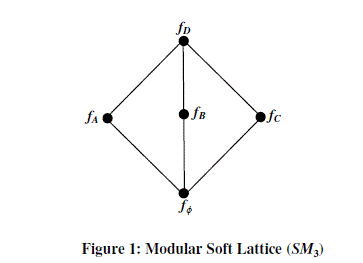 |
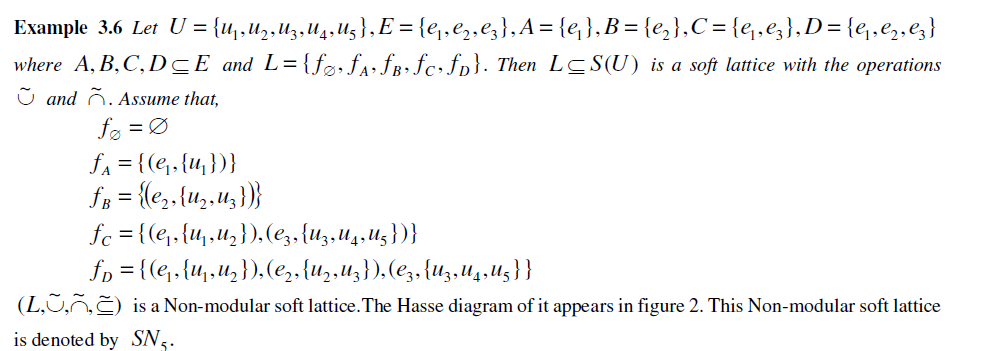 |
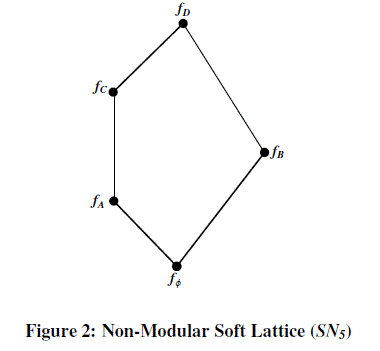 |
 |
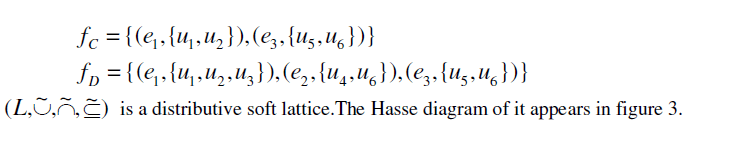 |
 |
 |
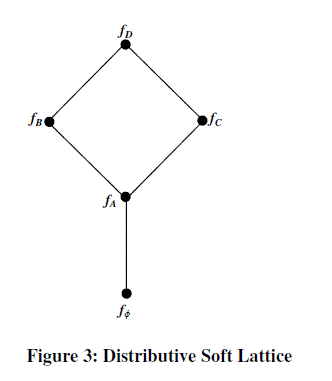
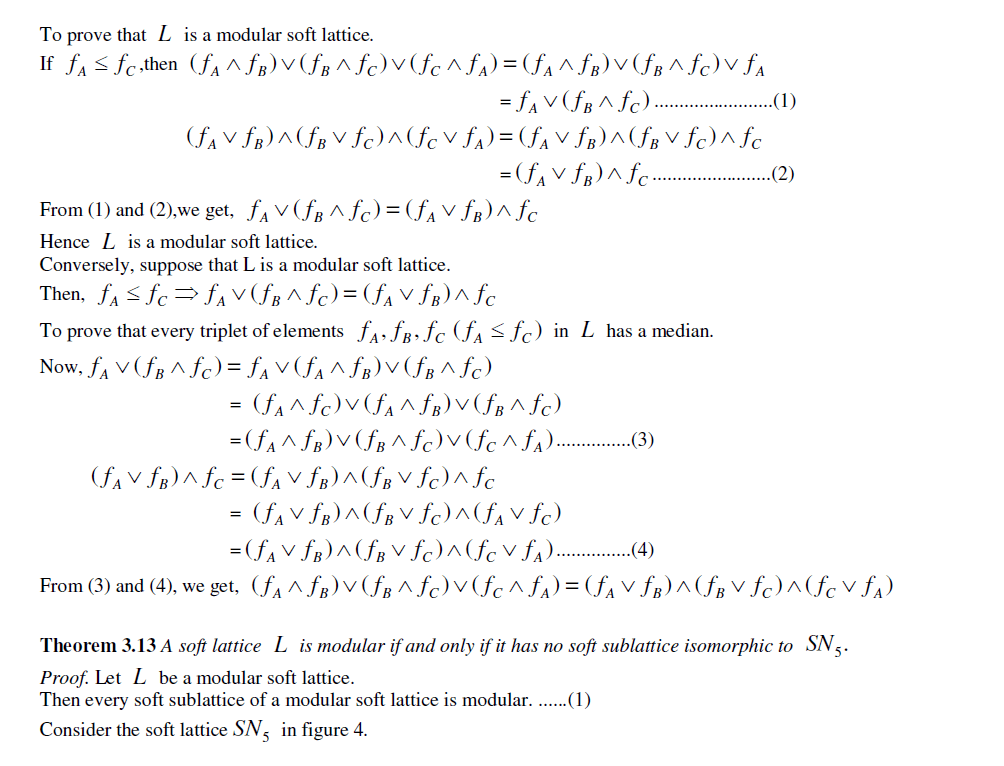 |
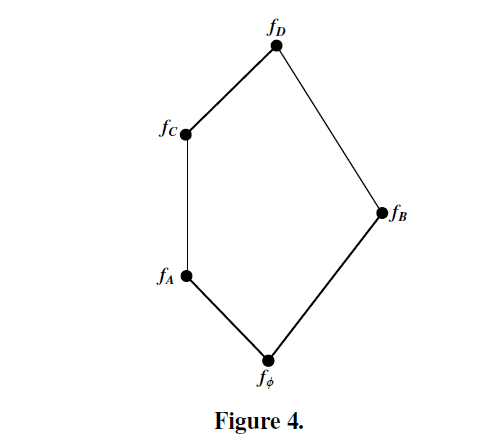 |
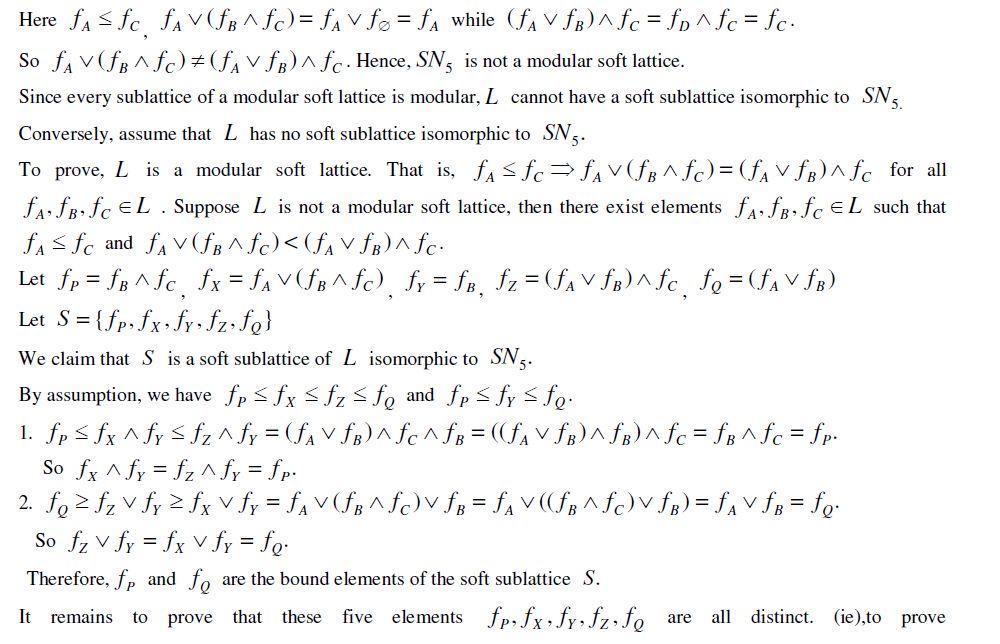 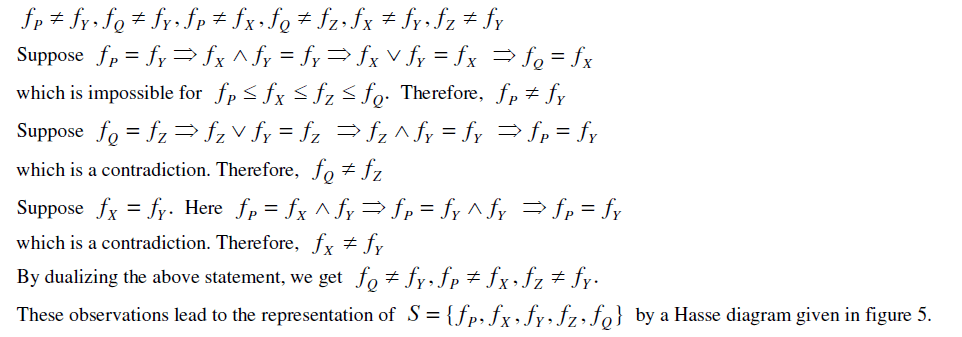 |
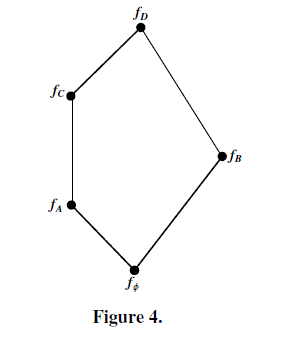 |
 the distributive soft lattice is distributive. the distributive soft lattice is distributive. |
 |
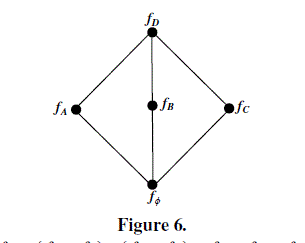
| distributive soft lattice. Consider 3 SM in figure 6. |
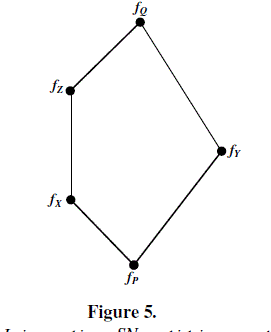 |
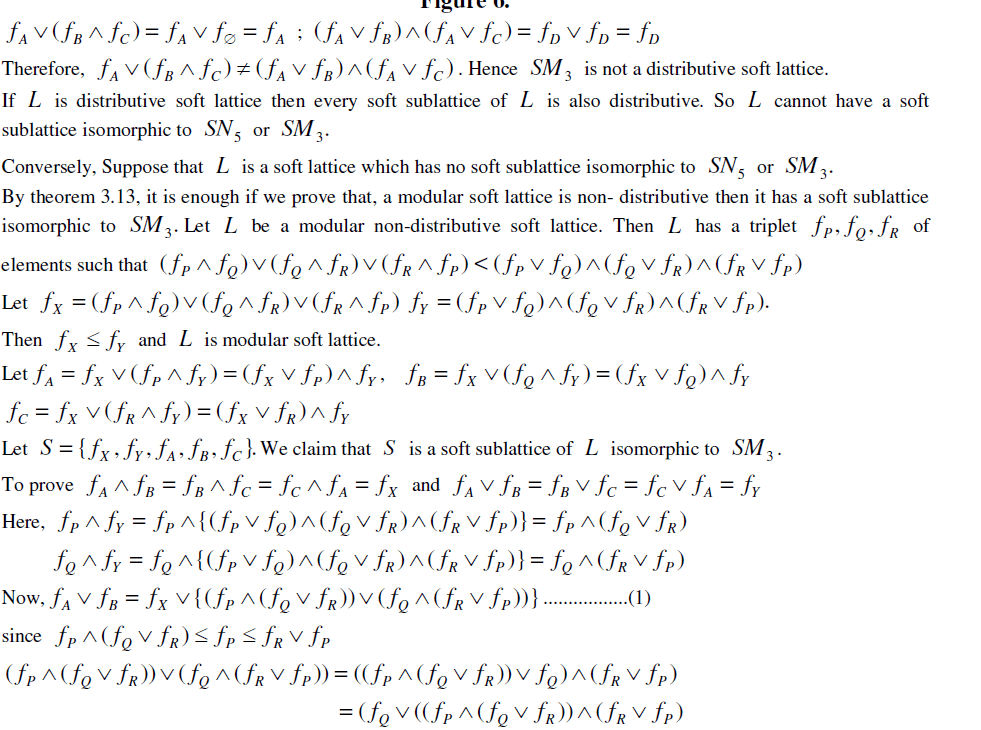 |
 |
 |
 |
CONCLUSION |
| In this paper, we have given characterization theorems for modular soft lattices and distributive soft lattices.We are studying about these soft lattices and are expected to give some more results. |
References |
|