ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
K. Sakthi Madhavan1, M. Ruth Jenila2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In wireless communication for better transmission, single carrier waves are being replaced by multi carrier signals. OFDM system divides high speed serial information signal into multiple lower speed sub-signal. Orthogonally spaced sub carriers are used to carry the data from the transmitter end to the receiver end in high speed wireless system. Orthogonality is used between sub carriers to avoid ICI (Inter Carrier interference). But the large Peak to Average Power Ratio of these signal have some undesirable effects on Orthogonal Frequency Division multiplexing system. The orthogonal sub carriers will increase high PAPR value. High PAPR will lead complexity in real time implementation OFDM. The existing system analyses the performance of PAPR reduction scheme through conventional methods. The basic idea of existing algorithm is to divide the original OFDM sequence into several sub-sequences and for each sub-sequences multiplied by different weights until an optimum value is chosen. This will lead to high complexity and also increase the number of iteration. In this paper we proposed genetic algorithm for peak-average-power ratio (PAPR) reduction and also reduce its complexity by reducing the number of iterations.
Keywords |
| OFDM, PAPR, BER, CCDF, Genetic approach, Subcarrier(SC) |
OFDM |
| Due to development of mobile communication, wireless system need to face a heavy demand of highly efficient and high speed communication. OFDM is a multicarrier modulation technology which is used in broadband wireless communication systems like WiMAX, DVB-T and future 4G/LTE systems because it has high spectral efficiency and less complexity in construction of receiver. OFDM is an effective multicarrier transmission technique for wireless communications over frequency selective channels using an inverse fast Fourier transform (IFFT) and a fast Fourier transform (FFT) for the baseband modulation and demodulation, This model shows time and frequency characteristics of an OFDM signal with 1024 subcarriers. As the OFDM signal is the sum of a large number of independent, identically distributed components its amplitude distribution becomes approximately Gaussian due to the central limit theorem. Therefore, it suffers from large peak-to-average power ratios. |
 |
PAPR |
| One of the main disadvantages of the OFDM systems is the high PAPR of the transmitted signal due to the combination of N modulated SCs. An OFDM signal consists of orthogonal subcarriers modulated by parallel data streams. Each baseband subcarrier is of the form |
 |
 |
| A.PAPR on OFDM |
| Generate all possible combinations of weighting factor set in the IFFT block. PAPR is defined as the ratio between the maximum instantaneous power and its average power. At last only optimization will be achieved. The PAPR for a continuous-time signal, x(t), is defined as |
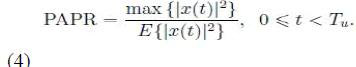 |
| On the other hand, the PAPR for discrete-time signals can be estimated by oversampling the data sequence d depicted in Fig.1 by a factor L and computing LN-points IFFT of the data block with (L − 1)N zeropadding. The PAPR in this case is defined as |
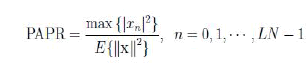 |
| B.CCDF of the PAPR |
| The CCDF is widely used to assess the performance of PAPR reduction techniques which is defined as the probability that the PAPR is greater than a reference value denoted as PAPR0. The CCDF of the PAPR of the OFDM signals with N = 1024 SCs and different oversampled factor, L = 1, 2 and 4. It is clear that the PAPR does not increase considerably after L = 4. Therefore, an accurate PAPR estimation for the discrete model requires an oversampling factor L > 4. It has been shown that the difference between the continuous-time and discrete-time PAPR is negligible for L = 4 [31]. |
| A straightforward estimated expression for the CCDF of the PAPR of an OFDM signal with Nyquist rate sampling was derived in [32]. For an OFDM signal with a large number of SCs and from the central limit theorem, the real and imaginary parts of N-point IFFT output samples have a mutually independent and uncorrelated Gaussian probability distribution function with zero mean and a variance of σ2 = E{|xn|2}/2. Furthermore, the amplitude of the OFDM signal has a Rayleigh distribution, whereas the power distribution can be characterized by a central chi-square distribution with two degrees of freedom. The cumulative distribution function (CDF) of this distribution is given by |
 |
| it can be seen that the CCDF expression is not precise for a small number of SCs; for large values of N > 128 this expression is more precise. |
GENETIC APPROACH |
| Assume we have a discrete search space and a function The general problem is to find where the function It is usually desirable that c should be a bijection. (The important property of a bijection is that it has an inverse, i.e., there is a unique vector x for every string s, and a unique string s for every vector x.) In some cases the nature of this mapping itself creates difficulties for a GA in solving optimization problems. Here x is a vector of decision variables, and f is the objective function. We assume here that the problem is one of minimization, but the modifications necessary for a maximization problem are nearly always obvious. Such a problem is commonly called discrete or combinatorial optimization problems (COP). One of the distinctive features of the GA approach is to allow the separation of the representation of the problem from the actual variables in which it was originally formulated. |
| Choose an initial population of chromosomes; While termination condition not satisfied do |
| repeat |
| If crossover condition satisfied then |
| [select parent chromosomes; |
| choose crossover parameters; |
| perform crossover]; |
| While mutation condition satisfied then |
| choose mutation points; |
| perform mutation]; |
| evaluate fitness of offspring |
| until sufficient offspring created; |
| select new population; |
| endwhile |
| A.Representation of the Variable |
| In line with biological usage of the terms, it has become customary to distinguish the ‘genotype’—the encoded representation of the variables, from the ‘phenotype’—the set of variables themselves. That is, the vector x is represented by a string s, of length l, made up of symbols drawn from an alphabet , using a mapping In practice, we may need to use a search space to reflect the fact that some strings in the image of under c may represent invalid solutions to the original problem. The string length l depends on the dimensions of both and and the elements of the string correspond to ‘genes’, and the values those genes can take to ‘alleles’. This is often designated as the genotype–phenotype mapping. |
| B. Chromosomes |
| The original motivation for the GA approach was a biological analogy. In the selective breeding of plants or animals, for example, offspring are sought that have certain desirable characteristics—characteristics that are determined at the genetic level by the way the parents’ chromosomes combine. In the case of GAs, a population of strings is used, and these strings are often referred to in the GA literature as chromosomes. |
| The recombination of strings is carried out using simple analogies of genetic crossover and mutation, and the search is guided by the results of evaluating the objective function f for each string in the population. Based on this evaluation, strings that have higher fitness (i.e., represent better solutions) can be identified, and these are given more opportunity to breed. It is also relevant to point out here that fitness is not necessarily to be identified simply with the composition f(c(s)); more generally, fitness is h(f(c(s))) where is a monotonic function. |
| Perhaps the most fundamental characteristic of genetic algorithms is that their use of populations of many strings. Holland also used mutation, but in his scheme it is generally treated as subordinate to crossover. Thus, in Holland’s GA, instead of the search moving from point to point as in NS approaches, the whole set of strings undergoes ‘reproduction’ in order to generate a new population. |
| DeJong’s work established that population-based GAs using crossover and mutation operators could successfully deal with optimization problems of several different types, and in the years since this work was published, the application of GAs to COPs has grown almost exponentially. These operators and some developments of them are described more fully in part B. Crossover is a matter of replacing some of the genes in one parent by corresponding genes of the other. An example of one-point crossover would be the following. Given the parents P1 and P2, with crossover point 3 (indicated by X), the offspring will be the pair 01 and 02: |
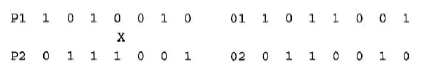 |
| The other common operator is mutation, in which a subset of genes is chosen randomly and the allele value of the chosen genes is changed. In the case of binary strings, this simply means complementing the chosen bits. For example, the string 01 above, with genes 3 and 5 mutated, would become 1 0 0 1 1 0 1 . A simple template for the operation of a genetic algorithm is shown in Figure 3.1. The individual parts of this very general formulation will be discussed in detail in Part B. |
| C. Crossover |
| Here again, the German school of ES initially did not use populations, and focused almost exclusively on ‘mutation’ operators which are generally closer in concept to the types of operator used in neighborhood search and its extensions. Crossover is simply a matter of replacing some of the genes in one parent by the corresponding genes of the other. Suppose we have 2 strings a and b, each consisting of 6 variables, i.e. which represent two possible solutions to a problem. (Note that we have chosen here to leave the alphabet unspecified, to emphasize that binary representation is not a critical aspect of GAs.) One-point crossover (1X) has been described earlier; two-point crossover (denoted by 2X), is very similar. Two cross points are chosen at random from the numbers and a new solution produced by combining the pieces of the the original ‘parents’. For instance, if the cross points were 2 and 4, the ‘offspring’ solutions would be |
| D. Mutation |
| Firstly, we note that in the case when crossover- OR-mutation is used, we must first decide whether any mutation is carried out at all. Assuming that it is, the concept of mutation is even simpler than crossover, and again, this can easily be represented as a bit-string. We generate a mask such as |
| using a Bernoulli distribution at each locus— with a small value of p in this case. (The above example would then imply that the 2nd and 6th genes are assigned new allele values.) However, there are different ways of implementing this simple idea that can make a substantial difference to the performance of a GA. The naive idea would be to draw a random number for every gene in the string and compare it to but this is potentially expensive in terms of computation if the strings are long and the population is large. An efficient alternative is to draw a random variate from a Poisson distribution with parameter where is the average number of mutations per chromosome. |
| A common value for is 1—in other words, if l is the string length, the (bit-wise) mutation rate is which as early as 1964 [85] was shown to be in some sense an ‘optimal’ mutation rate. Having decided that there are (say) m mutations, we draw m random numbers (without replacement) uniformly distributed between 1 and l in order to specify the loci where mutation is to take place. |
| E. New population |
| Holland’s original GA assumed a generational approach: selection, recombination and mutation were applied to a population of M chromosomes until a new set of M individuals had been generated. This set then became the new population. From an optimization viewpoint this seems an odd thing to do—we may have spent considerable effort obtaining a good solution, only to run the risk of throwing it away and thus preventing it from taking part in further reproduction. For this reason, De Jong [5] introduced the concepts of élitism and population overlaps. His ideas are simple—an elitist strategy ensures the survival of the best individual so far by preserving it and replacing only the remaining (M – 1) members of the population with new strings. |
| Overlapping populations take this a stage further by replacing only a fraction G (the generation gap) of the population at each generation. Finally, taking this to its logical conclusion produces the so-called steady-state or incremental strategies, in which only one new chromosome (or sometimes a pair) is generated at each stage. |
| D. Random Numbers |
| As GAs are stochastic in nature, it is clear that a reliable random number source is very important. Most computer systems have built-in rand () functions, and that is the usual method of generating random numbers. Not all random number generators are reliable, however, as Ross [95] has pointed out, and it is a good idea to use one that has been thoroughly tested, such as those described in the Numerical Recipes series. |
OPTIMIZATION OF GENETIC APPROACH WITH OTHER TECHNIQUE |
 |
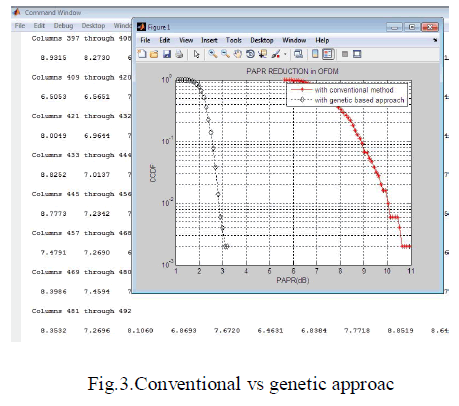 |
CONCLUSION AND FUTURE WORK |
| This paper perused the concept of covered the basic principles of GAs, the number of variations that have been suggested is enormous. Many variations in population size, in initialization methods, in fitness definition, in selection and replacement strategies, in crossover and mutation are obviously possible. This can add information such as age, or artificial tags, to chromosomes; in order to reduce complexity further. |
References |
|