ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
D Mahaboob Valli 1, DR. TK Jindal 2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Pulse detonation engine technology has recently emerged as a future aerospace propulsion technology. In this paper we studied various parameters affecting the performance of Pulse detonation engine (PDE) like pulse detonation engine Tube diameter (combustion tube), Pulse tube length for proper deflagration to detonation transition (DDT),Cell size, Equivalence ratio of fuel used . The Structural aspects like materials for fabrication of pulse detonation engine which can withstand very high pressures, temperature, yield stress and toughness is analysed. We discussed various techniques for reducing the length of pulse tube by using various DDT enhancing devices like Shchelkin spiral, grooved metal sleeves, slotted sleeves etc.
Keywords |
| Pulse detonation engine, Deflagration to detonation (DDT), Schelkin spiral, Cell size (λ). |
INTRODUCTION |
| Pulse Detonation Engines (PDEs) are new concept propulsion systems that utilize repetitive detonations to produce thrust or power. Pulse Detonation engines offers the potential to provide increased performance while simultaneously reducing the engine weight, cost and complexity relative to conventional propulsion systems currently in service. Due to its obvious advantages, worldwide attention has been paid to the scientific and technical issues concerning Pulse Detonation Engine. Despite extensive research in Pulse Detonation Engine over the past several decades, it is not yet to be used practical propulsion applications. (4-6) |
| One of the key barriers to the realisation of an operational Pulse Detonation Engine lies in the difficulty to ignite the detonation wave in the engine in a reliable and controllable manner. This barrier is particularly critical for application that involves hydrocarbon/air mixture since it is well known that detonations are difficult to achieve with in a practical length in hydrocarbon/air mixtures, which are less sensitive to detonation initiation taking atomization, vaporization and detonation into account. Detonation can be initiated either directly or by deflagration flame acceleration followed by deflagration to detonation transition (DDT). Direct detonation initiation energy and power requirement are a function of Cell Size or Cell Width, of a detonable mixture, which is the measure of the combustion reaction rates of the fuel mixture. Minimum energies are approximately 260000 joules for several hydrocarbon/air mixtures which are prohibitive for practical Pulse Detonation engines. It is desirable to use low initiation energy system to produce fully developed detonations with in an acceptable distance (7). The objective of this study is to investigate how the parameters affecting the performance of the pulse detonation Engine. |
II. LITERATURE SURVEY |
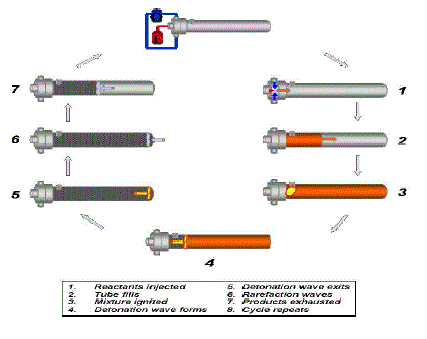
| The operation of a single cycle pulse detonation engine consists of four major steps |
| (i) Filling of tube with the desired mixture |
| (ii) Detonation initiation |
| (iii) Propagation of the detonation along the tube |
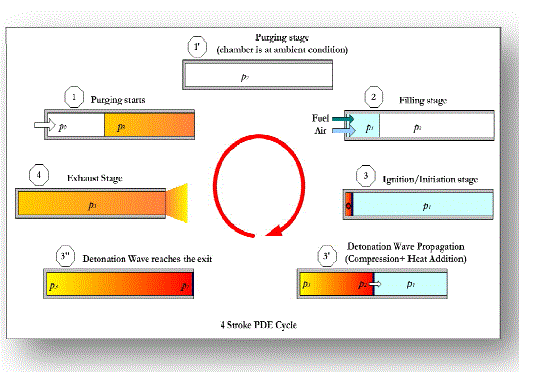 |
| A detonation wave is a supersonic combustion wave consisting of a shockwave coupled with a reaction zone. The conditions behind an ideal detonation wave are dictated by the Chapman –Jouguet (CJ) conditions that the flow behind wave be in sonic in a reference frame moving with the detonation velocity. A detonation wave therefore propagates at a unique velocity (Ucj) which is a function of mixture composition and the initial thermodynamic conditions .This velocity (Ucj) and other properties such as (Pcj) behind the detonation wave can be compounded given the thermodynamic properties of the initial mixture and the products. |
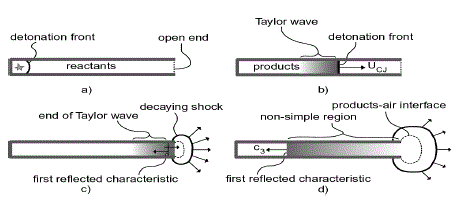
III. IDEAL PDE OPERATION CYCLE: |
| For an ideal situation the initiation process takes only a short time and the detonation wave is quickly established, propagating near the CJ velocity. A detonation wave propagating in a closed end tube is followed by an isentropic expansion wave (Taylor wave) that brings the flow to rest at some distance behind the detonation wave .The pressure decreases to a value of P3 at the end of the tube ,the detonation is propagating and for short period of time afterwards. When the detonation wave reaches the open end of the tube the detonation process ceases since there is no fuel outside the tube. The detonation products flow out of the tube creating a shockwave in the external region and a series of expansion waves are reflected back into the tube. As the tube is emptied the pressure decreases to equal the ambient value, often with an intermediate excursion to sub ambient values. |
 |
| For the purpose of estimating impulse, only the pressure at the closed end of the tube must be known. The thrust or the force on the tube can be found by integrating the pressure over the area of end wall. The pressure on the thrust wall consists of a negligible excursion to the Chapman-Jouguet pressure peak (Pcj) a constant pressure P3 regime and decreasing pressure associated with exhaust process(8). |
| The simplest way to characterize the performance of an Ideal Cycle is to integrate the thrust over the duration of the cycle to obtain the Impulse. The resulting Impulse can be expressed in at least two ways. |
| (i) Impulse per unit volume (Iv) and |
| (ii) Impulse per unit mass or Specific Impulse (Isp) |
| The Impulse per unit volume (Iv) is independent of tube size . The Impulse per unit volume (Iv) is directly proportional to Plateau Pressure (P3) and inversely proportional to detonation velocity. |
| Iv =Δ P3 [1/Ucj+(α+β)1/C3] |
| Where α&β are two non dimensional parameters characteristic of constant and decaying part of pressure signal and ΔP3 and C3 are the over pressure and sound speed of products after the Taylor wave (9). |
| The Specific Impulse (Isp) is commonly used as a figure of merit in the propulsion community and is defined as |
 |
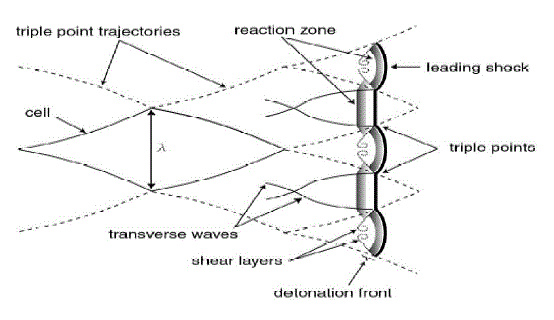
| DETONATION CELL WIDTH (λ): The cell width, of a detonation is defined as the width of a cell formed by the slipstream associated with the interaction of the transverse and longitudinal waves of the detonation or as the average transverse wave spacing recorded on a sooted foil, is a useful measure of detonation. Generally speaking, the smaller the cell width, the smaller the minimum energy required to initiate detonation. The cell width can also be empirically related to other dynamic parameters such as the minimum tube diameter that is required for detonation propagation. Detonation cell size is also a measure of the sensitivity of the mixture to detonate .Table 1 shows a comparison of select fuels and their cell size. Although mathematical models to predict cell size exist, their poor accuracy favors values obtained experimentally. |
 |
| The energy required to achieve a detonation can be shown to be directly related to the cell size of a detonation wave structure. The energy required to initiate a hydrocarbon fuel detonation can be on the order of 1 MJ whereas the detonation energy for hydrogen and air is generally around 5000 J (Tucker et al, 2004:18). A relationship of initiation energy to cell size can be experimentally determined to be given by (Schauer et al, 2005:2): |
| E initiation = 3.375λ3 |
| Using air or oxygen as the oxidizer the above relationship shows that the initiation energy drops by the cube of the cell size. Fuels using pure oxygen as an oxidizer require less initiation energy than fuels in a diluted oxygen environment such as air. It is possible using the above relationship to show that minimum initiation energy to achieve a detonation directly correlates with deflagration to detonation transition (DDT) time for a fuel air mixture. Furthermore, if it is possible to relate cell size to initial pressure it possible to relate initiation energy to initial pressure for a given temperature and equivalence ratio. |
| DETONATIONTUBE DIAMETER (d): A detonation typically cannot propagate in a tube of diameter less than the Cell Size (λ) divided by Π the limit corresponding to highly unstable or spinning detonations. |
| d < λ/Π Ã¢Ãâ¢ÃÂ> detonation cannot propagate (spinning detonation) |
| Where d= Dia of detonation tube, |
| λ = Cell Size |
| This corresponds to a minimum diameter of about 0.75 inch. A more realistic limit is associated with transition to detonation which usually requires that the “minimum detonation tube size is about one cell width which is nearly equal to 2.4 inch” (10). |
| DETONATION TUBE LENGTH (L): Another parameter affecting detonation is that the detonation tube should be long enough so that the detonation has the time to be successfully initiated (3). This is especially true if the detonation is deflagration to detonation transition (DDT). A rough estimate of the “minimum length required for detonation initiation and stabilization is 10 λ or 23.6 inch. |
 |
RELATION BETWEEN DETONATION TUBE DIAMETER (d) AND LENGTH (L): |
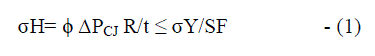 |
| DETONATION SENSITIVITY: The customary measure of detonation sensitivity is the “Cell Width (λ)”. This is one of the constraints that determines the minimum detonation tube diameter (d) and detonation tube length (L).Data from earlier experiments shows that by a careful Igniter design it is possible to initiate a mixture with sensitivity (Stoichiometric Acetylene –Oxygen mixture λ=55mm) comparable to JP-10-air and obtain nearly ideal performance with a tube of diameter 3 inch and a length of 40 inch. These dimensions are substantially larger than the minimum dimensions. If sensitivity of mixture could be increased i.e Cell Width decreased, then the Pulse Detonation Engine could be shorter and run at higher frequency. This could be achieved by either |
| (a) Using more sensitive mixture |
| (b) By sensitizing the initial Acetylene-Oxygen (C2H2-O2) mixture |
| EQUIVALENCE RATIO OF FUEL- OXIDIZER MIXTURE (φ): Combustion of fuel oxidizer mixture is specified in terms of “Equivalence ratio” (φ). The equivalence ratio is independent of mass (m) or the number of moles (n) that is used to characterize the proportion of fuel to oxidizer mixture. Equivalence ratio is defined as “The ratio of the fuel – oxidizer ratio to the Stoichiometric fuel–oxidizer ratio. Equivalence ratio can be mathematically represented as Equivalence Ratio |
| (φ):= m fuel /m oxidizer / (m fuel /m oxidizer) stoichiometric = n fuel/n oxidizer / (n fuel/n oxidizer) stoichiometric |
| The composition and the thermodynamic properties of fuel oxidizer mixture during combustion/detonation are dependent on the Equivalence Ratio. The composition and the thermodynamic properties of fuel oxidizer mixture during combustion/detonation are dependent on the “Detonation Cell Width” if the wave propagates at supersonic speeds. Equivalence ratio (φ) greater than 1 would imply excess fuel or rich mixtures than would be required for stoichiometric reaction and conversely Equivalence ratio (φ) less than 1 would imply excess oxidizer or fuel lean mixtures. The detonable mixture’s Equivalence ratio is an important factor in how rapidly it was able to transition into detonation. Optimized Equivalence ratio for every condition lies from range of Φ’s from 0.9 to 1.2. There is a sharp increase in XDDT for φ’s less than 0.75. Pulse detonation engine with it’s specific mixture at Equivalence Ratio (φ)’s slightly greater than stoichiometric, would minimize the detonation transition distance. |
 |
V. STRUCTURAL CONSIDERATIONS |
| MATERIAL: The choice of material must account for the environment and the required durability. Many material properties must be known before confidence can be placed in the selection of material. These properties include hardness, tensile, compressive strengths, Young’s Modulus, Poisson’s ratio, creep rates, oxidation and corrosion rates, fatigue strength and fatigue crack propagation rate (all as function of time, temperature, and heat treatment). In this paper we randomly selected four materials (SiliconNitrideSi3N4, 6061T6 Aluminium, 4340 Steel, and Inconel 718) some room temperature properties of these materials are given in table. |
 |
| Out of the above four material Silicon Nitride is potentially of interest because of its high strength to weight ratio and high temperature properties. However it has low fracture toughness. Aluminium is a typical aerospace construction material and is widely used in prototype engines. However it has poor high temperature properties. 4340 steel is tough steel that is widely used in pressure vessel applications. Inconel 718 is a high temperature material that is widely used in gas turbine construction. |
| YIELD STRESS: The Maximum principle stress on an internally pressurised thin walled cylinder is the hoop stress (σH). One of the key design constraints for a tube to withstand an internal detonation pressure is to limit the dynamic hoop stress at a certain safety factor below the tensile yield stress of the material, ensuring that no permanent plastic deformation develops. The maximum dynamic hoop stress constraint can be expressed as |
| σH= ÃÂÃ⢠ΔPCJ R/t ≤ σY/SF - (1) |
| where σY is the tensile yield stress of the tube material ,SF is the safety factor, σH is the amplitude of the dynamic hoop stress, ÃÂÃ⢠is the dynamic amplification factor, ΔPCJ = PCJâÃâÃâ¬Po, PCJ is the Chapman-Jouguet pressure, Po is the ambient pressure external to the tube, R is the tube mean radius and t is the wall thickness. Note that ΔPCJ R/t is the usual static strength of materials estimation of the hoop stress. Since the internal pressure is dynamic, a `dynamic amplification factor' ÃÂÃ⢠has to multiply the static hoop stress to obtain the dynamic hoop stress. The dynamic load factor (1 ≤ ÃÂÃ⢠≤ 4) is a function of the detonation wave velocity. If the material, safety factor, and mixture are selected, then the remaining variables are the tube radius and wall thickness. For an `SF = 3' design of a tube closed at the ignition end and open at the exhaust end. Further, we assume that there is no reflected shock wave and that there are no holes or flaws on the tube. Once a material is selected (so that ¾Y is fixed), then Eq. 1 implies that the tube thickness has to scale with the radius |
| R α t - (2) |
| The design criterion of a specified thrust (impulse), implies that the thickness has to decrease as the length L increases according to |
| t α 1/√ fL |
| Eq. 1 also implies that the thrust-to-weight ratio is proportional to the ratio f σY / ρ. Maximizing the thrust-to-weight ratio at a fixed repetition frequency corresponds to maximizing σY / ρ. This is known as yield-limited design and is the standard design principle for pressure vessels of minimum weight. |
VI. RESULTS AND DISCUSSIONS: |
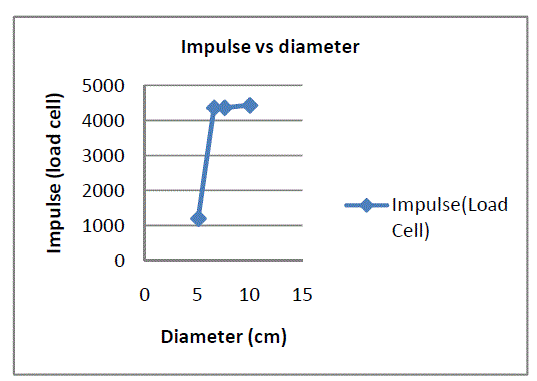
| EFFECTS OF PDE DIAMETER (d): Effects of PDE diameter on its performance were examined. Fully developed CJ detonation waves were successfully attained. The pressure peak at location 1 is about 15.6 atm, which is near the value of CJ detonation and indicates the DDT distance in this case is less than 240 mm. The comparison of the pressure profiles obviously demonstrates the similarity between them. It was measured that for 30mm diameter PDE model the average thrust was 20Ncompared to 72.9N for 56 mm diameter PDE at 10Hz operation. The results verify that the average thrust increases with diameter. |
| EFFECTS OF PDE LENGTH (L): It is of great importance for practical PDE to shorten its length. Decreasing PDE model length from 2m to 1m was successfully realised by means of strong swirling mixing and effective turbulence enhancement. It was found that the peak pressure at thrust wall for PDE model with 2m length were 30%larger than that of 1m length. This result indicates the relaxation process has great effect on PDE impulse. Since the impulse depends upon the area bounded by the pressure history curves and abscissa. The impulse is larger for slower relaxation process. It is inferred that a longer tube will have a larger impulse but lower accessible detonation frequency and larger PDE weight. There should be an Optimum length of PDE which would be the compromise among impulse, weight and accessible detonation frequency. |
| EFFECT OF EQUIVALENCE RATIO (φ): Detonation velocities versus equivalence ratio in 30 mm diameter PDE model at detonation frequency 6 Hz are presented in fig. The detonation velocity increases with Equivalence ratio until 1.4, which consists with theoretical analysis. The measured detonation velocities are 1-5% less than the theoretical ones due to two phase effects. The reason is that for two phase mixtures, there are two factors to decrease detonation velocity, evaporation of atomized droplets. This needs absorbing heat, and the heterogeneity of mixing fuel vapour with air. |
VII. CONCLUSIONS |
| (1) The PDE test rig designed and developed by PEC, Department of Aerospace Engineering PDE Research team is a single shot PDE with 60mm diameter with 250cm length which produces 280 N. |
| 2) An efficient and reliable technique of detonation initiation with low energy initiation system (50mj) was developed by means of strong swirling mixing and effective turbulence enhancement by means of schelkin spiral. Solenoid valves were used to adaptively control intermittent supply of acetylene and oxygen flows. |
| (3) The effects of PDE diameter, length and equivalence ratio on its performance were studied. The results demonstrated that the average thrust of PDE is approximately proportional to the volume of detonation chamber and detonation frequency. The Max average thrust for 60mm diameter is 280 N. |
References |
|