ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
1Pravin Kumar Borkar, 2 Manoj Jha, 3M. F. Qureshi, 4G.K.Agrawal
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Performance monitoring system for shell and tube heat exchanger is developed using Mamdani Adaptive Neuro-Fuzzy Inference System (M-ANFIS). Experiments are conducted based on full factorial design of experiments to develop a model using the parameters such as temperatures and flow rates. M-ANFIS model for overall heat transfer coefficient of a design /clean heat exchanger system is developed. The developed model is validated and tested by comparing the results with the experimental results. This model is used to assess the performance of heat exchanger with the real/fouled system. The performance degradation is expressed using fouling factor (FF), which is derived from the overall heat transfer coefficient of design system and real system. Hybrid algorithm is the hot issue in Computational Intelligence (CI) study. From in-depth discussion on Simulation Mechanism Based (SMB) classification method and composite patterns, this paper presents the Mamdani model based Adaptive Neural Fuzzy Inference System (M-ANFIS) and weight updating formula in consideration with qualitative representation of inference consequent parts in fuzzy neural networks. M-ANFIS model adopts Mamdani fuzzy inference system which has advantages in consequent part. Experiment results of applying M-ANFIS to evaluate Reliable Performance Assessment of Heat Exchanger show that M-ANFIS, as a new hybrid algorithm in computational intelligence, has great advantages in non-linear modeling, membership functions in consequent parts, scale of training data and amount of adjusted parameters. This paper proposes a new perspective and methodology to model the fouling factor (FF) of the heat exchanger using the fuzzy reliability theory. We propose to use the indicator or performance or substitute variable which is very well understood by the power plant engineer to fuzzify the states of heat exchanger
Keywords |
| Heat exchanger; Overall heat transfer coefficient; Fouling factor (FF), Fuzzy reliability, performance characteristics, Mamdani Adaptive Neuro-Fuzzy Inference System (M-ANFIS). |
INTRODUCTION |
| Heat exchanger process is complex due to its nonlinear dynamics and particularly the variable steady state gain and time constant with the process fluid (Mandanvgane et al 2006). Heat exchangers are used to transfer the heat between two fluids across a solid surface that are at different temperatures. The commonly used shell and tube heat exchangers are used in refrigeration, power generation, heating, air conditioning ,chemical processes, manufacturing and medical applications (Ozcelik , 2007)). The performance of heat exchanger deteriorates with time due to formation of fouling on heat transfer surface. It is a very complicated phenomenon and can be broadly categorized into particulate, corrosion, biological, crystallization, chemical reaction and freeze. It is necessary to assess periodically the heat exchanger performance, in order to maintain at high efficiency level. Performance of heat exchanger is monitored by the following methods: i) Outlet temperature of the hot stream (Tho) profile, ii) Approach temperature (Tho - Tci) profile, iii) Log Mean Temperature Difference (LMTD) with time, iv) Heat load profile, and v) Time series of overall heat transfer coefficient. The first four methods are widely used and are ineffective in terms of isolating the net impact of fouling from process upsets. But the overall heat transfer coefficient method requires detailed calculations and knowledge of the geometry of the exchangers (Radhakrishnan et al 2007) Any deviation from the heat transfer coefficient of design/clean heat exchanger will indicate the occurrence of fouling( Vijaysa et al 2006). Tubular Exchanger Manufacturing Association recommends an allowable fouling factor (FF) or fouling resistance to tolerate some degree of fouling before cleaning must be undertaken. Hence, monitoring system is needed to assess the performance of heat exchanger. In experimental studies and engineering applications of thermal science, researchers and engineers are expected to reduce experimental data into one or more simple and compact dimensionless heat transfer correlations (Wang et al 2006). The limitations of correlation methods are addressed by computational intelligent (CI) techniques, such as M-ANFIS and fuzzy reliability. M-ANFIS is one of the most powerful computer modeling techniques, based on fuzzy approach, currently being used in many fields of engineering for modeling complex relationships which are difficult to describe with physical models. |
| In this paper, a performance monitoring system is developed for a shell-and-tube heat exchanger using secondary measurements namely the temperatures and flow rates of the hot and cold fluid (water).Experimental system is developed to investigate the performance of heat exchanger. M-ANFIS is applied to model the heat exchanger with experimental data. The input parameters to develop a model for design/clean heat exchanger are inlet temperature and flow rate of shell and tube side fluids and output is overall heat transfer coefficient (UDesign). The overall heat transfer coefficient of real/fouled system (UReal) is calculated using measured values such as inlet temperature, outlet temperature and flow rate of shell and tube side fluids. The heat exchanger performance is assessed by comparing the results of clean/design and fouled/real system. Any deviation from the result of design/clean system indicates that the performance is degraded due to fouling. Its degree of membership is derived from fouling factor (FF) using UDesign and UReal. A Mamdani model based Adaptive Neural Fuzzy Inference System, which named M-ANFIS is proposed here. Experimental results show that this model can achieve the desired targets and have a preferable capacity in performance assessment of heat exchanger. |
| This paper proposes to use the theory and methods for fuzzy sets to model the reliability for a system with continuous stochastic performance degradation. We use the performance characteristic variable which indicates the continuous performance levels of degradable systems to fuzzify the states of a component or system. The engineering or technological performance variable is well understood by the system designers and can be used to represent different degrees of success. Thus, the imprecision in the meaning of success/failure is quantified through the fuzzy success/failure membership function which is defined over the performance characteristic variable. The proposed fuzzy reliability measures provide an alternative to model the continuous state behavior for a system. The dynamic behavior of fuzzy reliability is investigated using the concept of fuzzy random variable under appropriate stochastic performance degradation processes. |
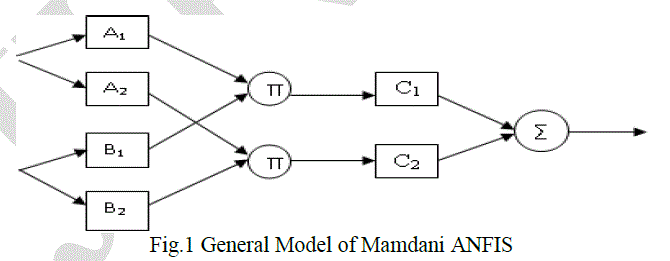
MAMDANI BASED ADAPTIVE NEURO FUZZY INFERENCE SYSTEM (M-ANFIS) |
| This paper presents a class of adaptive neural network equivalent of Mamdani fizzy inference system in its function, which named M-ANFIS. It means adaptive network based fuzzy inference system. Neural network has the great function of dealing with imprecise data by training, while fuzzy logic can deal with the uncertainty of human cognition. The nature of these two methods is a universal approximator and they have the function of non-linear modeling. In fact, neural networks and fuzzy logic have fused very well. Fuzzy neural networks implement main steps of fuzzy inference in an ordered layers of a neural network with an architecture such that the weights to be adjusted in the network, which makes fuzzy inference more closer to actual situation by learning capability of NN. FNN are widely used in a lot of areas. Jang has brought forward Sugeno fuzzy inference model-based ANFIS. This paper will introduce a Mamdani model based Adaptive Neural Fuzzy Inference System (M-ANFIS), which has greater superiority to ANFIS in expression of consequent part and intuitive of fuzzy reasoning. This model will reflect nature of CI much more. The details will be introduced in the following section. |
| Model Description |
| The T-S fuzzy inference system works well with linear techniques and guarantees continuity of the output surface (Tan et al 2009). But the T-S fuzzy inference system has difficulties in dealing with the multi-parameter synthetic evaluation; it has difficulties in assigning weight to each input and fuzzy rules. Mamdani model can show its legibility and understandability to the lay people. The Mamdani fuzzy inference system shows its advantage in output expression and is used in this project. We derive the following theorem. Advantages of applying such composite inference methods are that such Mamdani ANFIS model has the ability of learning because of differentiability during computation. The sum-product composition provides the following theorem (Yang et al 2000), see in Eq.1 and Eq.2. Final crisp output when using centroid defuzzification is equal to weighted average of centroids of consequent MFs, where: |
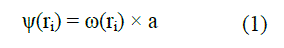 |
 |
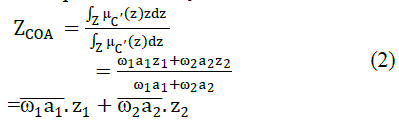 |
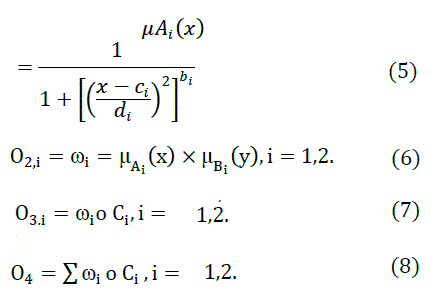 |
| Weight Updating Formula |
| Weight updating formulas are very important for adjusting M-ANFIS model parameters. In this section, we conclude the weight updating formula for M-ANFIS model by discussing the general weight updating formula based on basic idea of back propagation in NN. An adaptive network is a network structure whose overall input-output behavior is determined by a collection of modifiable parameters (Yang et al 2000). A feed forward adaptive network is a static mapping between its inputs and output spaces. Our goal is to construct a network for achieving a desired nonlinear mapping. This nonlinear mapping is regulated by a data set consisting of desired input-output pairs of a target system to be modeled: this data set is called training data set. The procedures that adjust the parameters to improve the network’s performance are called the learning rules. A learning rule explains how these parameters (or weights) should be updated to minimize a predefined error measure. The error measure computes the discrepancy between the network’s actual output and a desired output (Yuanyuan et al 2009). The steepest descent method is used as a basic learning rule. It is also called back-propagation (Cheng et al., 1993). Our task is to minimize an overall error measure defined as: |
 |
MODELING OF HEAT EXCHANGER USING M-ANFIS |
| In order to verify the validity of M-ANFIS model of heat exchanger presented in this paper, we apply this M-ANFIS into the evaluation UDesign of heat exchanger. Through training and testing this model by historical sample data, the results indicate that this model has ability of mapping heat exchange input data to the value of overall heat transfer coefficient designed UDesign. In the mean time, it is illuminated that M-ANFIS model shows great superiority to ANFIS model according to the experiments results analysis between them. Sample data in this experiment are supported by power plant expert engineers. All these data are obtained by experts confirm and are reliable. |
| Overall heat transfer coefficient Designed UDesign Evaluation |
| In heat exchanger system, UDesign is a quality measure describing operational conditions within a system. Now a day in power plant evaluation of UDesign is a fundamental factor for reliable performance decision-making. Basic sensor data (such as Thi- hot water inlet temperature, flow rate of cold water Fci and flow rate of hot water Fhi) are obtained by detector and are effective for UDesign synthetic evaluation. All these data are divided into training data and testing data. According to potential mapping relation between UDesign and those three indices, we apply this M-ANFIS to UDesign evaluation. Consequently, experiments by these sample data shows that the M-ANFIS model introduced in this paper provide theoretical basis and a new methodology for multi-inputs synthetic UDesign evaluating. |
| M-ANFIS model |
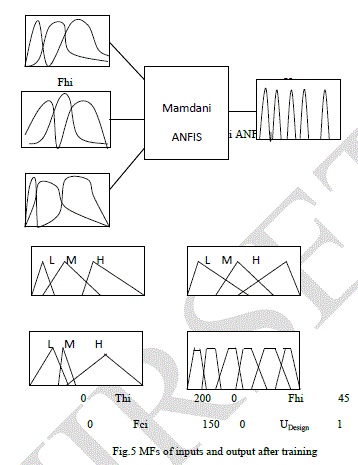
| In ANFIS, the output of each rule is a linear combination of input variables plus a constant term, and the final output is the weighted average of each rule’s output. UDesign reflects the operator’s subjective feelings on the heat exchanger; obviously the above model can’t reflect the true nature of UDesign because of its linear output. M-ANFIS model is able to resolve this issue because grades of UDesign in consequent part are expressed as membership function rather than a simple linear equation. M model reflects the true meaning of UDesign and logic reasoning of operator. In Fig.3, the evaluating process of UDesign is illustrated. Consequently, we construct the following model. See in Fig.4. In this model, x, y, z represents the input, which is Thi, Fci and Fhi. A1-A3 represents membership functions of Thi; B1-B3 represents membership functions of Fci; C1-C3 |
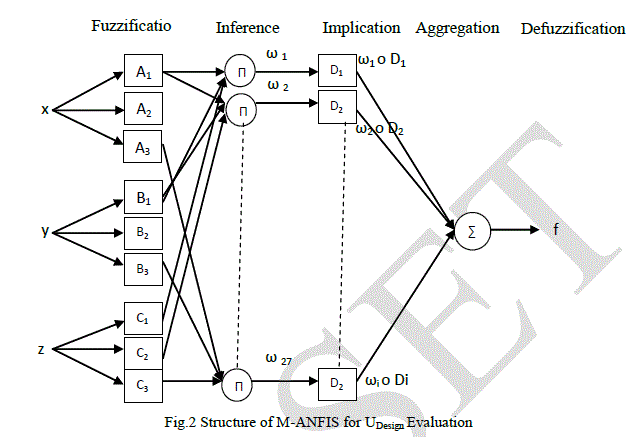 |
| represents membership functions of Fhi. D1-D6 represents membership functions of UDesign output. Rule’s format is: |
| Rule 1: If x is A1 and y is B1 and z is C1, then UDesign =A. |
| In this model, premise parameters are 27 and consequent parameters are 24, which are all nonlinear parameters. We adjust all these parameters in M-ANFIS based on the weights updating formula, which is shown in Eq.16 and Eq.17. All procedures are implemented with Matlab 7.1. The experiment on evaluating UDesign chooses 2000 pairs sample data (1500 pairs for training and 500 for testing). |
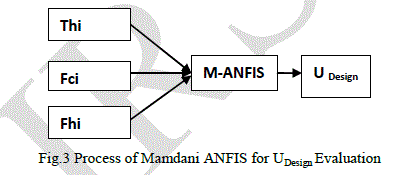
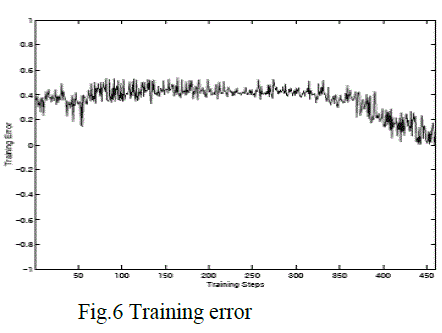
| The training process takes 0.55 second and 500 steps. The mean square error is 0.0003. The training errors are shown in Fig.6. The desired output and real output of M-ANFIS are in Fig.7. Testing errors are in Fig.8. Average test error is 0.0412. Indices of ANFIS and M-ANFIS are in Table 1. From this table , we can conclude that M-ANFIS model is superior to ANFIS in amount of adjusted parameters, scale of training data ,consume time and testing error. Training error satisfies |
 |
| the requirements. It is clear that M-ANFIS is more effective subject to small-scale sample data. In the experiment, MANFIS, with 6 MFs in the consequent part, reflect the essence of UDesign precisely. |
 |
EXPERIMENTAL SET-UP |
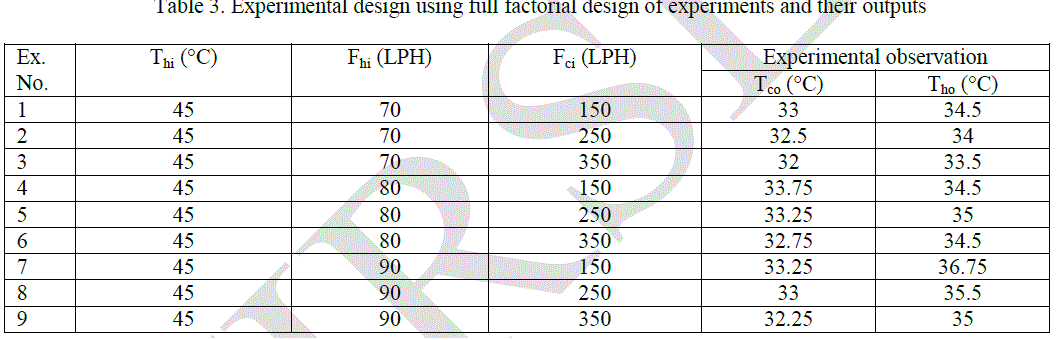
| Experiments are conducted on a 1-1 shell and tube heat exchanger. Cold and hot water flow into the shell and tubes respectively can be changed using pneumatic control valves. The inlet flow of the cold water can be varied in the range of 0 - 400 liter per hour (LPH) and that of hot water between 0 and 300 LPH. The flow rate of cold and hot water were measured using flow transmitter. In experimental design, three levels of process parameters hot water inlet temperature, cold water flow rate and hot water flow rate were selected and are tabulated in Table 2. In this study, full factorial design of experiments is used and their experimental combinations of process parameters were presented in Table 3. The overhead tank water temperature is set initially as 45°C, cold water flow rate as 150 LPH and hot water flow rate as 70 LPH. In this set condition, the process was continued until it reaches the steady state. In steady state, the outlet temperatures of cold and hot water are observed. The flow rate of cold water was changed to 250 LPH and 350 LPH and continues the process to reach steady state. Then the outlet temperatures of cold and hot water were observed. The above step can be repeated by changing the hot water flow rate to 80 LPH and 90 LPH and the outlet temperatures were observed. Similarly for the hot water inlet temperature |
 |
| 55°C and 65°C the above procedure was repeated and the readings were observed. Based on the experimental design combination experiments were conducted for water – hot water system and their results are tabulated in the Table 3. The performance of the heat exchanger is assessed by computing overall heat transfer coefficient. The overall heat transfer coefficient is calculated using log mean temperature difference (LMTD) approach because the inlet temperature, outlet temperature and flow rate of the cold and hot water are known. The overall heat transfer coefficient of shell and tube heat exchanger is calculated by using below equations. |
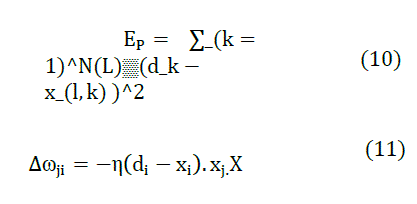 |
| Where Qh - heat transfer rate of hot water side, Qc - heat transfer rate of cold water side, mh - mass flow rate of hot water in kg/hr, mc - mass flow rate of cold water in kg/hr, Cph – specific heat capacity of hot water in kJ/kgK, Cpc – specific heat capacity of hot water in kJ/kgK, Thi – hot water inlet temperature in °C, Tho - hot water outlet temperature in °C, Tco - cold water inlet temperature in °C, Tci - cold water outlet temperature in °C, A - Heat transfer Area in m2 |
 |
DESIGN AND DEVELOPMENT OF PERFORMANCE ASSESSMENT SYSTEM FOR HEAT EXCHANGER |
| Design of performance assessment system |
| A monitoring system for shell and tube heat exchanger was designed based on the current need to evaluate the performance. In this an M-ANFIS is used to develop the model for predicting the overall heat transfer coefficient (UDesign) of the design system using secondary measurements temperature and flow rates. Inputs of the developed network were Thi- hot water inlet temperature , flow rate of cold water Fci and flow rate of hot water Fhi and output was UDesign. Data acquired from the design of experiments were used for training, validation and testing the M-ANFIS model. Heat transfer coefficient of real system (UReal) is derived using secondary measurements such as Tci, Thi, Tco, Tho, Fci and Fhi. This system imitate the real time system and used for performance assessment (fouling) of the system. Measured values of Tci, Thi, Tco, Tho, Fci and Fhi are used to predict the value of UDesign and compute the value of UReal. FF value is computed with the predicted value of UDesign and the computed value of UReal. It is used to identify the performance degradation or degree of fouling of the heat exchanger. If the FF value is greater than or equal to the set value (allowable) of design heat exchanger, warning message will be given for cleaning or maintenance of heat exchanger and the heat exchanger continue to work and monitor the system. Otherwise no warning message will be given and the heat exchanger continues to work and monitor the system. The proposed scheme and flow chart of the online performance monitoring system is shown in Fig.9. |
 |
| M-ANFIS model development |
| Thi, Fci and Fhi and one neuron in the output layer, corresponding to the process response UDesign. The topography of the M-ANFIS model for UDesign is shown in Fig.2. and the developed model in MATLAB environment is shown in Fig.3. |
 |
 |
| Experimental data set are used to train, validate and test the UDesign network. The variation of MSE during the training is shown in Fig.10. The graphical output of M-ANFIS is shown in Fig.13 for UDesign. It is observed that predicted values of UDesign are very closer to the actual values that are shown in Fig.12. It is also found that maximum absolute error of UDesign is 3.46 % is tabulated in Table 4. This indicates that the model accuracy for predicting the process responses is well adequate. For testing, other three new data set are used which do not belong to the training and validation data set. For this testing data set, the overall heat transfer coefficient is predicted using the M-ANFIS model and then compared with the actual values. It is observed that predicted values of UDesign are very closer to the actual values that are shown in Fig.13. It is also found that maximum absolute error of UDesign is 2.54 % is presented in Table 6. |
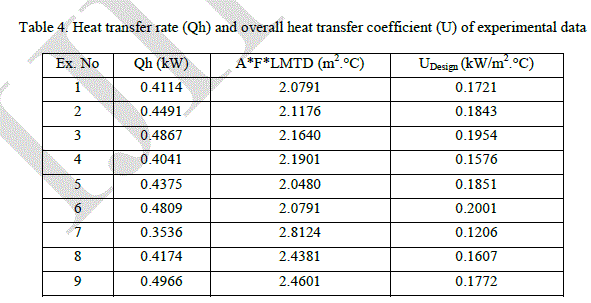 |
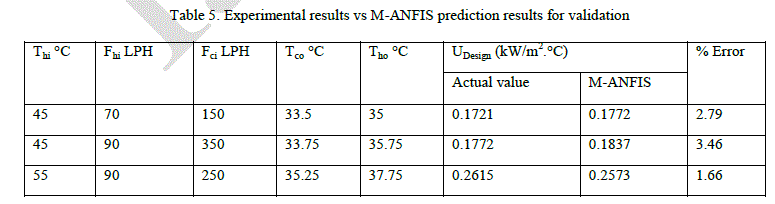 |
| This indicates that the model for predicting the process responses is well adequate for generalization. M-ANFIS model for UDesign is developed to study the performance degradation by estimating the fouling of the shell and tube heat exchanger. |
| Performance assessment |
| Effective and majorly applied method for fouling detection is to compare the UDesign and UReal. It cannot be measured directly and it uses the secondary measurements such as flow rates and temperatures as inputs from the experimental data to estimate it. From the online measured values such as Tci, Thi, Tco, Tho, Fci and Fhi the performance of the heat exchanger is assessed. Thi, Fci and Fhi were used to predict the value of UDesign using developed M-ANFIS model. The consequent part of M-ANFIS is fuzzy in nature and its defuzzyfication gives the crisp value of UDesign. UReal value is computed using LMTD approach with Tci, Thi, Tco, Tho, Fci and Fhi. The performance of heat exchanger is assessed by comparing the UReal value with UDesign value. The decrease in UReal value indicates the degradation of performance by formation of fouling. In this, performance degradation or fouling is estimated using FF approach and this will indicate the degree of fouling. The degradation in performance is expressed by the FF, as calculated by the equation: |
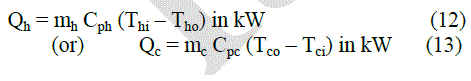 |
DYNAMIC FUZZY RELIABILITY MODELING |
| The success and failure are treated as fuzzy events, which contains continuous performance characteristic values exhibiting different degrees of success or failure. The dynamic fuzzy reliability of a component depends on time and it can be evaluated as the probability of the fuzzy event of success (Zadeh, 1968). Thus fuzzy reliability is defined as: |
| RSUDesign= Pr [fuzzy success] = ∫ μSUDesign (y) dF (y(t) = E [μSUDesign (Y)] (21) |
| Similarly Fuzzy unreliability is defined in terms of the fuzzy failure event as: RFUDesign= Pr [fuzzy failure] = ∫ μFUDesign (y) dF(y(t)= E[μFUDesign (Y)] (22) μFUDesign (y) = 1- μSUDesign (y), and E [μSUDesign (Y)] is a function of time. μSUDesign = Membership function of overall heat transfer coefficient (UDesign) for success μFUDesign = Membership function of overall heat transfer coefficient (UDesign) for failure |
 |
RESULTS AND DISCUSSION |
| The proposed performance monitoring scheme is implemented in the developed experimental setup located in the process lab. The data of heat exchanger such as Tci, Tco, Thi, Tho, Fci and Fhi are captured by running the MATLAB program in PC, which is connected to the data acquisition system. The system initially predicts the UDesign value with M-ANFIS model and dynamic fuzzy reliability model and computes the UReal value through the experimental observed values. The dynamic reliability for success and failure events of UDesign are calculated using dynamic reliability modeling formulae. Then the system computed the FF value using UReal and UDesign values. Based on the FF value the system gives the information to the operator. The results of the system for typical condition are shown in table 6. Here for FF<Set FF=Not Alarming, and for FF>Set FF=Alarming. |
 |
| From the results it is identified that the heat exchanger performance is within the tolerance value (set by field engineer/maintenance engineer) of FF. It shows no warning message to field engineers. Another typical condition results are shown in table 6. This inferred that the performance of the heat exchanger is above the tolerance value of FF. It needs immediate maintenance or corrective action to recover the heat transfer efficiency. This gives intimation to the operator for planning maintenance well ahead to minimize operational disturbance due to unplanned shutdowns. |
CONCLUSION |
| ANFIS, introduced by R. Jang, is the most popular one. In the process of fuzzy inference, ANFIS adopts a linear equation in consequent part, which cannot exhibit human’s judgment reasonably. So, we propose the Mamdani model based adaptive fuzzy inference system (M-ANFIS),which has greater superiority in consequent part and intuitive of fuzzy reasoning. M-ANFIS is a universal approximator because of its infinite approximating capability by training. All parameters in M-ANFIS are nonlinear parameters which can be adjusted by learning rules discussed above. M-ANFIS model can show its legibility and understandability and exhibit the essence of fuzzy logic more clearly. Finally, we use M-ANFIS into Performance Assessment of Heat Exchanger. The experimental results show that M-ANFIS model is superior to ANFIS in amount of adjusted parameters, scale of training data ,consume time and testing error. Experiments were conducted on a 1-1 shell and tube heat exchanger with different cold water flow rates, hot water flow rate, and hot water inlet temperature to assess the performance of the system. The experimental observations were incorporated into the M-ANFIS model development. A M-ANFIS model was developed to predict overall heat transfer coefficient UDesign of the design heat exchanger system and the model was trained, validated and tested for generalization. Good agreement was identified between the predictive model results and the experimental results. MANFIS model was used to predict the value UDesign and UReal was derived from measured values. A dynamic fuzzy reliability model is proposed to evaluate the reliable value of UDesign for the reliable performance assessment of heat exchanger in terms of FF. It is shown that fuzzy modeling is more realistic for systems with continuous performance levels. FF is found from the predicted UDesign and UReal value. From the estimated FF value, the performance degradation/fouling effect was within the tolerance limit (margin) or not is identified. Based on the results, degree of fouling and precaution information like warning or maintenance was given. Further, it needs intelligent approach to do fouling analysis and maintenance decision. |
References |
|