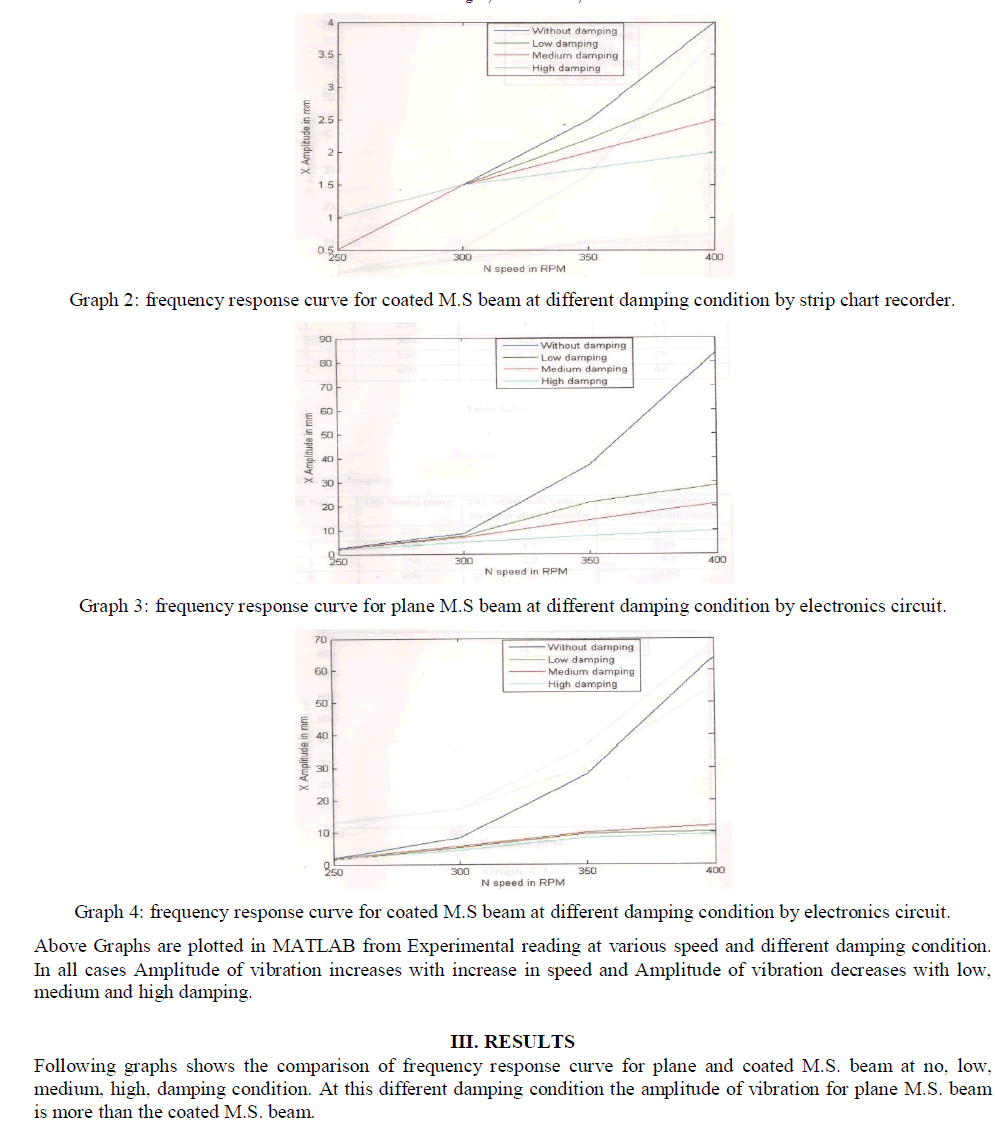
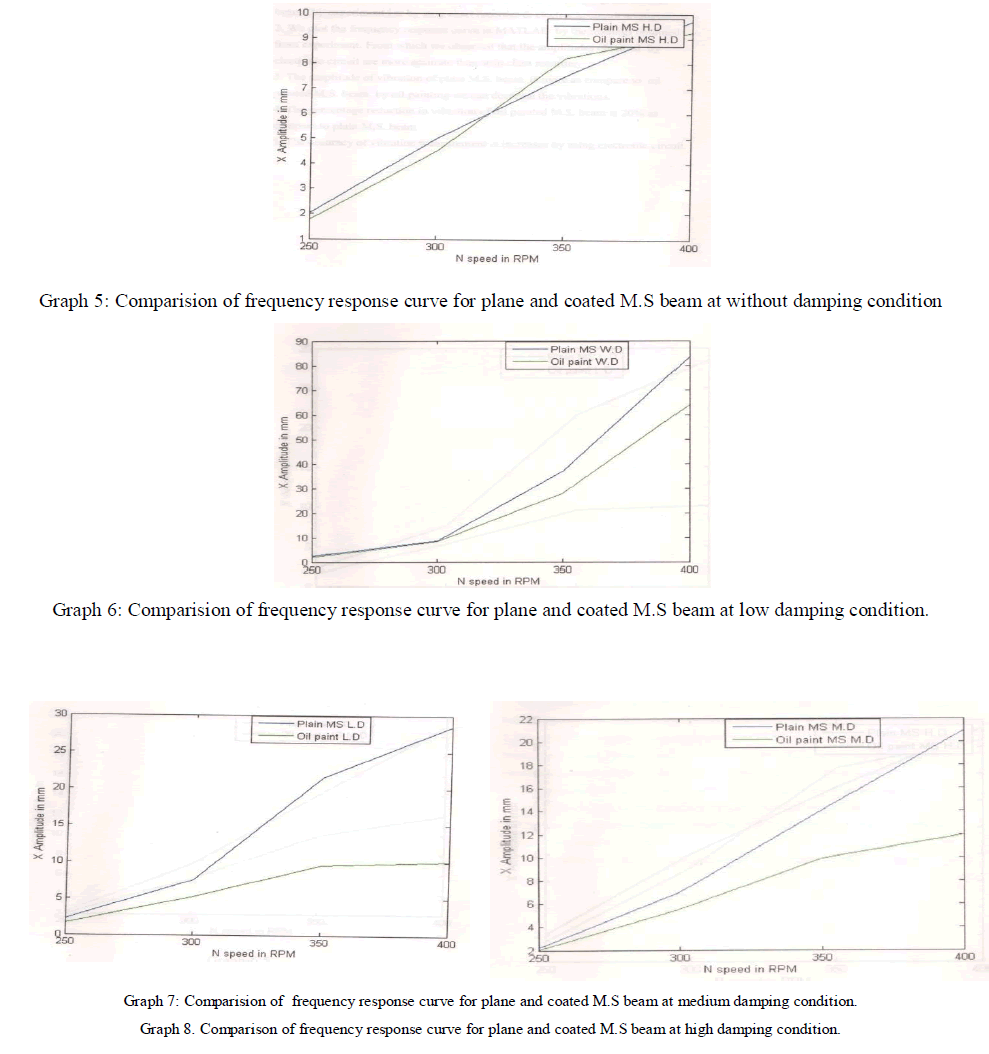
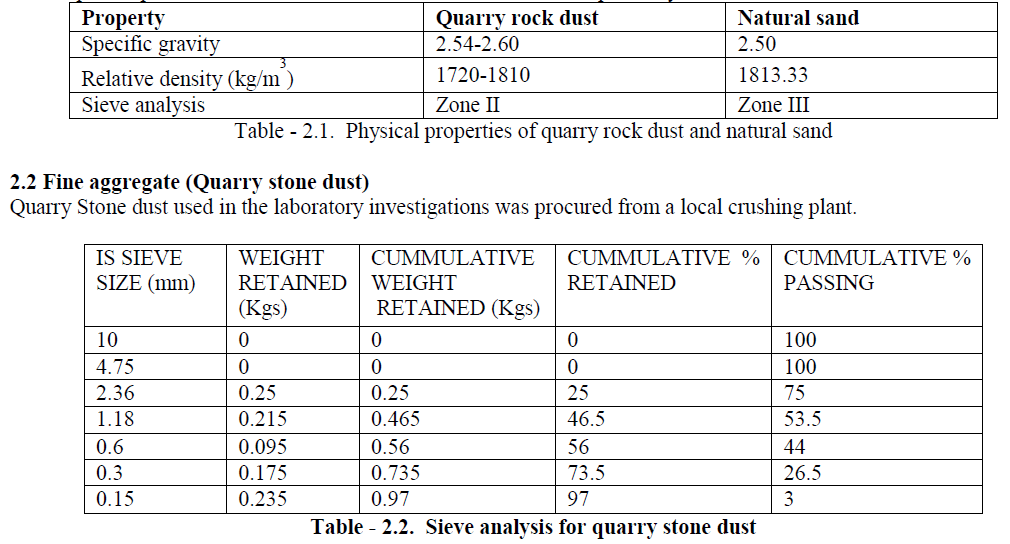
Multipliers are the basic building blocks of many VLSI computational units. The performance of such VLSI circuits depends on the performance of multipliers. Hence designing a high performance multiplier is a challenging task for VLSI designers. Wallace tree multiplier or Wallace multiplier is the most popular multiplier among the existing multipliers. Wallace multiplier is also known for its fast speed and low power consumption. Different techniques for designing a Wallace multiplier are available in the literature. In this paper, performance comparison review of various Wallace multiplier architectures is included.
Keywords |
| Wallace multiplier, Reduced complexity, Power Dissipation, Delay. |
INTRODUCTION |
| Digital signal processors are designed in such a way that it has a feature of DSP algorithm in real time. The basic
building blocks of DSP are multiplier, arithmetic logic unit and multiply and accumulate unit. For real time
applications the key issues in the design of computational building blocks of digital signal processor are speed and
accuracy [1]. Multiplication is essential for computers, process controllers, microprocessors, digital signal processing
and graphic engines. In DSP processor, multiplication is done by multiplier. So, system performance is determined by
the performance of the multiplier. Hence various multiplier architectures have been proposed to increase the
performance of the multiplier. |
| There are different factors that drive for high performance electronic system design in terms of low power dissipation
and high speed [2-3]. With the recent advances in technology, many researchers have worked on the design of
increasingly more efficient multipliers. Main aim is to offer higher speed and lower power dissipation. This makes
them compatible for various complex and portable VLSI circuit implementations. The block diagram of multiplier
architecture is shown in Fig.1. The multiplier architecture consists of three parts: generation of partial product, addition
of partial product and final addition. |
 |
| Fig.1.Block diagram of multiplier architecture |
| Parallel multipliers are the high speed multiplier. There are so many multiplier architectures that are available for
designing parallel multiplier. Wallace multiplier is one of them. A Wallace tree is an efficient hardware implementation
of a digital circuit. It can multiply two integers. A multiplier based on Wallace-tree structure is called Wallace
multiplier. It is substantially faster than other multiplier [4]. |
| In this paper, several types of Wallace multiplier architectures are studied that have reduced complexity, low power
consumption and less latency as compared to the conventional Wallace multiplier. |
RELATED WORK |
CONVENTIONAL WALLACE MULTIPLIER |
| A conventional Wallace multiplier is an efficient parallel multiplier. Wallace multiplier architecture has also three
steps. In the first step, it generates partial product. If the multiplication is of NxN bits, then it produces N2 partial
product. In accumulation of partial product, group of three adjacent rows are collected. Each group of three rows is
reduced by using full adders and half adders. Full adders are used in each column where there are three bits whereas
half adders are used in each column where there are two bits. If there is any single bit in any stage then it is passed to
the next stage without any processing. The procedure of reduction is repeated unless two rows are obtained [4]. Fig. 2
shows 9-bit conventional Wallace multiplier architecture [5]. This figure shows that the multiplication is achieved in
three steps and the number of rows in the initial bit product array is nine. |
| For an N-bit multiplier, the number of rows in the initial bit product array, r0, is N. The number of rows in subsequent
stages of a conventional Wallace multiplier can be written as [5] |
 |
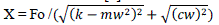 |
| Here, ri denotes the groups or stages, and ri mod 3 denotes the smallest non negative remainder of ri/3. The number of
rows in subsequent stages of a conventional 9-bit Wallace multiplier is calculated by using eqn.1. For a conventional
9-bit Wallace multiplier, r0=N=9, r1=6, r2=4, r3=3, r4=2. |
 |
| Fig.2. 9-bit Conventional Wallace multiplier |
REDUCED COMPLEXITY WALLACE MULTIPLIER |
| Waters et al. presented the reduced complexity Wallace multiplier approach. Fig. 3[5] shows a reduced complexity
Wallace multiplier. It is a modification to the second phase reduction method used in the conventional Wallace
multiplier, in which number of the half adders is reduced. In the first phase, the partial product array is formed and it is
converted in the form of an inverted pyramid array. An inverted pyramid array is formed when the bits in the left half
of the partial product array is shifted in the upward direction. In the second phase, this array is divided into group of
three rows each and full adders are used in each column. Half adders are used only when the number of reduction stages of the modified Wallace multiplier is exceeding that of the conventional Wallace multiplier. So this method
reduces the number of half adders. |
| In this modified Wallace multiplier, if (ri mod 3) = 0, then half adder is needed in the reduction stage; otherwise half
adder is not required. The number of half adders in this architecture is equal to N-S-1, where N is the number of bits,
and S is the number of stages. For 9-bit multiplication using this Wallace multiplier architecture, only one half adder is
used in the first and the second stage and two half adders are used in the final stage as shown in Fig. 3 [5]. Therefore, it
is observed that the number of the reduction stages remain the same as compared to the conventional Wallace reduction
whereas two more full adders and 17 fewer half adders are used in this modified Wallace multiplier in comparison with
the conventional Wallace multiplier. |
 |
| Table 1[5] shows the comparison of complexity between the conventional Wallace multiplier and the reduced
Wallace multiplier for sizes of 8, 16, 24, 32 and 64 bits. This table shows that using both multipliers yield the same
number of the reduction stages, but the modified or reduced complexity Wallace multiplier has the advantage of
reduced complexity in the number of gates. |
| TABLE 1: COMPARISON OF COMPLEXITY |
 |
 |
NOVEL LOW POWER AND HIGH SPEED WALLACE MULTIPLIER |
| A novel low power and high speed Wallace multiplier uses carry save addition algorithm to reduce the overall latency
[6]. This leads to increased speed and reduced power dissipation. This is accomplished by the use of compressors in
place of full adders, and the uses of Sklansky tree adder in place of the final carry propagate stage. The novel low
power and high speed Wallace multiplier for RISC processors in shown in Fig.4 [6]. In the partial product reduction
stage, if the number of adders used is decreased, it correspondingly reduces the latency in the Wallace tree multiplier.
In this multiplier, two full adders having delay of four units are replaced by a single 4:2 compressor having latency of
three units and 5:2 compressor having latency of four units replace three full adders having latency of six units. The use
of the Sklansky adder in the structure further results in a reduced latency. |
 |
| Fig.4. Novel low power and high speed Wallace multiplier |
BOOTH RECODED WALLACE TREE MULTIPLIER |
| Booth Recoded Wallace Tree Multiplier comprises of Booth recoding algorithm and compressor adders for its
realization [7]. In this architecture, Booth Recoding algorithm is introduced to generate and reduce the number of the
partial products of multiplier, whereas, 3:2, 4:2, and 5:2 compressor structures are introduced to reduce the number of
partial product addition stages. In these compressors, critical delay path is minimized by replacing the XOR blocks
with multiplexer blocks. Final two rows are summed using Carry Select Adder to produce the final result. This
architecture has the advantage of higher speed and lower area. |
EFFICIENT HIGH SPEED WALLACE TREE MULTIPLIER |
| In contrast to the conventional Wallace tree multiplier, an efficient high speed Wallace tree multiplier is composed of
compressor adders and modified carry select adder [8]. In this architecture, 4:2 and 5:2 compressors are used for partial
product reduction in the second stage whereas carry select adders are used to perform addition of two rows of bits in
the final stage for reduction in carry propagation latency of the Wallace multiplier. |
| An efficient high speed Wallace tree multiplier architecture has the advantage of reduced latency and reduced power
consumption than the conventional Wallace multiplier. Table 2 [8] shows comparison of number of transistor and
latency using 8-bit Conventional Wallace Multiplier and 8-bit Efficient High speed Wallace Tree Multiplier
architectures. This table shows that the area is also reduced by using an efficient high speed Wallace tree multiplier in
comparison with the conventional Wallace Multiplier because of the decrease in the number of transistors. |
| Table 2. Comparison of number of transistor and latency |
 |
WALLACE MULTIPLIER USING ENERGY EFFICIENT CMOS FULL ADDER |
| Fig. 5 [9] shows the block diagram of Wallace multiplier architecture using energy efficient CMOS full adder. In this
method modified reduced complexity Wallace Multiplier is designed with reduced power consumption and area by
using energy efficient CMOS full adder in place of conventional full adder [9]. This multiplier architecture reduces
power dissipation and also total number of gate counts is reduced. In this architecture, energy efficient CMOS full
adder is used in place of conventional full adder. This reduces the overall power dissipation and also increases the
speed. |
 |
| Fig.5. Wallace multiplier using Energy efficient CMOS full adder |
CONCLUSION |
| In this paper, several types of Wallace multiplier architectures are studied and compared with the conventional
Wallace multiplier architecture. It is observed that with reduced complexity and use of efficient adders, Wallace
multiplier architecture gives better performance in terms of power, delay and area. |
References |
- Wallace, C. S., “A Suggestion for a Fast Multiplier”, IEEE Transactions on Computers, vol. 13, pp. 14-17, 1964.
- Kumar, M., Hussain, M. A., and Paul, S. K., “Performance of a Two Input Nand Gate Using Subthreshold Leakage Control Techniques”,Journal of Electron Devices, Vol. 14, pp. 1161-1169, 2012.
- Kumar, M., Hussain, M. A., and Singh, L. K., “Design of a Low Power High Speed ALU in 45nm Using GDI Technique and Its PerformanceComparison”, Communications in Computer and Information Science, Springer Berlin Heidelberg, Vol. 142, pp. 458-463, 2011.
- Gandhi, D. R., and Shah, N. N., “Comparative Analysis for Hardware Circuit Architecture of Wallace Tree Multiplier”, IEEE InternationalConference on Intelligent Systems and Signal Processing, Gujarat, pp. 1-6, 2013.
- Swartzlander, E. E., and Waters, R. S., “A Reduced Complexity Wallace Multiplier Reduction”, IEEE Transactions on Computers, vol. 59, pp.1134-1137, 2010.
- Vinoth, C., Bhaaskaran, V. S. K., Brindha, B., Sakthikumaran, S., Kavinilavu, V., Bhaskar, B., Kanagasabapathy, M., and Sharath, B., “A Novel Low Power and High Speed Wallace Tree Multiplier for RISC Processor”, IEEE 3rd International Conference on Electronics ComputerTechnology, Kanyakumari, pp. 330 – 334, 2011.
- Dubey, S., and Rao, M. J., “A High Speed and Area Efficient Booth Recoded Wallace Tree Multiplier for fast Arithmetic Circuits”, IEEE AsiaPacific Conference on Postgraduate Research in Microelectronics & Electronics, Hyderabad, pp. 220 – 223, 2012.
- Sureka, N., Porselvi, R., and Kumuthapriya, K., “An Efficient High Speed Wallace Tree Multiplier”, IEEE International Conference onInformation Communication and Embedded system, Chennai, pp. 1023-1026, 2013.
- Khan, S., Kakde, S., and Suryawanshi, Y., “VLSI Implementation of Reduced Complexity Wallace Multiplier Using Energy Efficient CMOSFull Adder”, IEEE International Conference on Computational Intelligence and Computing Research, Coimbatore, pp. 1-4, 2013.
|