Keywords
|
| 5022-U. 427 G-AG Orange, 427 G-AG Green and Super-10, Polynomial equation, Average precipitation rate |
INTRODUCTION
|
| The water is precious and limited resource that is essential for agricultural production, which must be conserved and used judiciously. India is huge country with very large agricultural base, but the water resources in India are very limited. The main objective of irrigation is to apply the optimum amount of water to the crop root zone that the crop needs for development and also that cannot be provided by rains [7]. An ideal irrigation system should minimize the losses, and apply the water uniformly [2]. In the sprinkler method of irrigation, water is sprayed into the air and allowed to fall on the ground surface somewhat resembling rainfall. The spray is developed by the flow of water under pressure through small orifices or nozzles. The use of mini sprinkler provides low adjusted discharge with high uniformity of application. Irrigation with mini sprinklers in many close growing crops and orchards indicated a yield and water saving over conventional method. In mini sprinkler irrigation methods water is spread into the air and allowed to fall on ground surface as rainfall. The spray is developed by the flow of water flowing under pressure through small openings. The basic objective of mini sprinkler is to simulate rainfall and to apply uniform water to crop. The mini sprinkler protect crop against high temperature and frost that reduces quality and quantity of harvest. So, this method is becoming popular in the region of water scarcity where available water is insufficient to irrigate the command area by surface irrigation methods. There are many applications of mini sprinkler such as under foliage irrigation, wetting of foliage, especially suitable for light, sandy soil, Recommended for the irrigation of open field crops like potato, leafy vegetables, cotton, oil seeds, pulses, cereals, etc. The performance of sprinkler irrigation is judged by its uniformity of distribution of water which depends on the proper, efficient and economic design of the system. For this it is important to keep initial equipment cost and operation cost as low as possible to ensure the better quality product with the highest returns from the investment made. But adequate attention has not been paid to the hydraulic characteristics of different components of the system and the effect of different variables such as operating pressure, nozzle size etc. This affects the distribution pattern and the economy to great extent [3]. The aim of the study reported here was to investigate pressure-discharge, pressure-radius of throw and pressure- average precipitation rate of single mini-sprinkler head relationships. The discharge and diameter of throw increases with increase in pressure for all types of micro-sprinklers [6, 1]. |
II. MATERIAL AND METHODS
|
| 2.1 Experimental site An experiment was conducted on the experiment farm of College of Agricultural Engineering and Technology, M. K. V., Parbhani. 2.2 Experimental setup For hydraulic studies of mini sprinkler irrigation system separate experimental setup was made in open field. Objective of such study was to optimize the design variables such as nozzle size, operating pressure, radius of influence, discharge of sprinkler for different conditions etc. Experimental setup consisted of pump(5 HP), main (PVC pipe of class II 90 mm diameter)and submain pipe(PVC pipe of class II 63 mm diameter), filters(sand filter of capacity 25 m3 / hr and screen filter of 25 m3 / hr), laterals(JISL -IS- 12786 class II of 25 mm diameter), risers, sprinkler head, pressure gauge. Under this set-up four makes of mini-sprinkler were evaluated in this study. A twin nozzle 5022 U (yellow + green) and three single nozzle mini-sprinklers 427 G-AG (orange), 427 G-AG (green), and Super 10 (blue) respectively, used to study their performance on field. All those were manufactured by Jain Irrigation Systems Ltd., Jalgaon. |
 |
| 2.2 Measurement of discharge The experiment was conducted at five different operating pressures of 2.0, 2.5, 3.0, 3.5 and 4.0 kg/cm2. The required operating pressure at the nozzle was adjusted by the valve and bypass arrangement. To measure the discharge from the nozzle at sprinkler position, 1.27 cm inner diameter rubber tube was fixed at one end of 5022 U (twin nozzle) and its other end was put in the plastic bucket of 20 liter capacity. For remaining three single nozzle mini-sprinkles, discharge was measured by dipping the nozzle into the bucket. Time taken to fill the bucket was 1 minute noted by stop watch for each combination and the observations were replicated thrice to get accuracy in results. The water collected in bucket was measured with the help of graduated cylinder and then converted in discharge per hour. 2.3 Measurement of radius of throw The wetted radius of throw for each mini-sprinkler was measured at different pressures ranging from 2.0 to 4.0 kg/cm2 with an increment of 0.5 kg/cm2 by gradually increasing the pressure. It was measured directly by the measuring tape from the centre of the sprinkler head to the end of water throw. |
| 2.4 Pressure – discharge – radius of throw relationship The mathematical relationships (linear, logarithmic, power, polynomial and exponential) between pressure – discharge and pressure – radius of throw were developed from observation data on pressure, discharge and radius of throw. The best-fit equation was decided on the basis of regression coefficient (r2). The value of r2 of polynomial equation was higher than those of linear, logarithmic, power and exponential. Due to this fact, the polynomial equation was considered for plotting the curves. |
| 2.5 Precipitation rate The precipitation rate is the speed at which a sprinkler or an irrigation system applies the water. To determine the precipitation rate, four mini-sprinkler nozzles were operated at pressures of 2.0, 2.5, 3.0, 3.5 and 4.0 kg/cm2. The volume of precipitation collected in cans was measured with the help of graduated cylinder. The precipitation rate was measured by following equation [3]. |
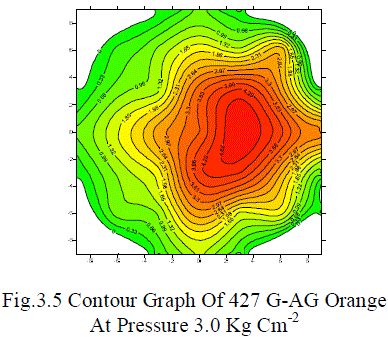
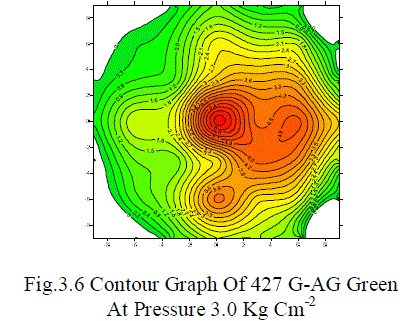
| 2.6 Distribution pattern To determine the water distribution pattern in mini-sprinkler irrigation method, the tests were conducted for single sprinkler head. For single mini-sprinkler head pattern, the precipitation depth in catch cans placed at grid of 3 x 3 m spacing for 5022-U, 427 G-AG Orange and 427 G-AG Green nozzles and 2 x 2 m spacing for Super 10 nozzle were measured. The average depth of water collected at each sampling point was calculated. The observed depths of water in each test were used to draw contours using software Surfer v.8.0 for water depth distribution. These contours will show the distribution pattern of water application for particular test. |
III. RESULTS AND DISCUSSION
|
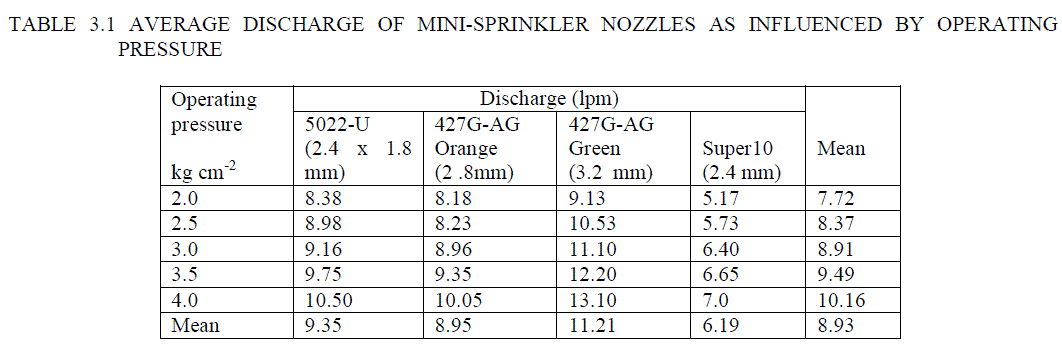
| 3.1 Pressure – discharge relationship The average discharges for all types of mini-sprinkler nozzles are reported in Table 3.1. The graphical presentation of pressure to discharge relationship is depicted in Fig. 3.1. The table gives average values of three observations. From Table 3.1 it is revealed that the minimum discharge of 5.17 lpm was observed for Super 10 nozzle at operating pressure of 2.0 kg cm-2. The maximum discharge of 13.10 lpm was observed for 427 G-AG Green nozzle at operating pressure of 4.0 kg cm-2. Data presented in Table 3.1 shows the minimum discharges were observed at operating pressure of 2.0 kg cm-2 and the maximum discharges were observed at operating pressure of 4.0 kg cm-2. This reveals that the discharge of nozzle increases with increase in operating pressure. The data follows the well established principle and findings [4]. |
 |
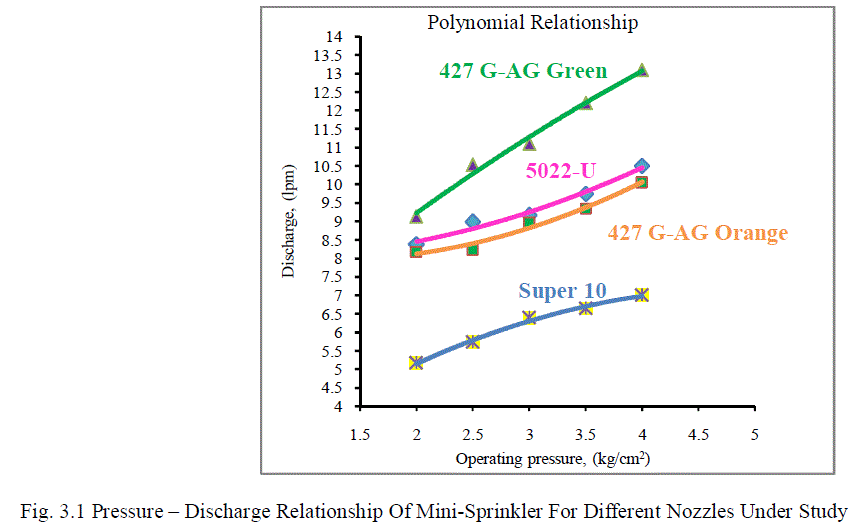 |
| The relationship between the operating pressure and discharge under all four mini-sprinklers were developed in the form of linear, logarithmic, power, polynomial and exponential. The best fit relationship between the operating pressure head (H) and discharge (Q) of mini-sprinkler was determined in the form of following polynomial equations. Nozzle Relationship Regression coefficient 5022-U Q = 0.202H2 - 0.215H + 8.072 r2 = 0.980 ----3.1 427G-AG Orange Q = 0.274H2 - 0.673H + 8.369 r2 = 0.978 ----3.2 427 G-AG Green Q = -0.134H2 + 2.727H + 4.304 r2 = 0.989 ----3.3 Super 10 Q = -0.24H2 + 2.356H + 1.402 r2 = 0.992 ----3.4 |
| Q = Discharge |
| H = Operating pressure |
| Usually the relationship between the operating pressure and discharge is in the form of power relationship (Vermerien and Jobling 1980). The r2 values found in power relationship are 0.95, 0.91, 0.99 and 0.99 for 5022-U, 427 G-AG Orange, 427 G-AG Green and Super 10, respectively. The polynomial relationship was also found to be better in the present investigation with r2 values of 0.98, 0.98, 0.99 and 0.99 respectively which may be due to limited range of operating pressure (2.0 to 4.0 kg cm-2) in the present investigation. However there was no significant difference between r2 values of power and polynomial relationship. Hence the polynomial relationship was considered to be the best fit (equation 3.1, 3.2, 3.3 and 3.4). Statistical analysis showed that the mean discharge obtained at 4 kg cm-2 operating pressure is found to be maximum as 10.16 lpm and significantly superior over all other operating pressures. Data also indicate that as the operating pressure increases from 2.0 to 4.0 kg cm-2, mean discharge increases from 7.12 to 10.16 lpm. The interaction effect of pressure v/s nozzle size is found to be significant. Among the nozzles tested, the 427 G-AG Green nozzle produced maximum discharge i.e. 11.21 lpm as compared to all nozzles and found significantly superior. |
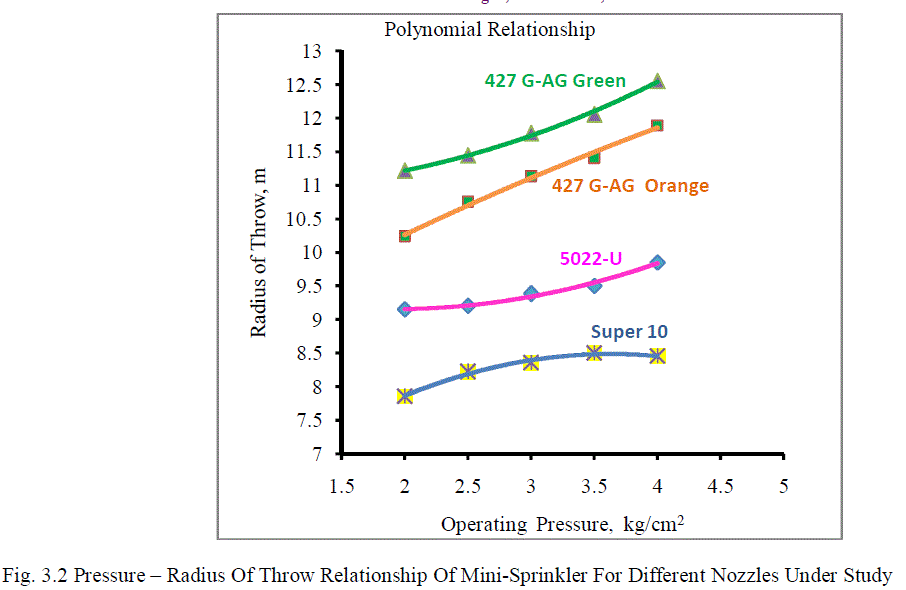
| The observations of radius of throw of four different mini-sprinkler nozzles (5022-U, 427 G-AG Orange, 427 G-AG Green and Super 10) were recorded for different operating pressures ranging from 2.0 to 4.0 kg cm-2 with an increment of 0.5 kg cm-2. The average radius of throw for all types of mini-sprinkler nozzles is reported in Table 3.2. The graphical presentation of pressure to radius of throw relationship is depicted in Fig. 3.2. The table gives average values of three observations. |
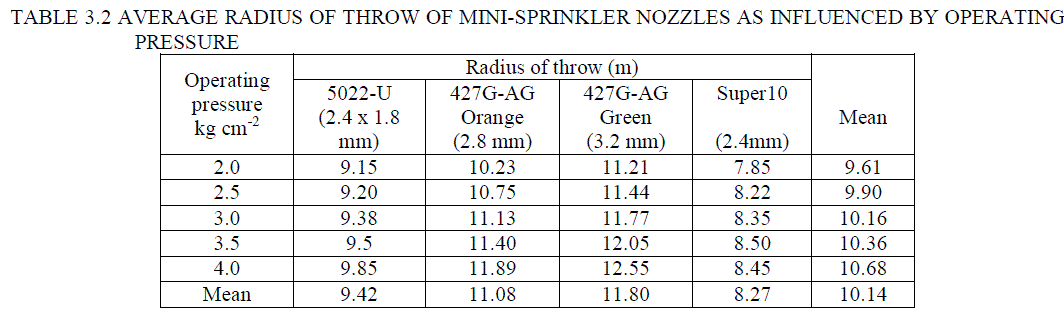 |
| From Table 3.2 it is observed that as the operating pressure increases from 2.0 to 4.0 kg cm-2, the radius of throw increases from 9.15 to 9.85 m, 10.23 to 11.89 m, 11.21 to 12.55 m and 7.85 to 8.45 m for 5022-U, 427 G-AG Orange, 427 G-AG Green and Super 10, respectively. It is also revealed that minimum radius of throw of 7.85 m was observed for Super 10 nozzle at operating pressure of 2.0 kg cm-2 and maximum radius of throw of 12.55 m was observed for 427 G-AG Green nozzle at operating pressure of 4.0 kg cm-2. It was also revealed that the increase in operating pressure increased the radius of throw of all mini-sprinkler nozzles. For all types of mini-sprinkler nozzles, pressure – radius of throw relationships were established in the form of linear, logarithmic, power, polynomial and exponential. The best fit relationship between the operating pressure head (H) and radius of throw (R) of mini-sprinkler was determined in the form of following polynomial equations. |
 |
| Nozzle Relationship Regression coefficient 5022-U R = 0.154H2 - 0.585H + 9.707 r2 = 0.986 ----3.5 427G-AG Orange R = 0.274H2 - 0.673H + 8.369 r2 = 0.991 ----3.6 427 G-AG Green R = -0.048H2 + 1.085H + 8.285 r2 = 0.996 ----3.7 Super 10 R = -0.234H2 + 1.701H + 5.394 r2 = 0.987 ----3.8 |
| R = Radius of throw |
| Statistical analysis showed that the mean radius of throw obtained at 4 kg cm-2 operating pressure is found to be maximum as 10.68 m and significantly superior over all other operating pressures. Data also indicate that as the operating pressure increases from 2.0 to 4.0 kg cm-2, mean radius of throw increases from 9.61 to 10.68 m. The interaction effect of pressure v/s nozzle size is found to be significant. Among the nozzles tested, the 427 G-AG Green nozzle produced maximum radius of throw i.e. 11.80 as compared to all nozzles and found significantly superior. |
| 3.3 Precipitation rate of single mini-sprinkler head |
| The precipitation volume of 5022-U, 427 G-AG Orange and 427 G-AG Green nozzles were collected in catch cans placed at each grid spacing of 3 x 3 m and for Super 10 nozzle it was collected at each grid spacing of 2 x 2 m. The volume of water collected then converted into depth of precipitation. The precipitation rate of four nozzles was estimated at different operating pressures ranging from 2.0 to 4.0 kg cm-2 with an increment of 0.5 kg cm-2. The average precipitation rates of nozzles influenced by different operating pressure are reported in Table 3.3. |
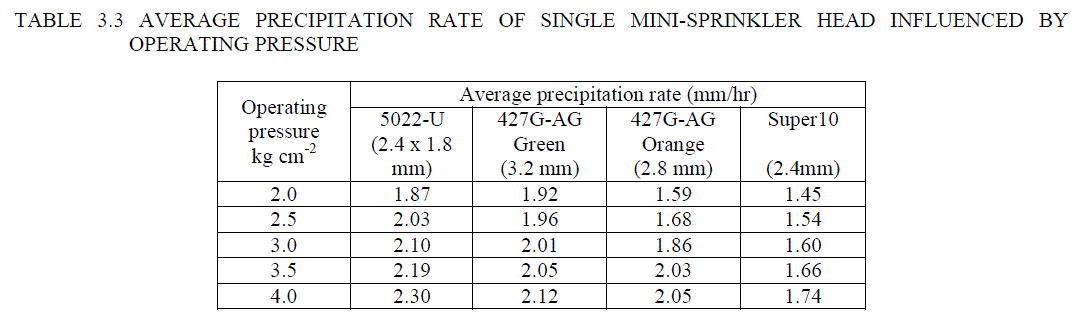 |
| Data presented in Table 3.3 show that the minimum precipitation rate of 1.45 mm hr-1 was observed for Super 10 nozzle at operating pressure of 2.0 kg cm-2 and maximum precipitation rate of 2.30 mm hr-1 was observed for 5022-U nozzle at operating pressure of 4.0 kg cm-2. Data in Table 3.3 reveal that as the operating pressure increases from 2.0 to 4.0 kg cm-2, the average precipitation rate of single mini-sprinkler head increases for all nozzles. It is also seen that as the nozzle size increases the precipitation rate increases. |
| 3.4 Distribution pattern of single mini-sprinkler head |
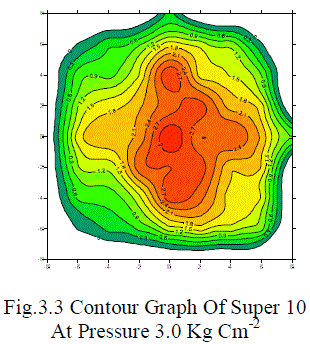
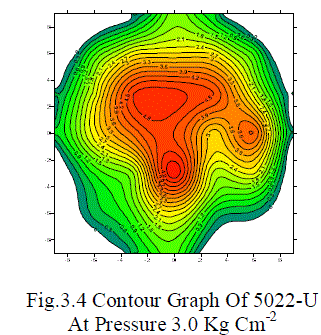
| The effect of operating pressure on distribution pattern of single mini-sprinkler head for all nozzles is depicted in Fig.3.3, 3.4, 3.5, 3.6 From the contours, it is observed that 3 kg cm-2 operating pressure gives more uniform distribution as compared to all other operating pressures. The effect of wind velocity is also seen on all distribution patterns. |
 |
 |
 |
 |
References
|
- AA. Kale, Hydraulic performance of pop-up sprinkler irrigation. Unpublished B. Tech. (Agril. Engg.) thesis submitted to M. A. U., Parbhani, 2006.
- D.Z. Haman, A.G. Smajstrla, and D. J. Pitts, Uniformity of Sprinkler and Microirrigation Systems for Nurseries.Florida Cooperative Extension Service University of Florida, BUL321, 2003.
- Hunter, Users guide. Hunter industries incorporated, California, 17, 2006.
- Vermerein, and C. A. Jobling , Localized irrigation. Irrigation and Drainage paper, F. A. O., Rome, 34-22, 2004.
- S. B. Jadhav, R. G. Bhagyawant, U. M. Khodake and D. V. Raut 2009. Distribution pattern of pop-up sprinkler under different operating condition. International Journal of Agricultural Engineering, 2 (1): 9-13.
- S. L. Muley, Hydraulic performance of micro-sprinkler irrigation. Unpublished B. Tech. (Agril. Engg.) Thesis submitted to M. A. U., Parbhani, 2004.
- T. Kara, E. Ekmekci, and M. Apan, Determining the uniformity coefficient and water distribution characteristics of some sprinklers. Pakistan Journal of Biological Sciences 11(2):214-219, 2008.
|