ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| .M.Kannan1, P.K.Arun Kumar2, M.Poomanirajan3 Department of Electrical and Electronics Engineering, K.L.N. College of Engineering, Madurai, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Frequency deviations and inter-area tie-line power fluctuations by a local load disturbance are a source of interconnected power system operation and control. This paper describes the application of artificial neural network (ANN) based Adaptive Neuro-Fuzzy Inference system (ANFIS) for automatic generation control (AGC) of a three area hydro-thermal system. The proposed technique combines the advantages of fuzzy logic controller and adaptability nature of ANN. The objective of design is to improve the AGC performance by damping the frequency deviations and tie-line power fluctuations in the interconnected power system. Simulation result shows the comparison of Integral controller, Fuzzy logic controller (FLC) and ANFIS controller. The results indicate that ANFIS controller exhibits better performance than other controllers.
Keywords |
| Automatic Generation control, Integral Controller, Fuzzy Logic Controller, Adaptive Neuro-Fuzzy Inference System. |
INTRODUCTION |
| Automatic generation control (AGC) is a vital process of modern interconnected power systems. A well designed AGC system is capable of not only assisting electrical energy quality, but also of achieving substantial economic benefits. The AGC and its relevant studies include response characteristic research, control strategy design, control criteria developing, etc. A fast, accurate and user-friendly simulation system is required for these studies[1]. An interconnected power system has several areas and for the stable operation of power systems; both constant frequency and constant tie-line power exchange should be provided. In each area, an AGC monitor the system frequency and tie-line flows, compute the net change in the required generation (generally referred to as Area Control Error – ACE) and changes the set position of the generators within the area so as to keep the time average of the ACE at a low value[2]. Therefore ACE, which is defined as a linear combination of power net-interchange and frequency deviations, is generally taken as the output of AGC. As the ACE is drive to zero by the AGC, both frequency and tie-line power error will be forced to zeros[3]. AGC function can be viewed as a supervisory control function which attempts to match the generation trend within an area to the trend of the arbitrarily changing load of the area, so as to keep the frequency and the tie-line power flow close to listed value. The growth in size and complication of electric power systems along with increase in power demand has necessitated the use of intelligent systems that combines knowledge, techniques and methodologies from various sources for the real-time control of power systems[4-6]. The researchers in the world over trying to understand several strategies for AGC of power systems in order to keep the system frequency and tie line flow on their listed values during normal operation and also during small perturbations[7]. In this work AGC simulation study has been carried out to show the effect of ANFIS based controller in damping oscillations for transient responses in hydro-thermal three area system. The transient responses obtained using conventional integral controller has been further improved by replacing the integral controller with fuzzy controller and then with ANFIS[8,9]. Literature survey shows that small attention has been given to the study of AGC of multi-area systems. And, in these studies of multi-area systems, the focus has been to optimize the supplementary controller gains using artificial neural network (ANN), hybrid genetic algorithm-simulated annealing (GA-SA) or fuzzy logic based techniques. Various heuristic search approaches such as genetic algorithm (GA), optimal, and particle swarm for optimizing the controllers is available in the literature. Also, They have demonstrated that bacterial foraging, a further recent and powerful evolutionary computational technique, based PI controller provides better performance as compared to that with integral controller based on classical and GA techniques in three areas thermal system. There has also been considerable research work attempting to propose better AGC systems based on modern control theory, neural network, fuzzy system theory and reinforcement learning. Recent studies show that ANFIS approach has also been applied to hydrothermal system. All research in the past in the area of AGC pertains to interconnected two equal area thermal system and little attention has been paid to AGC of unequal multi area systems[10-14]. |
| Most of past works have been centered around the design of governor secondary controllers, and design of governor primary control loop. Apparently no literature has discussed AGC performance subject to simultaneous small step load perturbations in all area or the application of ANFIS technique to a multi-area power system. It is a maiden application of ANFIS approach to a three area hydrothermal system considering small step load perturbation occurring in all the areas |
II. TEST SYSTEM |
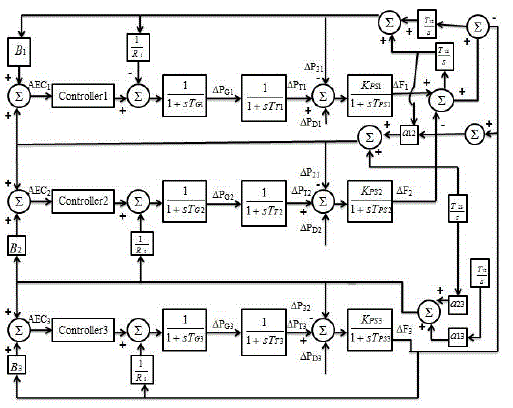
| The AGC system considered is consists of three generating areas of equal sizes. Areas 1 and 2 are hydro systems and area 3 is a thermal system. The characteristics of hydro turbine differ from steam turbine in many respects. The typical value of permissible rate of generation for hydro plant is relatively much higher (a typical value of generation rate constraints (GRC) being 270%/min for raising generation and 360%/min for lowering generation), as compared to that in favor of reheat type thermal units having GRC of the order of 3%/min. Fig.1 shows the AGC model of a three area system. The thermal plant has a single stage reheat steam turbine and the hydro plant is prepared with an electric governor. A bias setting of Bi = βi is considered in both hydro and thermal areas. MATLAB version 8.1 has been used, to obtain dynamic responses for frequency and tie-line power deviations for 1% step load perturbation in all Fig.1 AGC model of three area system |
| areas. The proportional integral derivative controller (PID) is the most popular feedback controller used in the process industries. Whereas proportional and integrative modes are often used as single control modes, a derivative mode is not often used as it amplifies the signal blare. In view of the above, a PI structured controller is considering in the present paper. The propose of PI controller requires determination of the two parameters, Proportional gain (KP) and Integral gain (KI) by Ziegler – Nicholas method. The controllers in both the areas are considered to be identical so that KP1=KP2=KP3=K and KI1=KI2=KI3=K. The system parameters are given in Appendix A. |
III. FUZZY LOGIC CONTROLLER |
| It mainly consists of four principal components as fuzzification inference, knowledge base (rule base and data base), decision making unit and defuzzification inference. It is normally a two-input and single-output system i.e. a MISO system. Fuzzification Inference: The crisp domain is mapped into the fuzzy domain. It transforms the input data into linguistic values. Fuzzy Sets: Membership functions are the characteristic representation of fuzzy sets. These may be the bell shaped, triangular function, linear function, trapezoidal function and exponential function. Knowledge Base: The knowledge of application domain and attendant control goals is comprised in the form of sets of linguistic control rules. Inference Engine: The operating conditions from the measured values are determined. The appropriate control action is selected by using the rule base which is created from the expert system knowledge. Defuzzification Inference: The range of the values corresponding to output variables is decided by scale mapping. The inferred decision from the linguistic variables is converted back to the numerical values. |
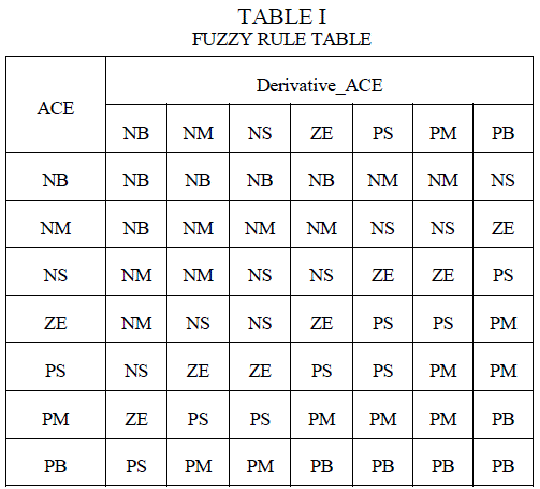
| Membership Function: Membership function defines the fuzziness in a fuzzy set irrespective of the elements in the set, which are discrete or continuous. Membership function can be thought of as a technique to solve empirical problems on the basis of experience rather than knowledge. A linear triangular membership functions are used for both input and output variables. A set of rules which define the relation between the inputs and output of fuzzy controller are defined using the linguistic variables. The understanding required to generate the fuzzy rules can be obtained from an offline simulation. Though, it has been noticed that, for monotonic systems, a symmetrical rule table is very suitable, although sometimes it may need slight adjustment based on the behavior of the specific system. If the system dynamics are not identified or are highly nonlinear, trial-and-error events and experience play an important role in framing the rules. In the proposed rules, the input variables are connected by an âÃâ¬Ãâ¢ANDâÃâ¬Ãâ method and it is meant that membership degree of a ACE is the minimum value among the membership degree of the input variables. For the proposed AGC, 49 rules are defined and they are shown in Table.1. The linguistic variables are NB – Negative Big, NM – Negative Medium, NS – Negative Small, ZE – Zero, PS – Positive Small, PM – Positive Medium, PB – Positive Big. |
 |
 |
IV.ADAPTIVE NEURO-FUZZY INFERENCE SYSTEM |
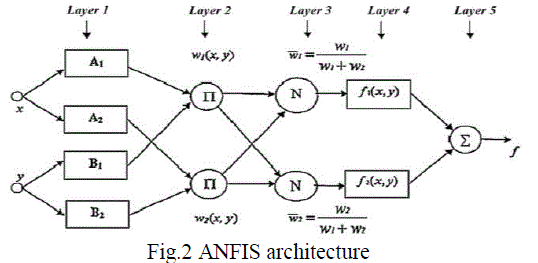
| ANFIS is resembles to be an adaptive network, which is very alike to neural networks. It has no synaptic weights, but has so called adaptive and non-adaptive nodes. It have to be said that adaptive network can be easily transformed to neural network architecture with classical feed forward topology. ANFIS is adaptive network which works like adaptive network simulator of Takagi–Sugeno’s fuzzy controllers. This adaptive network is functionally the same to a fuzzy inference system (FIS). Using a given input/output data set, ANFIS adjusts all the parameters using back propagation gradient descent and least squares type of method for non-linear and linear parameters respectively. It is assumed for easiness that the fuzzy inference system under concern has two inputs x and y and one output z. Suppose that the rule base contains two fuzzy if-then rules of Takagi and Sugeno’s type. The given concept of ANFIS structure can be explained using a simple example whose rule base is given below, |
| Rule 1 : If x is A1 and y is B1. Then f1 = p1x + q1y + r1 |
| Rule 2 : If x is A2 and y is B2. Then f2 = p2x + q2y + r2 |
| The equivalent ANFIS architecture is shown in fig.2. The three layer Multi-Layer Perceptron (MLP) structure model of ANN is applied for AGC of three area hydrothermal system. This |
| structure of ANN has an input layer, an output layer, and a hidden layer. |
 |
| Research has proved that ANNs has a extensive number of applications in the power engineering due to many advantages. In this article, ANFIS controller in MATLAB/Simulink, which is an advance adaptive control configuration of ANN, is used because the controller provides faster control than the compared PI controller. The proposed ANN controller uses back propagation through-time algorithm. The backpropagation technique is an iterative method employing the gradient decent algorithm for minimizing the square error between the actual output and the target for each and every pattern in the training. In this article, we present a data from training set with fuzzy inputs and fuzzy desired output vectors. Then revise the network weights in a recursive algorithm starting from the output layer and working backward to the first hidden layer. The learning procedure of ANFIS system takes the semantically properties of the underlying fuzzy system into account. This results in limitations on the possible modifications applicable to the system parameters. The ANFIS system consists of the components of a conventional fuzzy system except that computations at each stage is performed by a layer of hidden neurons and the neural network’s learning capacity is provided to enhance the system knowledge. |
| The proposed ANFIS controller utilizes Sugenotype fuzzy inference system (FIS) controller, with the parameters within the FIS decided by the NN back propagation method. If input–output data is observed for the system, the components of a fuzzy system (membership and consequent models) can be represented in a parametric form and the parameters can be tuned by neural networks. In that event the fuzzy systems turn into neuro-fuzzy system. The ANFIS controller is designed by taking ACE and its derivative (d(ACE)/dt) as the inputs. The output stabilizing signal is computed using the fuzzy membership functions depending on these variables. The efficiency of the proposed approach to modeling and simulation of AGC is implemented in Simulink environment of MATLAB. ANFIS-Editor is used for realizing the system and its implementation. |
| The fuzzy controller is formed with 49 rules and 7 membership functions in each variable to compute output and exhibits good performance. Now main aim is to take out a smaller set of rules using neuro-fuzzy learning and to do the same the following steps are followed: 1. Data generation: to design the ANFIS controller, some data is required, i.e., a set of two-dimensional input vectors and the associated set of one-dimensional output vectors are required. Here, the training data has been generated by sampling input variables ACE and its derivative (d(ACE)/dt) uniformly and computing the value of stabilized signal for each sampled point. 2. Rule extraction and membership functions: after generating the data, the next step is to approximate the initial rules. Then applying subtractive clustering algorithm, rules are extracted. These rules are not so close to the identified system. Hence, there is a need of optimization of these rules. Hybrid learning algorithm is used for training to modify the above parameters after obtaining the fuzzy inference system from subtracting clustering. This algorithm iteratively studies the parameter of the premise membership functions via back propagation and optimizes the parameters of the consequent equations. The training is continued until the error measure becomes constant. |
| 3. Results: The neuro-fuzzy learning has been tested on a variety of linear and nonlinear processes. The objective here is to validate whether the ANFIS controller can provide the same level of performance as that of the original one (system with 49 rules). The basic steps trailed for designing the ANFIS controller in MATLAB/Simulink is outlined: 1. Draw the Simulink model with fuzzy controller and simulate it with the given rule base. 2. The first step for designing the ANFIS controller is collecting the training data while simulating the model with fuzzy controller. 3. The two inputs, i.e., ACE and d(ACE)/dt and the output signal gives the training data. 4. Use anfisedit to create the ANFIS .fis file. 5. Load the training data collected in Step 2 and generate the FIS with trim MF’s. 6. Train the collected data with generated FIS up to a particular no. of Epochs. 7. Save the FIS. This FIS file is the neuro-fuzzy enhanced ANFIS file. |
V.RESULTS AND DISCUSSIONS |
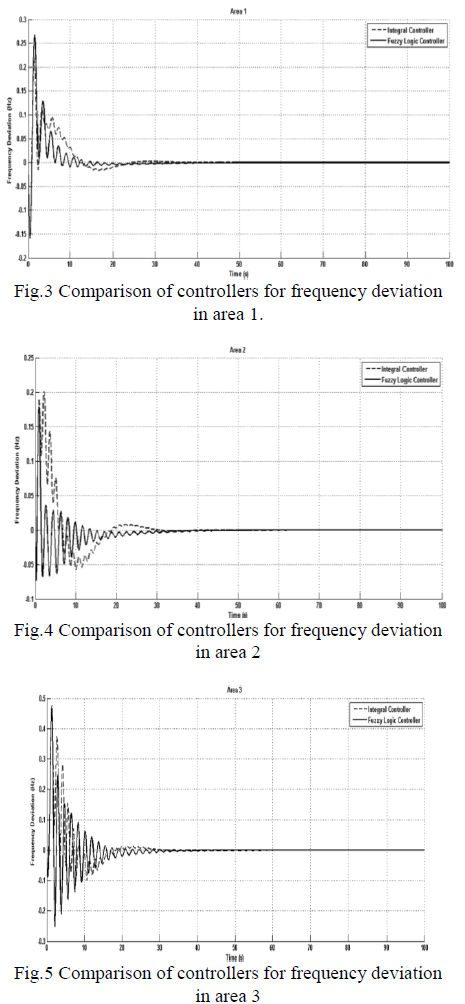
| The Model derived is simulated in MATLAB 8.1(2013a). In a multi-area system the perturbation can occur anywhere in the system, either in an area or in few areas or in all areas simultaneously. Here 1% step load perturbation is considered in all areas. Fig.3 to fig.5 shows the comparison of PI controller and fuzzy logic controller for frequenc y deviation in all three areas. |
 |
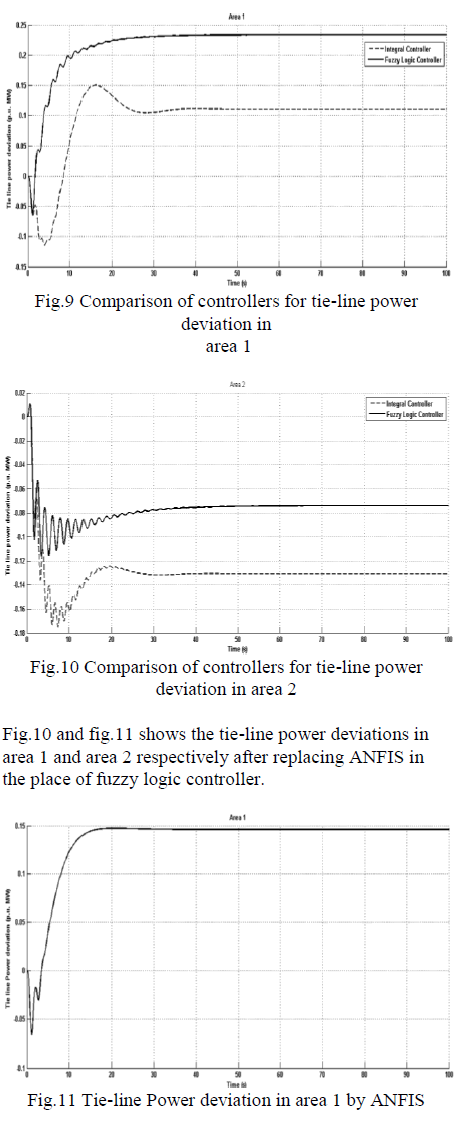
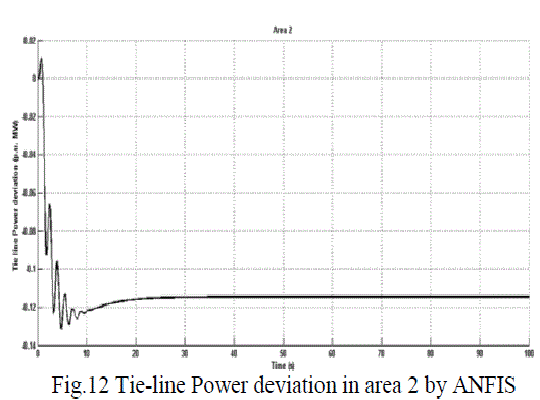
| Fig.5 to fig.7 shows the frequency deviation in three areas after incorporating ANFIS in the place of fuzzy logic controller, which damps out the oscillations further than the other mentioned controllers. |
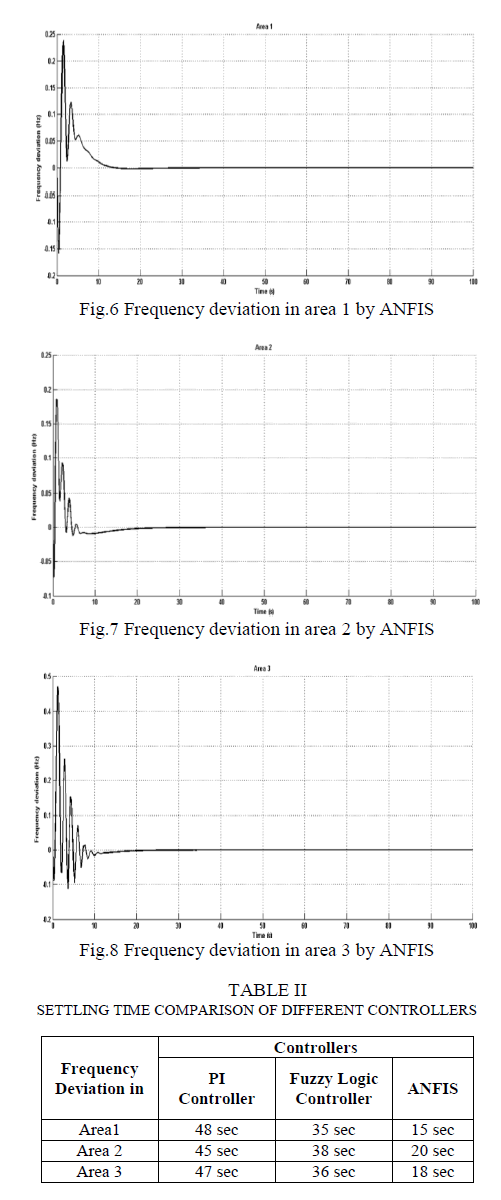 |
| Settling time comparison for three different controllers are shown in table II, which indicates that ANFIS has better performance. Tie-line power deviation comparisons for two controllers are shown in fig.5 and fig.6 for area 1 and area 2 respectively. |
 |
 |
VI. CONCLUSIONS |
| This study is an application of ANFIS controller to automatic generation control of a three unequal area hydrothermal system. The dynamic system responses have been examined considering a 1% step load perturbation in either or simultaneous areas. The conventional controller has its limitations on the part of being slow and handling nonlinearities. Since high frequency deviation may lead to system collapse, this necessitate an accurate and fast acting controller to maintain the constant nominal system frequency. The research work is intended to find the most suitable configurations of the ANFIS controller for automatic generation control of a multi-area power system. The superiority of ANFIS controller is evident from the simulation results for all types of perturbation location. Moreover, it is observed that ANFIS controller is found to be more suitable in present day power system where complexity is gradually increasing day by day. The controller design method is illustrated in a very simple and systematic manner and the efficiency of the proposed method is demonstrated through computer simulations. |
| APPENDIX A |
 |
ACKNOW LEDGMENT |
| The authors are grateful to the Principal and Management of K.L.N. College of Engineering, Madurai for providing all facilities for the research work. |
References |
|