ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
P. Ramji Thileeban1, P. Suganya2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Due to its clean and renewable nature, wind energy is becoming one of the important renewable sources of energy in the world. Through its collaboration with other renewable sources of energy, such as solar energy, the world energy crises can be solved in the future. Comparatively with the past and due to the progressive integration of the nonlinear loads in the grid, the principal role of a Wind Energy Conversion System (WECS) is not only to capture the maximum power from the wind, but also to improve the quality of power. Consequently, with the development of the wind farms which are integrated into the grid, power quality could be better improved in the future. Variable speed wind generators are frequently used and are more attractive than fixedspeed systems because of their efficient energy production, improved power quality and dynamic performance during grid faults. Recently, the most of the wind energy conversion systems are equipped with a variable speed Doubly Fed Induction Generator. Many works are done about power generation and power quality improvement using a WECS. In this paper, Bacterial foraging optimization algorithm (BFOA) is used which has been widely accepted as a global optimization. BFOA is inspired by the foraging behaviour of Escherichia coli. BFOA has drawn the attention of researchers because of its efficiency in solving real-world optimization problems arising in several application domains. It is used to obtain tuned proportional gain and integral gain, so that the power quality can be improved..
Keywords |
| Wind Energy Conversion System, Doubly Fed Induction Generator and Bacterial foraging optimization algorithm. |
INTRODUCTION |
| A WECS is a structure that transforms the kinetic energy of the incoming air stream into electrical energy |
| In order to meet power needs, taking into account economical and environmental factors, wind energy conversion is gradually gaining interest as a suitable source of renewable energy. The electromagnetic conversion is usually achieved by induction machines or synchronous and permanent magnet generators. Squirrel cage induction generators are widely used because of their lower cost, reliability, construction and simplicity of maintenance. But when it is directly connected to a power network, which imposes the frequency, the speed must be set to a constant value by a mechanical device on the wind turbine. Then, for a high value of wind speed, the totality of the theoretical power can not be extracted. To overcome this problem, a converter, which must be dimensioned for the totality of the power exchanged, can be placed between the stator and the network. In order to enable variable speed operations with a lower rated power converter, doubly-fed induction generator (DFIG) can be used. The stator is directly connected to the grid and the rotor is fed to magnetize the machine. Additionally the bacterial foraging optimization algorithm supports this project of power quality improvement in wind energy conversion system. It is a newly existed algorithm which provides the required value to the PI controller which plays a major role in this paper. |
II. DOUBLY FED INDUCTION GENERATOR |
| The DFIG is an induction machine with a wound rotor where the rotor and stator are both connected to electrical sources, hence the term ‘doubly-fed’. The rotor has three phase windings which are energized with threephase currents. These rotor currents establish the rotor magnetic field. The rotor magnetic field interacts with the stator magnetic field to develop torque. The magnitude of the torque depends on the strength of the two fields (the stator field and the rotor field) and the angular displacement between the two fields. Mathematically, the torque is the vector product of the stator and rotor fields. |
| Conceptually, the torque is developed by magnetic attraction between magnet poles of opposite polarity where, in this case, each of the rotor and stator magnetic fields establish a pair of magnet poles. Clearly, optimum torque is developed when the two vectors are normal to each other. If the stator winding is fed from a 3-phase balanced source the stator flux will have a constant magnitude and will rotate at the synchronous speed. |
III. BACTERIA FORAGING OPTIMIZATION ALGORITHM |
| During foraging of the real bacteria, locomotion is achieved by a set of tensile flagella. Flagella help an E.coli bacterium to tumble or swim, which are two basic operations performed by a bacterium at the time of foraging. When they rotate the flagella in the clockwise direction, each flagellum pulls on the cell. That results in the moving of flagella independently and finally the bacterium tumbles with lesser number of tumbling whereas in a harmful place it tumbles frequently to find a nutrient gradient. Moving the flagella in the counter clockwise direction helps the bacterium to swim at a very fast rate. In the above-mentioned algorithm the bacteria undergoes chemotaxis, where they like to move towards a nutrient gradient and avoid noxious environment. Generally the bacteria move for a longer distance in a friendly environment. Figure 1 depicts how clockwise and counter clockwise movement of a bacterium take place in a nutrient solution. |
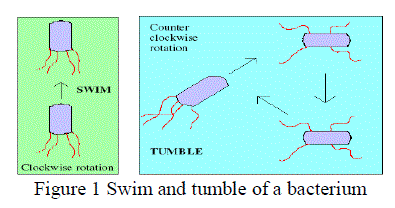 |
| When they get food in sufficient, they are increasing in length and in the presence of suitable temperature they break in the middle to from an exact replica of itself. This phenomenon inspired Passino to introduce an event of reproduction in BFOA. Due to the occurrence of sudden environmental changes or an attack, the chemotactic progress may be destroyed and a group of bacteria may move to some other places or some other may be introduced in the swarm of concern. This constitutes the event of elimination-dispersal in the real bacterial population, where all the bacteria in a region are killed or a group is dispersed into a new part of the environment |
| Now suppose that we want to find the minimum of J(θ)where θ ÃâÃâ Rp (i.e. θ is a p-dimensional vector of real numbers), and we do not have measurements or an analytical description of the gradient ΔJ(θ). BFOA mimics the four principal mechanisms observed in a real bacterial system: chemotaxis, swarming, reproduction, and elimination-dispersal to solve this non-gradient optimization problem. A virtual bacterium is actually one trial solution (may be called a search-agent) that moves on the functional surface to locate the global optimum. Let us define a chemotactic step to be a tumble followed by a tumble or a tumble followed by a run. Let j be the index of the chemotactic step. Let k be the index of the reproduction step. Let l be the index of the elimination-dispersal event. Also let |
| p: Dimension of the search space, S: Total number of bacteria in the population, Nc : The number of chemotactic steps, Ns: The swimming length, Nre : The number of reproduction steps, Ned : The number of elimination-dispersal events, Ped : Elimination-dispersal probability, C (i): The size of the step taken in the random direction specified by the tumble. |
| Let P( j, k, l) {θi ( j, k, l) | i = 1,2,..., S} represent the position of each member in the population of the S bacteria at the j-th chemotactic step, k-th reproduction step, and l-th elimination-dispersal event. Here, let J (i, j, k, l) denote the cost at the location of the i-th bacterium θi ( j, k, l ) ÃâÃâ Rp (sometimes we drop the indices and refer to the i-th bacterium position as θi ). Note that we will interchangeably refer to J as being a “cost” (using terminology from optimization theory) and as being a nutrient surface (in reference to the biological connections). For actual bacterial populations, S can be very large (e.g., S =109), but p = 3. In our computer simulations, we will use much smaller population sizes and will keep the population size fixed. BFOA, however, allows p > 3 so that we can apply the method to higher dimensional optimization problems. Below we briefly describe the four prime steps in BFOA. |
| i) Chemotaxis ii) Swarming iii) Reproduction iv) Elimination and Dispersal |
| FLOW CHART: |
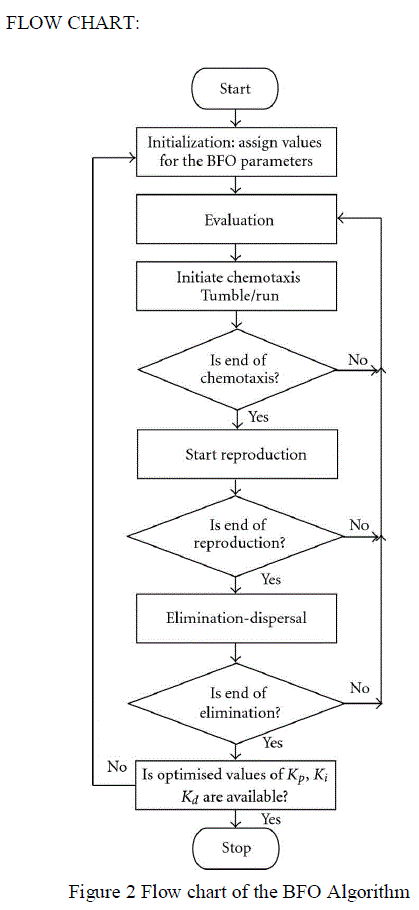 |
IV. EVALUATION AND COMPARISON |
| Waveforms with respect to the Kp, Ki values provided by BFOA |
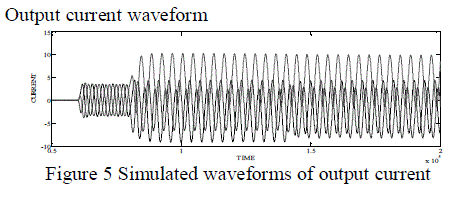
| waveforms, a normal signal waveform is obtained initially from 0.3 to 0.4 seconds. The Kp, Ki values obtained from BFO algorithm is applied at 0.4 seconds, which gives the improved output result. The voltage sag will be reduced at this point. The same technique is applied in all the following output waveforms that are obtained by the Kp, Ki values calculated by BFO algorithm. |
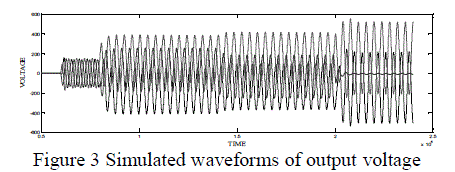 |
| Load voltage waveform |
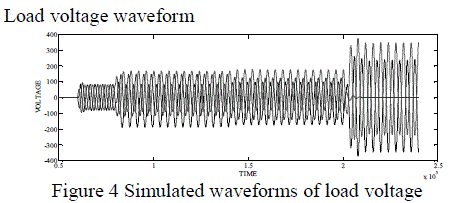 |
| Output current waveform |
 |
TOTAL HARMONIC DISTORTION (THD) RESULTS |
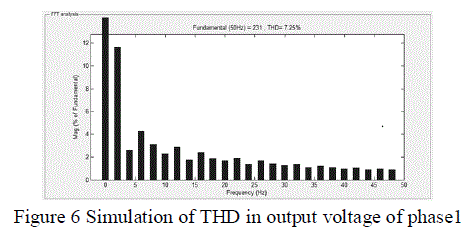
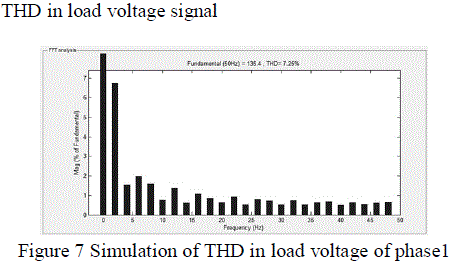
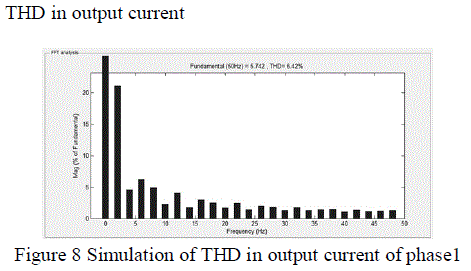
| The total harmonic distortion with respect to the Kp, Ki values that are calculated by Bacterial Foraging Optimization Algorithm are shown in the following figures. It can be observed by injecting those values into the PI controller. It gives different values at different phases. The harmonics obtained in output voltage, load voltage and the output current at different phases are shown. |
| THD of Kp, Ki values using BFOA THD in output voltage |
 |
 |
 |
V. CONCLUSION |
| In wind energy conversion system the DFIG is used. Wind energy conversion techniques using doubly fed induction generator for power quality improvement topology for optimal performance and reliability of the system. Variable speed wind generators are frequently used and are more attractive than fixed-speed systems because of their efficient energy production, improved power quality and dynamic performance during grid faults. Recently, the most of the wind energy conversion systems are equipped with a variable speed DFIG. It has both stator and rotor which will be used in high power applications. The Bacterial Foraging Optimization (BFO) algorithm is used in this paper to obtain the actual proportional and integral constants. The Kp and Ki values obtained from the BFO algorithm is applied in the PI controller. By using these values the power quality can be improved. The total harmonic distortion can be reduced. |
References |
|