ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Mahalakshmi.G1, Bhavani.M2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The rising demand for electric power, inadequate power generation and scarcity of transmission facilities forces the power system to be operated under stressed conditions. At heavily loaded conditions the power system must be provided with sufficient reactive power reserves in order to avoid voltage instability. Minimizing real power loss in transmission lines and the voltage deviation at the load buses in a power system is also essential. So optimization of reactive power plays a vital role in maintaining voltage stability and reducing real power losses of the power systems. In deregulated electricity market, reactive power provision needs to be made by Independent System Operator (ISO) in order to meet contracted transaction in a secure manner. So optimization of reactive power becomes essential in a deregulated power system environment because ISO chooses the optimum bidders based on real power cost characteristics and the reliability of power being delivered. In this paper reactive power flow problem is solved and Particle Swarm Optimization (PSO) technique is used for optimizing the values of generator voltage,transformer taps and switchable VAR sources. MATLAB is used for performing optimal power flow and formulating the algorithm for optimization of reactive power flow using PSO. IEEE-30 bus system has been used to evaluate the effectiveness of proposed system.
Keywords |
| Reactive power management, Restructured power system |
INTRODUCTION |
| Main objective of a power system is to meet the connected load to the maximum extent with the available generation in a secure, economic and reliable manner. The load consists of both active and reactive components. The transmission of power over AC circuits involvesreactive components. The generation of power too contains the reactive participation. Hence it is important and vital to monitor and controlreactive power resources and reactive power consuming elements to maintain proper voltages in the grid within safe and secure limits. Reactive power management thus forms the prime concern of power systems.The majority of the reactive power management objectives were to provide the least cost and less real power loss. Variants of this objective include the cost of real power losses, cost of VAR installation, voltage stability index and voltage deviation. However, the goal of RPM is to provide the system with efficient VAR compensation to enable the system to be operated under a balanced condition between security and economic concerns.Conventional power flow algorithms that were used in earlier days do not automatically minimize anyobjective functions such as fuel cost or real power transmission losses. They only obtain a single feasible solution. All the conventional methods have disadvantages such as time consumption, slow convergence, less accuracy, etc., and so the researchers moved towards intelligent techniques like Genetic Algorithm (GA), Simulated Annealing(SA), Tabu Search (TS), Particle Swarm Optimization (PSO), etc., In [1] optimal reactive power flow problem is analyzed using Back Propagation Neural Network in MATLAB. Results of this multi objective problem show that this method can be used for large power systems. Wei Yan [3] used a hybrid method based on GA and Interior Point Method (IPM). Ying Li [4] introduced a novel method in which Message Passing Interface based parallel computation and PSO algorithm were combined to form the Parallel Particle Swarm Optimization method for solving the Dynamic Optimal Reactive Power Dispatch problem. Optimization process is implemented on a multi-processor supercomputer to reduce the computational time drastically.Differential Evolution algorithm is used in [5] whereresults illustrate that in some cases even with reduction of losses, the impact on the stability is negative. |
| A PSO based optimal reactive power flow management with the incorporation of TCSC is proposed in [7]. PSO is used to determine the best location for TCSC with a level of compensation being considered as it sometimes leads to worst solution. In [8], [9] Modified Immune PSO and Gravitational Search Algorithm are usedrespectively for solving the reactive power flow problem and results are compared with the performance of GA, BOX algorithm, DE and classical PSO. LashkarAra [11] implemented Mixed Integer Non Linear Programming which is solved using ε-constraint method. General algebraic modeling system GAMS is used to solve the optimal model and MATLAB is used to feed parameters to the GAMS routineMandal 12] used a combination of Teaching Learning Based Optimization and Quasi Opposition Based Optimization which is known as QOTLBO both single and multi-objective functions are solved using IEEE 30 and IEEE 118 bus systems. Badar in [13] had optimized reactive power flow using dynamic PSO where active power loss is reduced by 20% and voltage profile is also improved. The optimization techniques like GA, EA, PSO, Big Bang – Big Crunch (BB-BC) algorithm and EP are used for reactive power optimization problem in [3], [14], [15], [17] and the comparative results are shown. Though the existing methods show better results there are some drawbacks such as slowconvergence, worst solution, and violation of limits. To overcome these drawbacks the proposed method of this paper used dynamic PSO and Bacterial Foraging Algorithm which results in attainment of good result along with fast convergence rate. |
II.REACTIVEPOWER MANAGEMENT |
| Reactive power management is one of the important tasks in the operation and control of the power system. Reactive power control problem can be formulated as a non-linear constrained optimization problem. Minimization of real power loss is the main objective of this reactive power optimization problem. However minimization of voltage deviation, real power cost and shunt reactor installation cost is also added to the objective function. The optimization part is solved by the PSO algorithm. The purpose of reactive power dispatch is mainly to minimize the real power transmission loss of the system and to improve the voltage profile while satisfying the unit and system constraints.The objective of this paper is to minimize the real power cost, real power loss, and reactive power source installation cost and voltage deviation of the IEEE 30 bus test system. |
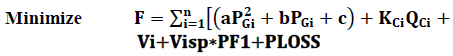 |
| (W2.h1e)r e PGi : Real power generated at bus i, QCi : Shunt power source at bus i, Vi : Voltage magnitude of bus i, Vi, sp : Desired voltage at bus i, PLOSS : System loss, a,b,c : Cost coefficients, PF1,PF2: Price penalty factor, |
| In vertically integrated power systems reactive power facilities are operated under monopoly by the ISO to meet technical requirements such as improving voltage profile, reducing losses of transmission lines, etc., and so there is no clear competition for providing reactive power as ancillary services.In normal operation state, the reactive power balance must be kept in such a way that the voltages are within acceptable limits. |
| The inequality between reactive power generation and consumption does not exist and the reactive power generated and consumed is always equal. Therefore, an improper reactive power generation and consumption level in the system will result in inappropriate voltage profile. |
| Unlike the active power ancillary services (frequency control reserves), the reactive power cannot be transmitted efficiently through long distances because it leads to additional active and reactive power losses. The reason is that the large reactive impedance of the high voltage transmission system causes reactive power loss. So the reactive power generation and consumption have to be as close as possible to each other to avoid excessive reactive power transmission.Inderegulated power systems there is more space for a utility to act as an ancillary service provider unlike the vertically integrated power systems. So if a utility chooses to provide ancillary service then it has the responsibility to manage the reactive power flow effectively. As reliability, cheap tariff and uninterrupted power supply are the major motives of deregulated power system, optimization of reactive power flow is an important task to be done in order to satisfy the needs of customers and be profitable to the utilities also. |
III.POWER FLOW EQUATIONS |
| Equality Constraints, |
| Real power constraint |
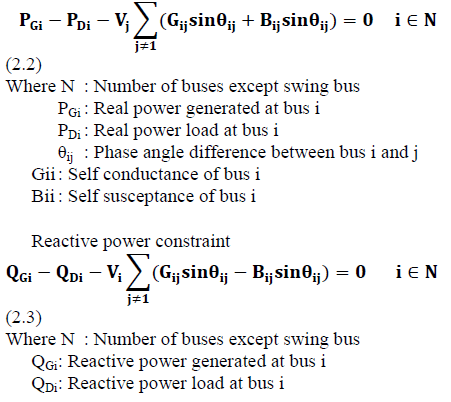 |
| Inequality Constraints, |
 |
IV.PARTICLE SWARM OPTIMIZATION |
| Particle Swarm Optimization is one of the AI techniques, inspired by the social foraging behavior of some animals such as flocking behavior of birds and the schooling behavior of fish. Particles in the swarm fly through a space of solutions. Particles follow the fittest member of the swarm and generally biasing their movement toward historically good areas of the provided space. To have all the particles being located in the optimal position in a multi-dimensional hyper-volume is the goal of this optimization technique. This is achieved by initiallyassigning random positions to all the particles in the provided space and small initial random velocities. On executing the algorithm the position of each particle is advanced based on its velocity, the best known global position in the problem space and the best known individual position of a particle. The objective function is evaluated after each position update. In this paper PSO had been used to optimize the values of control variables (generator voltage, transformer tap position and shunt reactor rating) and these are defined as the particles of PSO.Each particle tries to modify its position using the following information: |
| ïÃâ÷ Current positions, ïÃâ÷ Current velocities, ïÃâ÷ Distance between the current position and pbest, ïÃâ÷ Distance between the current position and gbest.Minimum and maximum values for control and state variables are set and random particles are generated. The counter is initialized to 1 and it is incremented each iteration. Power flow constraints are verified. OPF is executed for each and every particle using Interior Point Algorithm in MATPOWER4.1. This gives the values of active power loss, voltage deviation, real power cost and VAR installation cost which will be added to get the value of objective function or the fitness value for each particle. The individual best is updated for better fitness value of a particle. After updating all individual best, the global best is also updated. Based on the values of individual best, global best and random velocities, each particle is assigned a new position. On the end of iterations the results are displayed.The movement of the particle is governed by updating its velocity and position attributes. The velocity of particle is updated as, |
 |
 |
 |
VI.RESULTS |
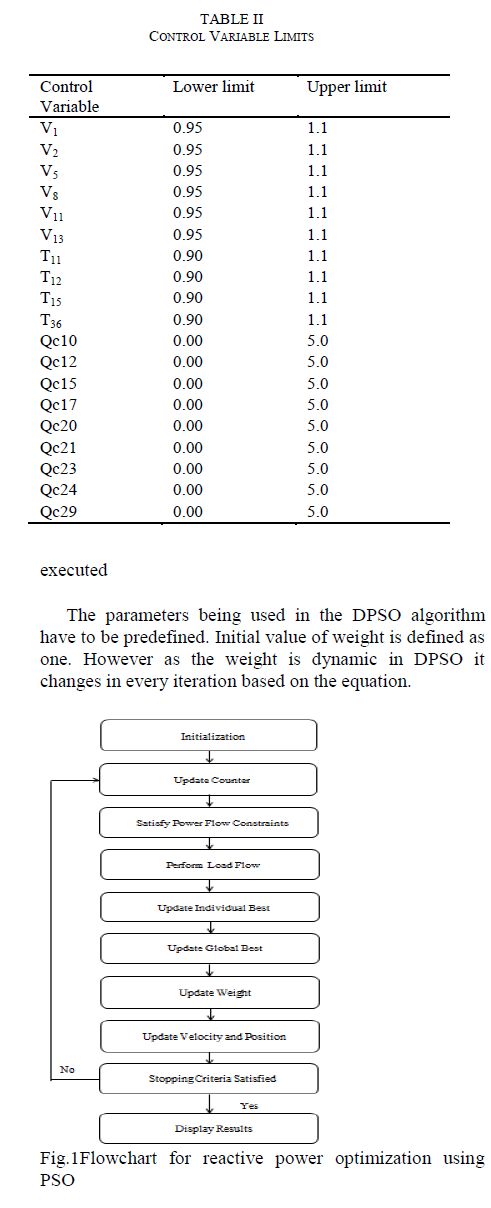
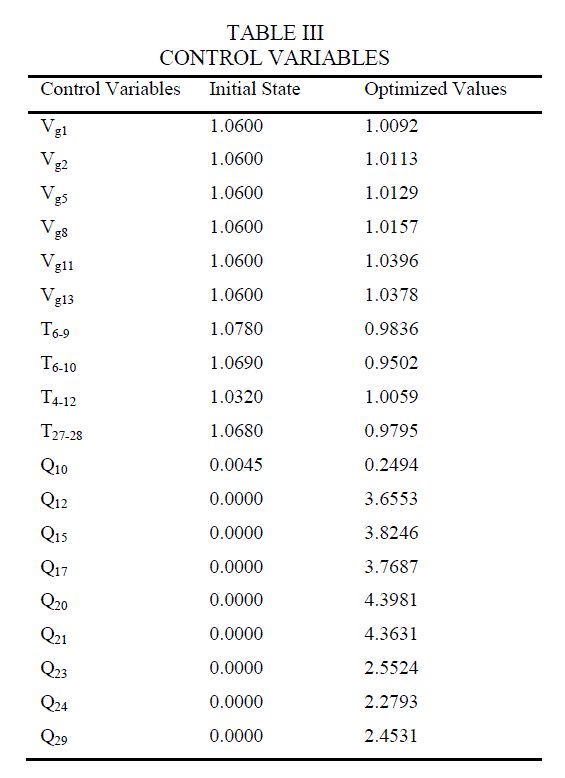
| Effectiveness of the proposed method has been tested using the standard IEEE 30 bus test system. Implementation of this method is done using MATLAB 2012 and MATPOWER 4.1 programs for performing optimal power flow. Line data and bus data are taken from [9] to perform optimal power flow. The limit of control variables is shown in Table II. Table III shows the values of the control variables generator bus voltage, transformer tap ratio and shunt reactor capacity at initial state and after optimization. From Table III it is clear that the optimized values of all the control variables reside within their corresponding limits. It has been observed that better results are obtained on setting these optimized values of control variables. The value of objective function is reduced on using these particular values. As well as real power loss, voltage deviation and real power cost are also reduced individually. |
 |
 |
 |
 |
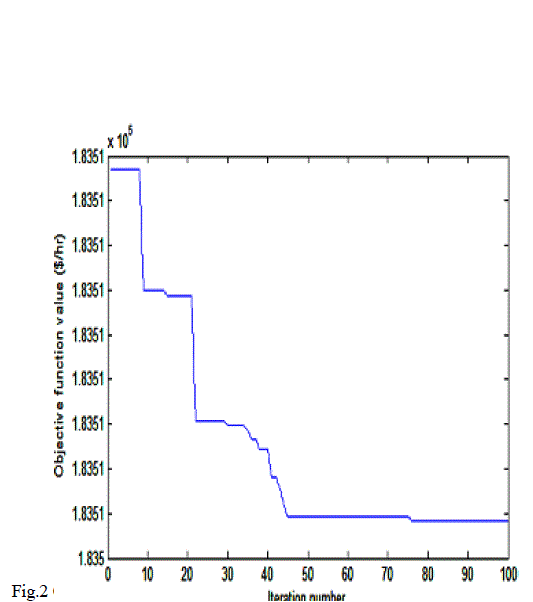
| Fig.2 shows the characteristics of objective function for the settings of optimized values of control variables. The value of objective function is reduced from 19504$/hr(base case) to183505$/hr(Dynamic PSO). |
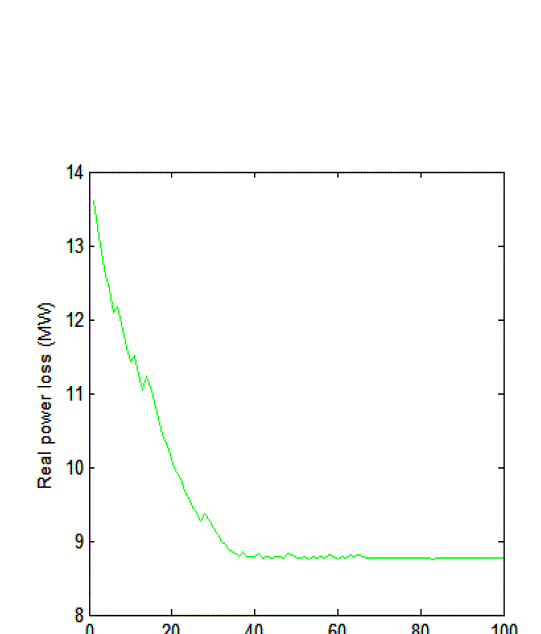
| Fig.3 shows the characteristics of real power loss which is reduced from 9.507MW to 8.7623MW after using the optimized values of control variables. |
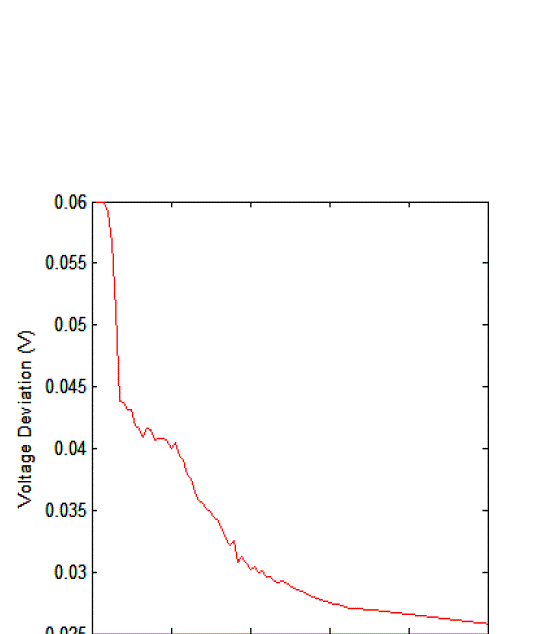
| The above graph plotted for iterations and voltage deviation shows that there is a reduction in voltage deviation is reduced to 0.03V.Though the reactive power control and voltage control are difficult to perform simultaneously in this paper both the power loss and voltage deviation are reduced concurrently. |
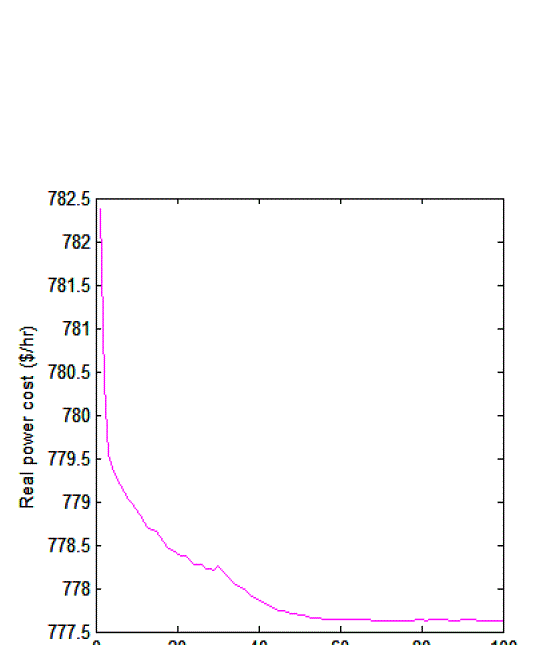
| In Fig.5 the variation of real power cost in each iteration has been plotted which indicates that the cost is reduced to a considerable value for the optimized values of control variables. |
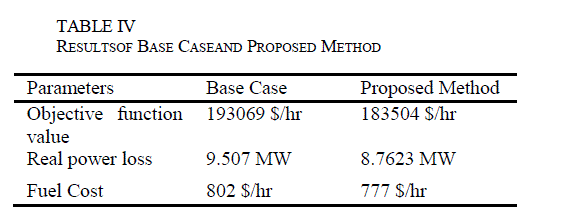 |
| Results obtained before and after optimization are shown in TABLE IV. Results of base case power flow are taken into account to evaluate the effectiveness of the proposed method. The convergence graphs Fig.2, Fig3, Fig.4, Fig.5 and TABLE IV clearly indicate that the objective of this paper is achieved. |
CONCLUSION |
| The proposed method has been implemented using IEEE 30 bus system to evaluate the performance of it. From the results it is seen that the objective function value, real power loss and real power cost have been reduced by 4.9%, 8.4% and 3.1% respectively on comparing with the base case results. Voltage deviation is also reduced to an acceptable value. It is clear that as the real power loss is reduced and voltage deviation is controlled, usage of reactive power is optimized using Dynamic PSO. |
References |
|