ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
K.Thulasi1, S.Sowmiyaa2, P.Prema3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
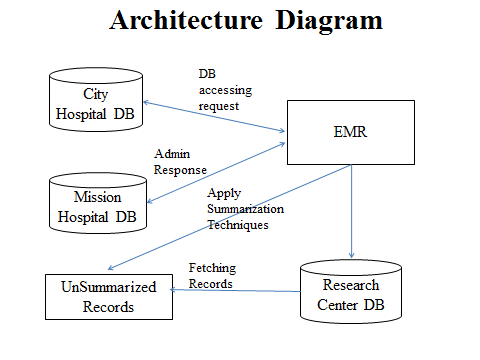
Early detection of patients with elevated risk of developing diabetes mellitus is critical to the improved prevention and overall clinical management of these patients. We aim to apply association rule mining to electronic medical records (EMR) to discover sets of risk factors and their corresponding subpopulations that represent patients at particularly high risk of developing diabetes.Given the high dimensionality of EMRs, association rule mining generates a very large set of rules which we need to summarize for easy clinical use. We reviewed four association rule set summarization techniques and conducted a comparative evaluation to provide guidance regarding their applicability, strengths and weaknesses. We proposed extensions to incorporate risk of diabetes into the process of finding an optimal summary. We evaluated these modified techniques on a real-world prediabetic patient cohort. We found that all four methods produced summaries that described subpopulations at high risk of diabetes with each method having its clear strength. For our purpose, our extension to the Buttom-Up Summarization (BUS) algorithm produced the most suitable summary. The subpopulations identified by this summary covered most high-risk patients, had low overlap and were at very high risk of diabetes.
Keywords |
| DataMining, Association Rules, Association Rule Summarization |
INTRODUCTION |
| Diabetes mellitus may be a growing epidemic that affects 25.8 million individuals within the U.S. (8% of the population), and just about seven million of them don't grasp they have the sickness polygenic disease results in vital medical complications as well as anaemia {heart disease|heart condition |cardiopathy |cardiovascular sickness}, stroke, renal disorder, retinopathy, pathology and peripheral vascular disease. Early identification of patients at risk of developing polygenic disease may be a major health care want. Appropriate management of patients in danger with manner changes and or medications will decrease the chance of developing diabetes by half-hour to hour. Multiple risk factors have been known touching an outsized proportion of thepopulation. as an example, pre diabetes (blood sugar levels above traditional vary however below the extent of criteria for diabetes) is gift in just about thirty fifth of the adult population and will increase absolutely the risk of polygenic disease three to ten fold counting on the presence of further associated risk factors, like avoirdupois, idiopathic, hyperlipemia ,etc. Association rules area unit implications that associate a group of potentially interacting conditions (e.g. high BMI and therefore the presence of cardiovascular disease diagnosis) with elevated risk. The use of association rules is predominantly worthwhile, because in addition to quantifying the polygenic disorder risk, they conjointly promptly provide the MD with a rationale, namely the associated set of conditions. This set of conditions is used to guide treatment towards a additional customized and targeted preventive care or polygenic disorder management. A number of winning association rule set report techniques are planned however no clear steering exists concerning the concernment, strengths and weaknesses of those techniques. the main target of this palimpsest is to review and characterize four existing association rule report techniques and supply steering to practitioners in selecting the foremost appropriate one. A common defect of those techniques is their inability to take polygenic disorder risk–a continuous outcome–into account. In order to form these techniques a lot of applicable, we had to minimally modify them: we tend to extend them to include information regarding continuous outcome variables. Specifically , our key contributions area unit as follows. 1. we tend to gift a clinical application of association rule mining to spot sets of co-morbid conditions (and the patient subpopulations who are suffering from these conditions) that imply considerably inflated risk of diabetes. 2. Association rule mining on this in depth set of variables resulted in AN exponentially massive set of association rules. we tend to extended four standard association rule set report techniques (mainly from the review ) by incorporating the chance of polygenic disorder into the method of finding AN best outline. 3. Our main contribution could be a comparative analysis of these extended report techniques that provides steering to practitioners in choosing an appropriate rule for an analogous downside. |
II. RELATED WORK |
| A polygenic disease index is in essence a prophetic model that assigns a score to a patient supported his calculable risk of polygenic disease. Collins conducted an intensive survey of polygenic disease indices describing the danger factors and also the modeling technique that these evidence used. They found that most indices were additive in nature and none of the surveyed indices have taken interactions among the danger factors into consideration. While we have a tendency to don't seem to be awake to any new polygenic disease index revealed after the survey, a recent study specializing in the metabolic syndrome (of that polygenic disease may be a component) represents a big development. Kim et al. Used association rule mining to consistently explore co occurrances of identification codes. The ensuing association rules don\'t constitute a polygenic disease index as a result of the study doesn't designate a particular outcome of interest and that they don't assess or predict the danger of polygenic disease in patients, but they discovered some vital associations between identification codes. We have recently undertaken a polygenic disease study wherever we aimed to get the relationships among diseases in the metabolic syndrome. We have a tendency to used identical cohort as this current study, however, we have a tendency to enclosed solely eight identification codes and age as predictors. We discovered association rules involving a number of these eight identification codes, assessed the risk of polygenic disease that these rules confer on patients and presented the principles as a progression graph portraying however patients progress from a healthy state towards polygenic disease. We incontestable that the approach found clinically meaningful association rules that square measure in step with our medical expectation. With solely eight predictor variables, the dimensions of the discovered rule set was modest–13 vital rules– and consequently, interpretation was simple. Naturally, no rule-set account was necessary. |
III. ASSOCIATION RULE MINING |
| Let associate degree item be a binary indicator signifying whether or not a patient possesses the corresponding risk issue. E.g. the item htn indicates whether or not the patient has been diagnosed with hypertension. Let X denote the artifact matrix, which is a binary covariate matrix with rows representing patients and the columns representing things. Associate degree itemset may be a set of items: it indicates whether or not the corresponding risk factors are all present within the patient. If they're, the patient is claimed to be covered by the itemset (or the itemset applies to a patient). An association rule is of kind I → J, wherever I and J are both itemsets. The rule represents associate degree implication that J is likely to use to a patient only if I applies. The itemset I is that the antecedent and J is that the resulting of the rule. The strength and “significance” of the association is traditionally quantified through the support and confidence measures. The support of associate degree itemset is that the variety of patients lined by that itemset and therefore the confidence of a rule R:I → J, is that the fraction of patients lined by J among those who are lined by I. In association rule mining, things don't play specific roles: there aren't any selected predictor variables or outcome variables. In alternative words, any item will seem within the antecedent of 1 rule and within the resulting of another. Predictive association rule mining , diagrammatical the first departure from this paradigm by designating a specific item as AN outcome. the ensuing of the prophetical association rules is often the selected outcome item. Regressive association rules and quantitative association rules more swollen this paradigm permitting a continuous outcome variable y to function the “consequent” of a rule. Let y(I) denote the end result within the subpopulation of patients that's lined by I; there's one y(I) worth for each patient. Further, let Ãâ¹Ãâ°y(I) denote the subpopulation mean outcome, the mean of y(I) values across patients to whom I applies. Analogously to the first association rule formulation, regressive association rules also are implications: they state that patients World Health Organization gift condition(s) I (antecedent) have outcome ¯y(I) on the average. |
| Suppose that y denotes never-ending variable that quantifies the chance of polygenic disease. By examination the population mean outcome ¯y(I) for the affected population (patients who gift the antecedent I) to the mean outcome ¯y(¬I) of the unaffected population (patients missing a minimum of one condition from I), we will assess the importance of I as a risk issue. as an example, if y denotes the quantity of diabetes events then the metric RR = ¯y(I)/¯y(¬I) is named the relative risk and it signifies that patients with condition(s) I are RR times additional probably to get to polygenic disease than patients missing a minimum of one condition from I. Unfortunately, in some cases, the distinction within the outcome between these two subpopulations can't be sufficiently captured victimisation the mean outcome, sometimes the spatial arrangement kind of the result conjointly plays a task. Distributional association rule will capture such variations. |
IV. METHODS |
| Applying our methodology of mixing spacing association rule mining with survival analysis made a combinationally sizable amount of (statistically significant) rules. Many of those rules square measure slight variants of every alternative leading to the obfuscation of the clinical patterns underlying the ruleset. One remedy to the current downside, that constitutes the main focus of this work, is to summarize the ruleset into a smaller set that's easier to summary. |
| We first review the present rule set and info summarization ways, then propose a generic framework that these ways fit into and finally, we tend to extend these methods in order that they'll take endless outcome variable (the martingale residual in our case) under consideration. |
Summarization Based on Greedy Set Coverage |
| Summarization ways supported greedy set coverage share a typical downside formulation as follows: given a loss criterion L, construct a group A consisting of k itemsets all drawn from I or a superset of I specified A minimizes L. The problem is NP-hard Associate in Nursingd an approximate answer is obtained victimization some variant of sequential coverage. |
Algorithm 1 Sequential coverage |
| Input: Set I of itemsets, number k of summary rules Output: Set A of itemsets, s.t. A minimizes the criterion L Generate an extended set E of itemsets based on I A = _ while |A| < k do A = arg min E∈E L(E) Add A to A Remove the effect of A end while |
| Algorithm one describes the define of the sequential coverage algorithmic rule. 1st a group E of itemsets is spawn, which forms the gathering of itemsets from that the outline rules A square measure hand-picked. usually E is that the similar as I, but some algorithms add further itemsets, creating it a superset of I. ab initio A is empty and it's made iteratively. In every iteration, the rule E in E that minimizes L is chosen and additional to A. To avoid choosing constant rule repeatedly, its impact is removed: either the rule itself is discarded from E or the patients coated by the rule square measure far away from the data set (so that the criterion isn't evaluated over these patients). |
| The key someone among the algorithms is that the definition of the loss criterion. The loss criterion is developed such that it incorporates info regarding the expression of the rule further because the patient coverage of the rule. Unfortunately, with the doable exception of TopK , none of the strategies incorporate associate outcome live like the risk of polygenic disorder. |
 |
V. TECHNIQUES |
| APRX - COLLECTION. This algorithm summarizes itemsets in I solely based on the expression (items) of the itemset [1]. To illustrate the key idea behind APRX-COLLECTION, consider a set I of itemsets, I ={abc, abd, bcd, ab, ac, ad, bc, cd, a, b, c, d}. This set of itemsets can be covered with a single itemsetabcd, which introduces only one sub itemset not present in the set (false positive): acd. Note that abcd is not in I. Therefore, first, APRX-COLLECTION creates an extended set E of itemsets through extending the itemsets in I by one or two items. Then, it selects the rule E from E that covers the most rules in I provided that E has a false positive rate less than α,which is a user-defined parameter. Formally, a false positive occurs when a subset E’ of E is not present in I. The false positive rate is the number of false positives over the total number of rules covered. The loss criterion for a rule E in E is then defined as Laprxc (E) ={−|S E |, if false positive rate < α 0, otherwise, where SE denotes the set of rules in I (!) covered by E. Once a rule E is selected, it is added to A. E itself and all rules covered by E are removed from E. |
| RPGlobal.RPGlobal constructs A from I without extending the set of rules: that is, E = I . It still chiefly operates on the expression of the rule, but it takes patient coverage into account through the RPC. The selection criterion is that each itemset E in A covers a maximal number of itemsets in I and those itemsets differ from E in patient coverage by no more than 1−δ, where δ is a user-defined parameter. The loss criterion then can be formulate Lrpglobal (E) ={−|S E |, if ∀I ∈ S E , RPC(E, I) > 1 − δ 0, otherwise. Once a rule E has been selected, E and all rules covered by E (S A) are removed from E. |
| TopK.Unlike the previous algorithms, TopK primarily operates on the patients as opposed to the rules. In addition, it introduces the concepts of significance and redundancy. In our context significance corresponds to y, the risk of diabetes. When multiple rules cover the same patient, redundancy arises. Let us assume that rule A has already been selected and we are considering rule E for inclusion into A. Further assume that a patient exists who is covered by both A and E. In that case, some of the risk this patient is exposed to has already been accounted for by A. In this spirit, the algorithm aims to construct A from I (without extending it; E = I) such that the significance of A is maximized while the redundancy of A is minimized. Formally, the redundancy of an itemset A with respect to another itemset I is redundancy(A, I) = RPC(A, I) min(y(A), y(I)). |
| RPC(A, I) is the similarity in patient coverage, the fraction of patients that are doubly covered, and min(y(A), y(I)) can be thought of as the part of the risk already accounted for by the rule already selected. When no patient is covered by both A and I, redundancy is 0; when A and I are identical, redundancy is y(A) (y(A) = y(I)). The redundancy of an itemset I with respect to a set A of itemsets is Redundancy (A,I) = max redundancy(A, I) |
| A∈A =max RPC(A,I) min(y(A), y(I)). A∈A The selection criterion of the algorithm is Ltopk (E) = redundancy(A, E). Since redundancy(A, E) is maximal for an E already in A, there is no need to remove E or the patients covered by E. |
| BUS. BUS represents the far end of the spectrum in terms of assigning importance to the expression of the rule versus the patient coverage information [6]. The objective of BUS is to construct a good summary of the data set (as opposed to constructing a good summary of the rule set).To this end, BUS utilizes an extended set E, which is the union of the itemsets in I and the individual transactions themselves D. Such an extended set is beneficial for example when outliers are present: if no itemset in I describes a transaction adequately, the transaction itself can be added to the summary. BUS incrementally selects itemsets E from E such that E maximizes the support and the data coverage. Formally, the selection criterion is Lbus (E) = −|DE | − DC(E). Once a rule E has been selected and added to A, all patients covered by E are removed from the data set. |
VI. CONCLUSION |
| The electronic information generated by the utilization of EMRs in routine clinical follow has the potential to facilitate the invention of new information. Association rule mining coupled to a summarization technique provides a important tool for clinical analysis. It will uncover hidden clinical relationships and can propose new patterns of conditions to send determent, management, and treatment approaches. |
| While all four strategies created cheap summaries, each methodology had its clear pith. However, not all of these strengths ar essentially beneficial to our application. We found that the foremost necessary mortal between the algorithms is whether or not they use a range criterion to include a rule out the outline supported the expression of the rule or supported the patient population that the rule covers. |
| APRX-COLLECTION and RPGlobal on the whole operate on the expression of the principles with a primary objective of maximizing compression. They use emblematic rules, each of that represents variety of original rules. Such representative rules win terribly high squeezing, but dilute the risk of polygenic disease over the generally massive population they cover. |
| TopK and BUS operate totally on the patients and their objective–especially just in case of TopK–can be thought of as minimizing redundancy. They created smart summaries as a result of a beneficial facet result of reducing redundancy is to realize smart compression. The converse is not true: high compression rate doesn't lead to low redundancy. |
| Between TopK and BUS, we tend to found that BUS maintained slightly additional redundancy than TopK, that allowed it to own higher patient coverage and higher ability to reconstruct the initial information base. This advantage created BUS the best suited rule for our purpose. |
References |
|