ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
P.Nithya1 and M.Lakshmi prabha2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Preserve privacy data using sTile methods addresses the challenge of executing computations on untrusted machines in a trustworthy manner. Its focus is on preserving data privacy while solving computationally intensive problems on untrusted machines. Existing work presented sTile technique for building software systems that distribute large computations onto the cloud while providing guarantees that the cloud nodes cannot learn the computation’s private data. sTile is based on a nature-inspired, theoretical model of self-assembly. In this paper, we present a prototype implementation that solves NP-complete problems. sTile explores the fundamental cost of privacy through data distribution. Tile assemblies are Turning universal, so future extensions of sTile can be made to perform arbitrary computations and to automatically compile programs into tile assemblies.
Keywords |
| Self-assembly, Adder,Multiplier; sTile,Tile assembly model |
INTRODUCTION |
| The emergence of cloud computing is evolving the nature of computation. Instead of using private machines, users allow the cloud to maintain, manipulate, and safeguard their data. This evolution has allowed ubiquitous access to computation and data with higher availability and reliability than possible with personal machines and local servers. This paper addresses the challenge of executing computationson untrusted machines in a trustworthy manner. Its focusis on preserving data privacy while solving computationallyintensive problems on untrusted machines.We present sTile, a technique for building softwaresystems that distribute large computations onto the cloudwhile providing guarantees that the cloud nodes cannotlearn the computation’s private data. sTile is based on anature-inspired, theoretical model of self-assembly. WhilesTile’s computational model is Turing universal, in thispaper, we present a prototype implementation that solvesNP-complete problems.sTile explores the fundamental cost of privacy throughdata distribution. |
| Self-assembly, the process by which objects autonomouslycome together to form complex structures,is omnipresent in the physical world. A systematic study ofself-assembly as a mathematical process has been initiated.The individual components are modelled as square tileson the infinite two-dimensional plane. Each side of a tileis covered by a specific “glue”, and two adjacent tileswill stick iff they have matching glues on their abuttingedges. |
| sTile computes while preserving privacy by breaking a computationinto small pieces and distributing those pieces onto alarge network. Each piece is so small that it is prohibitivelydifficult for an adversary to collect enough pieces to reconstructthe confidential data. |
| Existing approaches to using the Internet’s computational resources either assume reliable and trustworthy underlying machines only store data privately and rely on trusted entities to compute or are theoretical constructs (e.g., quantum computing and homomorphic encryption ) that, to date, have not produced implementations efficient enough for practical use. We evaluate sTile in three ways: 1.First, we formally prove that sTile systems preserve data privacy as long as no adversary controls more than one-half of the cloud. 2.Second, we empirically demonstrate sTile’s feasibility by deploying an open-source, publicly available prototype implementation on three distinct networks, including the globally distributed PlanetLabtestbed . |
| Department of CIVIL, CSE, ECE, EEE, MECHNICAL Engg. and S&H of Muthayammal College of Engineering, Rasipuram, Tamilnadu, India Copyright to IJIRSET www.ijirset.com 228 3.Third, we formally analyze the communication and computation costs induced by sTile, bound them, and empirically verify those bounds. sTile significantly outperforms existing cryptography-based privacy techniques, such as homomorphic encryption |
2.CONCEPTS |
2.1 Addition |
| sTile preserves privacy by breaking a computation into small pieces and distributing those pieces onto a large network. Each piece is so small that it is prohibitively difficult for an adversary to collect enough pieces to reconstruct the confidential data. In this section, we describe sTile with an example of distributing an addition computation.To describe adding using sTile, we explain three separate elements of our solution: i) The addition tile assembly, ii) The distribution process iii) The source of privacy. |
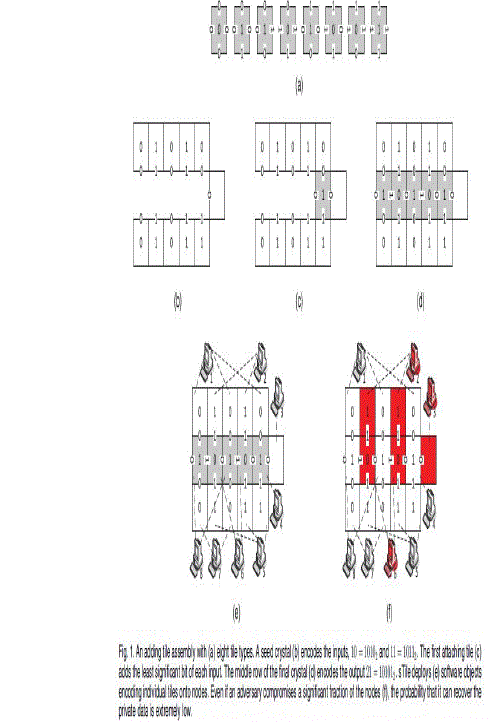
| i)The Addition Tile Assembly A tile assembly is a theoretical construct, similar to cellular automata. It consists of square tiles with static labels on their four sides. Tiles can attach to one another or to a growing crystal of other tiles when sufficiently many of their sides match. Fig. 1a shows eight different types of tiles used for addition. These tile types are the program—the tile assembly encoding of the algorithm for adding two integers, in binary, one bit at a time. Fig. 1b shows a seedcrystal that encodes an input: 10 (1010 in binary) in the top row and 11 (1011 in binary) in the bottom row. When an instance of a tile from Fig. 1a matches the seed crystal onthree sides, that tile instance attaches to the crystal. Fig. 1cshows the seed with a single attached tile. Note that this tileadds the least significant bit of each input: 0 þ 1 ¼1,displayed in the center of the newly attached tile. The labelon the west side of the newly attached tile is the carry bit: 0.The tiles execute full adder logic to add the bits, one at atime, eventually producing the sum 21 ¼ 101012 in themiddle row of Fig. 1d. |
| ii)The Distribution Process sTile uses the theoretical tile assembly to decompose acomputation into small parts. Each small part represents atile. Fig. 1e shows how the 10 þ 11 execution might bedeployed on eight network nodes. Each node only deploystiles of a single type, designated by the client machines . The client sets up a seed on thenetwork by asking nodes that can deploy tiles ofappropriatetypes to deploy instances of thdeploying and maintains references to the geometrically adjacent tile instances on other nodes. Next, tiles with an empty adjacent location coordinate with their crystal neighbors to recruit matching tiles to attach. Once the execution finishes, the tiles in the middle row report the solution to the client, indicating the node IDs of their crystal neighbors, which the client uses to reconstruct the output. |
| iii)The Source of Privacy Each tile instance is aware of only a single bit of the input, output, or intracomputation data, and not of the bit’s global location. An adversary may attempt to reconstruct the confidential data from the nodes it controls. For example,Fig. 1f shows an adversary that has compromised threenodes (2, 3, and 6), and now has access to the data infive tiles. However, this adversary can only tell that thereare some 0 and 1 bits scattered throughout the input, thecomputation, and the output, but not how many and nottheir relative positions. In fact, in this example, no threenodes contain the entire input (nodes 1, 2, 5, and 7 deploythe input). |
2.2 sTILE |
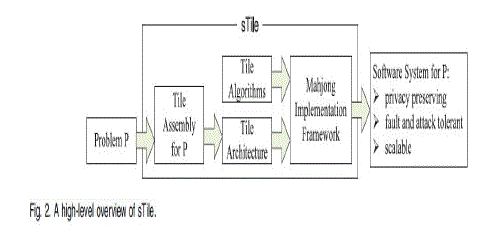
| sTile is a technique for designing, implementing, and deploying software systems that distribute computation onto large, insecure, public networks. sTile’s primary concern is to perform computation while preserving the privacy of the involved data.Figure 2shows a high-level overview of sTile |
 |
| sTile consists of four components: 1.Atileassembly 2.Thecorresponding tile architecture and the associated algorithms |
| sTile consists of four components: 1.Atileassembly 2.Thecorresponding tile architecture and the associated algorithms |
| 2.2.1 Computing with Tiles A key component of sTile is a tile assembly.Tile assemblies are theoretical objects that have no notionof privacy, although it is their basic structure that allowssTile to preserve privacy. sTile is a reification of a tileassembly as a distributed software system. |
 |
 |
| Figure 3 shows the 64 possible types of tiles of the 3-SATsolvingassembly. The tiles “communicate” via their sideinterfaces. Some interfaces contain a 0 or a 1, communicatinga single bit to their crystal neighbors. Other interfacesinclude special symbols such as v and :v indicating that avariable is being addressed, ? meaning that a comparisonshould take place, ? meaning the given tile attachesnondeterministically, and j and k indicating the correctnessof the computation up to this point. |
| 2.2.2 Tile Architecture and Algorithms AsTile-based system is a software system that uses a network of computers to solve a computational problem. Intuitively, the network simulates a tile assembly: Each computer pretends to be a tile or many tiles, and communicates with other computers to selfassemble a solution to a computational problem. Each computer deploys tile components, each representing a tile in a tile assembly, and facilitates the proper communication channels and algorithms to allow thetile component self-assembly. Thus, a tile architecture isbased on a tile assembly; the software system employing that architecture solves the particular computational problem that the tile assembly solves. |
| 2.2.3 Mahjong implementation framework. The final element of sTile is the Mahjong implementation framework which uses the tile architecture and algorithms to automatically compose a sTile-based software system on a network. The opensource Mahjong framework is realized as a Java-based middleware platform that faithfully implements the tile architecture and its algorithms. Mahjong’s implementation uses Prism-MW, amiddleware platform that provides explicit implementation- level constructs for declaring components, interfaces, interactions, network communication. |
3.COMPUTATIONAL FEASIBILITY |
| To demonstrate that sTile is a feasible solution for building software systems that distribute computationally intensive problems on very large networks, we must show that 1) such systems’ computational speed is proportional to the size of the underlying network, 2) such systems are robust to network delay, 3) real-world-sized problems can be solved on realworld- sized networks in reasonable time. |
| 3.1 sTile-Based Implementations Simjong is a Java-based discrete-event simulator with network-delay simulation capabilities. Simjong executes on a single machine and creates a userspecified number of virtual hardware Node components, each capable of deploying tiles. A central Clock component keeps track of virtual time and allows each Node to execute one instruction per clock cycle. While executing, Simjong keeps track of the number of completed seeds and reports its progress. Thus, it is possible to use Simjong to estimate the time required for a computation to complete after executing only a fraction of that computation. 3.2 Experimental Setup We use three distributed networks for our experimental evaluation: 1) a private heterogeneous cluster of 11 Pentium 41.5- GHz nodes with 512 MB of RAM, running Windows XP or 2000; |
| 2) a 186-node subset of USC’s Pentium 4 Xeon 3-GHz High Performance Computing and Communications cluster 3) a 100-node subset of PlanetLab, a globallydistributed network of machines of varying speeds and resources that were often heavily loaded by several experiments at a time. |
| The cross section of data we present in this paper usedfourrepresentative instances of NP-complete problems, towhich we will refer by their labels: A: 5-number 21-bit SubsetSum problem, . B: 20-variable 20-clause 3-SAT problem, C: 11-number 28-bit SubsetSum problem, |
| D: 33-variable 100-clause 3-SAT problem. Our experimental goals were to verify sTile’s scalabilitywith respect to network size and robustness to networkdelay. Our experiments had three independent variable: |
| 1. The number of nodes, 2. The network communication speed between nodes 3. The size of the NP-complete problem— and one dependent variable—the time the computation tookto complete. |
| First, to verify the correctness of sTile-based systems,we used Mahjong-based implementations to solve overone hundred of SubsetSum and 3-SAT problems, includingA, B, and C. As a rule of thumb, we chose the sizes ofproblem instances to each execute in under 4 hours on our186-node cluster. We verified that, on each of the abovethree networks, the implementations found the correctsolution to each instance, it sent no unexpected communication betweennetwork nodes and no node produced undesired connections between tile components. Further,we verified that, when provided inputs with a negativeanswer, the implementations continued to execute indefinitely,as expected . |
| 3.3 Scalability To verify that the speed of the computation is proportional to the number of nodes on the underlying network, for each of the three networks described above, we deployed Mahjong-based implementations on the entire network and on randomly selected halves of the network. We varied the size of the problem and measured the average time in which the implementations found the solution over 20 executions. We then also deployed Simjong on virtual networks of increasing size from 125,000 to 1,000,000 nodes. This allowed each Simjong execution to complete in about an hour of actual time, while executing a sufficiently large number of seeds. Our measurements have shown that, after the first few thousand seeds, our implementations make fairly constant progress through the seeds and that extrapolating from the 10_4 percent fraction is accurate. |
| 3.4 Robustness to Network Latency Intuitively, high-network latency should adversely affect the speed of sTile-based systems: If the tile attachments happen sequentially, the latency affects every attachment and greatly slows down the overall computation. However, in the case of NP-complete computations, this intuition is false. In such computations, many of the tile attachments happen independently,in parallel. Each node in our experiments deployed millionsof lightweight tiles, and whenever a sTile packet traveled between nodes, those nodes handled other tiles rather thanwaiting idly for the network communication to arrive. As aresult, the throughput of sTile-based systems is not affectedby the network latency. |
4.PRIVACYPRESERVATION |
| sTile’s privacy preservation comes from each tile being exposed only to a few intermediate bits of the computation and the tiles’ lack of awareness of their global position. To learn meaningful portions of the data, an adversary needs to control multiple, adjacent tiles. We call a distributed software system privacy preserving if, with high probability, a randomly chosen group of nodes smaller than half of the network cannot discover the entire input to the computational problem the system is solving. We argue that neither |
| i) a node deploying a single tile, nor ii) a node deploying multiple tiles can know virtually any information about the input; moreover, iii) controlling enough computers to learn the entire input is prohibitively hard on large networks. 1.Each tile type in an assembly encodes at most one bit of the input. A special tile encodes the solution, but has no knowledge of the input. A node that deploys a single tile is only able to learn information such as “there is at least one 0 bit in the input,” which is less than one bit of information. 2. Each node on the network may deploy several tiles. However, each tile is onlyaware of crystalneighboring tiles and not of itsglobal position. Thus, a node deploying severalnoncrystal-neighboring tiles cannot reconstruct anymore information than if it only deployed a singletile. The only way the node may gain moreinformation is if it deploys crystal-neighboring tiles. 3. Suppose an adversary controls a subset of thenetwork nodes and can see all the informationavailable to each of the tiles deployed on thosenodes. Then, the adversary can attempt toreconstructthe computation’s input from parts of thecrystal that consist of tiles deployed on the compromisednodes. |
5.RELATEDWORK |
| Distributing computation:The growth of the Internet has made it possible to use public computers to distribute computation to willing hosts. This notion focuses theunderpinning of computational grid . Among systemsthat concentrate on distributed computation are BOINCsystems (such as SETI@home andFolding@home ), MapReduce , and the organic grid . A uniqueapproach—FoldIt—uses the competitive human nature tosolve the protein-folding problem . These systems try tosolve exactly the highly parallelizable problems towardwhich our work is geared, but unlike sTile, they do notpreserve privacy. |
| Cloud privacy:Cloud computing has reemphasized theimportance of data privacy, causing the emergence ofnumerous approaches for keeping data private on the cloud. Most such approaches concentrate onprivate data storage and user-authorized data retrievalandrequire some trusted agents whereas our workconcentrates on preserving privacy during computationandrequires no trusted agents. |
| Privacy-preserving computation:In classical computing, it is not possible to get help from asingle entity in solving an NP-complete problem withoutdisclosing most of the information about the input and theproblem one is trying to solve [19]. Our approach avoidsthis shortcoming by distributing such a request over manymachines without disclosing the entire problem to anysmall-enough subset of them. |
6.CONTRIBUTIONS |
| sTile distributes computation onto large, insecure, public networks in a manner that ensures privacy preservation, fault and adversary tolerance, and scalability. We presented a rigorous theoretical analysis of sTile and formally proved that the resulting systems are efficient and scalable, and that they preserve privacy as long as no adversary controls half of the public network. We |
| We deployed two sTile implementations on several networks, including the globally distributed PlanetLab, to empirically verify 1.The correctness of sTile algorithms, 2.The speed of sTile computation is proportional to the number of nodes, 3.Network delay has a negligible effect on th speed of the computation, and 4.Mathematical analysis of the time needed to solve large problems on large networks is accurate. For networks larger than about 4,000 nodes, sTileoutperforms optimized solutions that assume privately owned, secure hardware. |
| sTile explores the fundamental cost of achieving privacythrough data distribution and bounds the extent to which aprivacy-preserving system is less efficient than a nonprivateone. While that cost is not trivial, we have demonstratedthat sTile-based systems execute orders of magnitude fasterthan homomorphic encryption systems, the alternativepromising approach to preserving privacy |
| In this paper we conclude that the proposed work demonstrated how sTile can solve 3-SAT (Satisfiability). sTile solves all NP-complete problems without designing new assemblies. NP-complete computation can be accelerated by developing faster algorithms for single machines and small clusters. Such work is complementary to ours since sTile is based on a Turing-universal computational model and can implement each of these advanced algorithms on large distributed networks. |
References |
|