Privacy Preserving Data Mining (PPDM) For
Horizontally Partitioned Data

Mohasin Tamboli; Jayapal PC Bhalerao M

Privacy Preserving Data Mining (PPDM) For Horizontally Partitioned Data

Mohasin Tamboli, Jayapal PC Bhalerao M.
Dept. of Information Technology, Vishwabharati Academy’s College of Engineering, Ahmednagar, Maharashtra, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Due to the increase in sharing sensitive data through networks among businesses, governments and other parties, privacy preserving has become an important issue in data mining and knowledge discovery. Privacy concerns may prevent the parties from directly sharing the data and some types of information about the data. This paper proposes a solution for privately computing data mining classification algorithm for horizontally partitioned data without disclosing any information about the sources or the data. The proposed method (PPDM) combines the advantages of RSA public key cryptosystem and homomorphic encryption scheme. Experimental results show that the PPDM method is robust in terms of privacy, accuracy, and efficiency. Data mining has been a popular research area for more than a decade due to its vast spectrum of applications. However, the popularity and wide availability of data mining tools also raised concerns about the privacy of individuals. The aim of privacy preserving data mining researchers is to develop data mining techniques that could be applied on databases without violating the privacy of individuals. Privacy preserving techniques for various data mining models have been proposed, initially for classification on centralized data then for association rules in distributed environments.

Keywords

Privacy, Data Mining, Distributed Clustering, Security, public key, RSA

INTRODUCTION

Data mining is an important tool to extract patterns or knowledge from data. Data mining technology can be used to mine frequent patterns, find associations, perform classification and prediction, etc. The data required for data mining process may be stored in a single database or in distributed resources. The classical approach for distributed resources is data warehouse. Fig. 1 shows a typical distributed data mining approach for building a data warehouse containing all the data. This requires the warehouse to be trusted and maintains the privacy of all parties. Since the warehouse knows the source of data, it learns site-specific information as well as global results. What if there is no such trusted authority? In a sense, this is a scaled-up version of the individual privacy problem; however it is an area where the Secure Multiparty Computation approach is more likely to be applicable. In this paper, RSA public key cryptosystem and homomorphic encryption are used to develop a reliable privacy-preserving data mining technique for horizontally partitioned data.Homomorphic encryption is a type of encryption method which lets specific kind of computations to be carried out on cipher text and get an encrypted result which decrypted matches the result of operations performed on the plaintext. For eg, one person can add two encrypted numbers and then another person can decrypt a result, without either of them can be to find the value of the individual numbers.

This is a desirable feature in modern communication system architectures. Homomorphic encryption will allow the chaining together of different services without exposing the data to each of those services, for eg a chain of different services from different companies could calculate the tax, the currency exchange rate, shipping, on a transaction without exposing the unencrypted data to each of those services. Homomorphic encryption schemes are flexible by design. The homomorphic property of all types of cryptosystems can be used to create secure voting systems, collision-resistant hash functions, and private information retrieval schemes and enable widespread use of cloud computing by ensuring the confidentiality of processed data. There are several efficient, partially and number of totally homomorphic, but less effective cryptosystems. Although a cryptosystem which is by accident homomorphic can be subject to attacks on this basis, if cured carefully homomorphism could also be used to perform computations securely.

II.BACKGROUND

This part is presents a brief view about the data mining algorithm used, the form of distributed data as well as the tools and techniques which are used for privacy – preserving during data mining process.

Data Mining Technique and Distributed data

A. The k-Nearest Neighbour Classifier: Standard data mining algorithm K-nearest neighbour classification is an instance based learning algorithm that has been shown to be very effective for a variety of problem areas. The aim of knearest neighbour classification is to discover k nearest neighbors for a given instance, then assign a class label to the given instance according to the majority class of the k nearest neighbours. The nearest neighbours of an Instance are defined in terms of a distance function such as: The standard Euclidean distance:

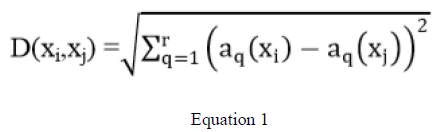Where r is the number of attributes in a record instance x ,ai(x) indicate the ith attribute value of record instance x, and D(xi, xj) is the distance between two instances xi, xj .

B.Vertically and Horizontally Data Partition

When the input to a function is distributed among different sources, the privacy of each data source comes into question. The way in which the data is distributed also plays an important role in defining the problem because data can be partitioned into many parts either vertically or horizontally .Then Vertical partitioning of data implies that different sites or organizations gather different information about the same set of entities or people, e.g hospitals and insurance companies collecting data about the set of people which can be jointly linked. So the data to be mined is the join of data at the sites. In horizontal partitioning, the organizations collect the same information about different entities or people. As an example supermarkets collecting transaction information of their clients. As a result, the data to be mined is the union of the data at the sites. In this report it is supposed that all organizations or departments that to be mined have the same information (homogenous) but different entities (records or tuples), so horizontal approach is conducted.

C. Privacy - Preserving Tools and Techniques

Secure Multi -Party Computation (SMC):SMC concept was introduced by Yao where he gave a solution to two millionaire’s problem. Each of the millionaires wants to know who is richer without disclosing individual property and wealth. This idea was further extended by Mr.Goldreich et al. to the multi party computation problem. The aim of a secure multiparty computation task is for the participating parties to securely compute some function of their distributed and private inputs. Each party learns nothing about other parties except its input and the final result of data mining algorithm. As an example considers the scenario where a number of distinct, yet connected, computing devices (or parties) wish to carry out a joint computation of some function. Let n parties with private inputs x1,…,xn wish to jointly compute a function f of their inputs. This joint computation should have the property that the parties learn the correct output y=f(x1,…,xn) and nothing else, and this should hold even if some of the parties maliciously attempt to obtain more information. The function f represents a data mining algorithm that is run on the union of all of the xi’s.

Digital Envelope: A digital envelope is a random number (or a set of random numbers) only known by the owner of private data used to hide the private data. A set of mathematical operations are conducted between a random number (or a set of random numbers) and the private data. The mathematical operations could be the addition, the subtraction, multiplication, etc. For example, assume the private data value is À. There is a random number R which is only known by the owner of À. The owner can hide À by adding this random number, e.g., À + R.

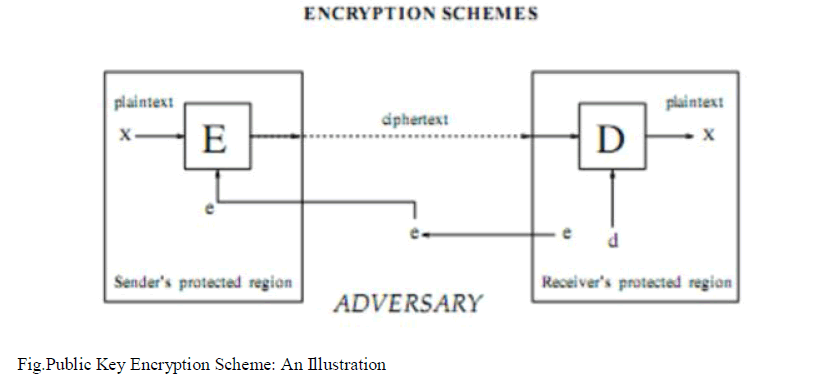
D. RSA Public-Key Cryptographic Algorithm

RSA public-key cryptosystem was named after its inventor, R. Rivest, A. Shamir and L. Adleman. So far, RSA is the most widely used in public-key cryptosystem. Its security depends on the fact of number theory in which the factorization of big integer is very difficult. In the RSA algorithm, key-pair (e, d) is generated by the receiver, who posts the encryption-key e on a public media, while keeping the decryption-key d secret.

E.Homomorphic Encryption and Decryption Scheme

A cryptosystem is homomorphic with respect to some operation ∗ on the message space if there is a corresponding operation ∗′ on the cipher text space such that∗′′ =∗′ . In this section, it is proposed an additively homomorphic encryption and the decryption scheme, which is given follows:

Encryption Algorithm :

1) The algorithm uses a large number, such that = ×, where and are large security prime numbers.

2) Given X, which is a plaintext message, the encrypted value is computed:

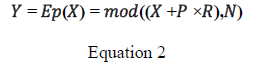Decryption Algorithm

Given y, which is a cipher text message, we use the security key p to recover plaintext

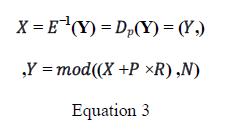Permutation Mapping Table :For a sequence1,2,…,Ã¯Â¿Â½Ã¯Â¿Â½, every value is relatively compared with other values of the sequence and if the result is equal or greater than zero the result will be +1 otherwise will be -1 as shown in Table 1, e.g if1-2>= 0 the value in the mapping table is +1 otherwise is -1. So the permutation mapping table of the sequence1,2,…,4 will be as follows:

The weight for any element in the sequence relative to the others is the algebraic sum of the row corresponding to that element.

III.PROPOSED WORK

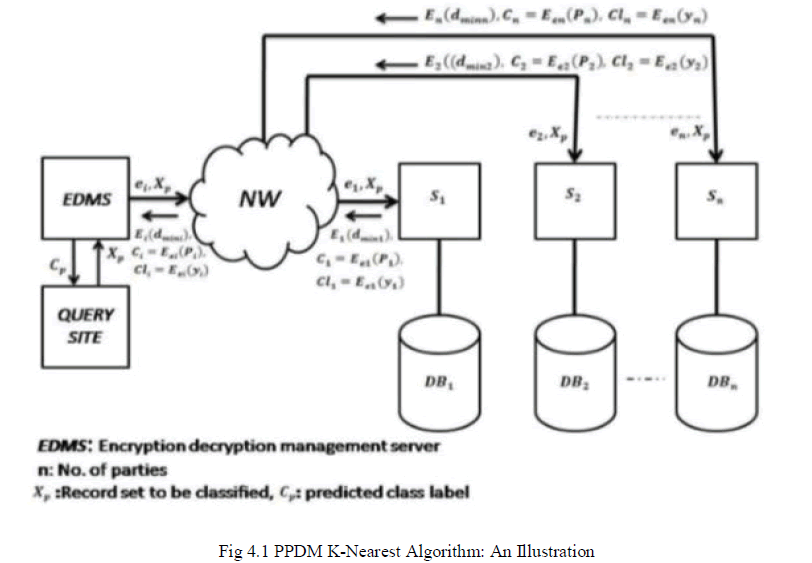
1- In this paper, a semi-honest model for adversary is used, where each party follows correctly the protocol of secure computing function but curiously try to infer data about other parties. A key outcome which is also used in this work is the composition theorem. Now I state it for the semi-honest model. Theorem (1): “Suppose that g is privately reducible to f and that there exists a protocol for privately computing the f. Then there exists a protocol for the privately computing g”. Roughly speaking the composition theorem states if a protocol consists of several sub-protocols, and can be shown to be secure other than the invocations of the subprotocols, if the sub-protocols are themselves secure, then the protocol itself is also secure. A detailed discussion of this theorem, and the proof, can be found in. 2- The proposed algorithm presents a method for privately computing data mining process from distributed sources without disclosing any information about the sources or their data except that revealed by final classification result. The proposed algorithm develops a solution for privacy–preserving k-nearest neighbour classification which is one of the commonly used data mining tasks. The proposed algorithm determines which of the local results are the closest by identifying the class of minimum weight using K nearest neighbours. We assume that attributes of the instance needed for classification are not private (the privacy of the query instance is not protected). Therefore, it is necessary to protect the privacy of the data sources i.e. a site / partyis not allowed to learn anything about any of the data of the other parties and it is trusted not to collude with other parties to reveal information about the data. 3- The idea of the proposed algorithm is based on finding K-nearest neighbours of each site, then scramble and encrypts the local with homomorphic encryption and its class Ã¯Â¿Â½Ã¯Â¿Â½Ã¯Â¿Â½Ã¯Â¿Â½ with the public key Ã¯Â¿Â½Ã¯Â¿Â½Ã¯Â¿Â½Ã¯Â¿Â½ sent from Encryption Decryption Management Server (EDMS). The results from all sites are combined to produce the permutation table at EDMS and instance with minimum weight with its class is determined as the class of querying instance which is transferred to querying site. Each site learns nothing about other sites. Since the KNN algorithm executed locally for each site.

The standard data mining algorithm is K nearest neighbour for each site / party will be as follows:

1- Determine the parameter K= number of nearest neighbors beforehand.

2- Calculate the distance between the query instance and all the training samples using Euclidean distance algorithm.

3- Sort the distances for all the training samples and determine the nearest neighbor based on the Kth minimum distances.

4- Since this supervised learning, get all the classes of training data for the sorted value which falls under K.

5- Use the majority of nearest neighbor as the prediction value.

Notations: (Ã¯Â¿Â½Ã¯Â¿Â½) means to encrypt data x using a special encryption algorithm E. Ã¯Â¿Â½Ã¯Â¿Â½Ã¯Â¿Â½Ã¯Â¿Â½ (Ã¯Â¿Â½Ã¯Â¿Â½); refers to encrypting data x using a special algorithm E with a specified key k.

IV DISCUSSIONS

The purpose of privacy-preserving data mining is to discover accurate, useful and potential patterns and rules and predict classification without precise access to the original data. Therefore, evaluating a privacy-preserving data mining algorithm often requires three key indicators, such as privacy (security), accuracy and efficiency.

Privacy: In the proposed PPDM algorithm, cryptogram management at different levels was adopted. • First, Party encrypts with homomorphic encryption, and is a random number within (1, Ã¯Â¿Â½Ã¯Â¿Â½Ã¯Â¿Â½Ã¯Â¿Â½) ,used as digital envelope for .

Since RSA public key encryption is semantically secure; hence, each party is semantically secure where no party can learn about private data of other parties except its input and the final result. As privacy is preserved for each party, applying the composition theorem (theorem 1), then the total proposed PPDM algorithm is secured. Accuracy: EDMS, which decrypts, (dimin) and its class label cipher () , and produce accurate results with RAS and homomorphic cryptosystem. As shown in tables 3, 4, and 5, the accuracy of the classifier for parties between 2 to 6 is 73.6 – 94.5 % which is comparable to accuracy of classical approach. As in Fig. 5.1 the accuracy is varied according to data set size and number of parties but accuracy range is still accepted and as long as the number of parties increases the accuracy is better.

Efficiency: Raising efficiency of the algorithm is mainly shown the decreases in time complexity. PPDM-KNN algorithm reduces the time complexity mainly in two aspects.

• First: global K-distances are quickly generated, since the KNN algorithm executed locally for every site Ã¯Â¿Â½Ã¯Â¿Â½Ã¯Â¿Â½Ã¯Â¿Â½, this enables solutions where the communication cost is independent of the size of the database and greatly cut down communication costs comparing with centralized data mining which needs to transfer all data into warehouse data to perform data mining algorithm.

• Second: Sitenly have to encrypt encryption paramete of homomorphic encryption system and class labe with public key of RSA. So, the algorithm avoids numerous exponent operations and improves the speed of operation greatly. Tables 3, 4, and 5 shows that the maximum performance time is 1222 ms for training set of size 6000 records.

These results show that privacy of the data sources is preserved while there is no information loss with accurate results.

V CONCLUSION

In this paper, a privacy-preserving distributed KNN mining algorithm has been presented. As demonstrated, the proposed algorithm is based on the technology homomorphism and RSA encryption which is semantically secured. Moreover, no global computations at the centralized site are conducted but the KNN algorithm is computed locally for each site and local results are transferred to the centralized site to be compared. Experimental results show that PPDM has good capability of privacy preserving, accuracy and efficiency, and relatively comparable to classical approach.

ACKNOWLEDGMENT

Every orientation works has an imprint of many people and it becomes our duty to express deep gratitude for the same. During the entire duration of preparation for this Dissertation, We received endless help from a number of people and feel that this report would be incomplete if I do not convey graceful thanks to them. This acknowledgement is a humble attempt to thanks all those who were involved in the project work and were of immense help to me. First and foremost We take the opportunity to extend my deep heartfelt gratitude to the Almighty Allah without whose care and blessing this work would have not completed. We also humbly thank Prof. MandarKhsirsagar, PG Coordinator, Department of Computer Engineering, VACOE, and Ahmednagar for his indispensable support, his priceless suggestions and for his valuable time.

References

A. Inan, Y. Saygin, Privacy-preserving spatio-temporal clustering on horizontally partitioned data, Proceedings of DAWAK06, 8th International Conference on Data Warehousing and Knowledge Discovery, 2006.
M. J. Atallah, F. Kerschbaum, W. Du, Secure and Private Sequence Comparisons, Proceedings of the 2003 ACM Workshop on Privacy in the Electronic Society (2003) 39-44
M. Klusch, S. Lodi, G. Moro, Distributed Clustering Based on Sampling Local Density Estimates, Proceedings of the Eighteenth International Joint Conference on Artificial Intelligence (2003) 485-490
M. Kantarcioglu, C. Clifton, Privacy-Preserving Distributed Mining of Association Rules on Horizontally Partitioned Data, IEEE TKDE, 16(9)(2004)
J. Vaidya, C. Clifton, Privacy-Preserving K-Means Clustering over Vertically Partitioned Data, Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (2003) 206-215
J. Vaidya, C. Clifton, Privacy Preserving Association Rule Mining in Vertically Partitioned Data, Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (2002) 639-644
Referenced at KDD’99 Classifier Learning Contest: http://www-cse.ucsd.edu/users/elkan/clresults.htm (2006)
R. Agrawal, R. Srikant, Privacy Preserving Data Mining, Proc. of the 2000 ACM SIGMOD Conference on Management of Data (2000) 439-450
S. Merugu, J. Ghosh, Privacy-Preserving Distributed Clustering Using Generative Models, Proceedings of the Third IEEE International Conference on Data Mining (2003) 211-218
S. Jha, L. Kruger , P. McDaniel, Privacy Preserving Clustering, Proceedings of the 10th European Symposium on Research in Computer Security (2005) 397-417
S. R. M. Oliveira, O. R. Zaïane, Achieving Privacy Preservation When Sharing Data for Clustering, Proceedings of the International Workshop on Secure Data Management in a Connected World (2004) 67-82
S. R. M. Oliveira, O. R. Zaïane, Privacy Preserving Clustering By Data Transformation, Proceedings of the 18th Brazilian Symposium on Databases (2003) 304-318
S. R. M. Oliveira, O. R. Zaïane, Privacy Preserving Clustering By Object Similarity-Based Representation and Dimensionality Reduction Transformation, Proceedings of the 2004 ICDM Workshop on Privacy and Security Aspects of Data Mining (2004) 40-46
S. Vassilios, A. Elmagarmid, E. Bertino, Y. Saygin, E. Dasseni, Association Rule Hiding. IEEE Transactions on Knowledge and Data Engineering 4 (16)( 2004)
W. Du, Z. Zhan, Building Decision Tree Classifier on Private Data, Proceedings of the IEEE ICDM Workshop on Privacy, Security and Data Mining (2002) 1-8