ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
P.Sivaraman1, S.Manimaran2, K.Parthiban3, D.Gunapriya4
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The main objective of Dynamic Economic Load Dispatch (DELD) is to reduce the total fuel cost of the generators in system. In this paper Particle Swarm Optimization (PSO) algorithm is used to solve the Dynamic Economic Load Dispatch (DELD) problem. DELD is to list the generating units output as to meet the load demand at minimum fuel cost while satisfying all units and operational constraints. Enhancement in scheduling the unit outputs can show the way to fuel cost saving.
Keywords |
| Dynamic economic load dispatch; particle swarm optimization; ramp rate limit; |
INTRODUCTION |
| Economic load dispatch (ELD) problem is one of the basic issues in power system operation. In essence of optimization and its objective is to reduce the total generation costs of the units while satisfying all the constraints. In conventional lambda-iteration method, base point and participation factors method, lagrangian relation method and the gradient methods are used to solve the ELD [1] . In these conventional methods for solution of ELD problems have essential assumption that is incremental cost curves of the units are monotonically increasing piecewise-linear functions[1]. Unfortunately these assumption may cause these methods are infeasible because of its nonlinear characteristics in practical systems [1]. These nonlinear characteristics of a generator include irregular prohibited zones and cost functions which are non smooth or convex and large-scale generating system these conventional method results in longer solution time [1]. A dynamic programming (DP) method for solving the ELD problem with valve-point effect may cause the dimensions of the ELD problem to become enormously large, therefore it requiring large computational efforts[2]. In order to formulate the numerical methods more convenient for solving ELD problems artificial intelligent techniques , Hopfield neural network[2] are employed to solve ELD problems for units with piecewise quadratic fuel cost functions and prohibited zones constraint . On the other hand, Hopfield model may suffer from excessive numerical iterations, resulting in large calculations [3]. In the past decade, a global optimization technique known as genetic algorithms (GA) or simulated annealing (SA), which is a form of probabilistic heuristic algorithm, have been used to solve the optimization problems. Though the Genetic Algorithm methods have been employed to solve complex optimization problems, in recent study has identified some deficiencies in Genetic Algorithm performance. Particle swarm optimization (PSO) first introduced by Kennedy and Eberhart, is one of the modern heuristic algorithms. The PSO algorithm technique can produce the high-quality solutions with time and stable convergence characteristic than other stochastic methods. Dynamic economic load dispatch is solving the economic load dispatch in every second power variation. ELD solve the load dispatch economically at fixed power demand that is power is not varying in every seconds and DELD is solve the load dispatch economically at varying power demand in every second. |
PROBLEM FORMULATION |
| The ELD is one of the sub problem of unit commitment . It is a nonlinear programming optimization problem. Practically the scheduled combination of units at each specific period of operation are listed, the ELD planning must carry out the optimal generation dispatch among the all operating units to satisfy the system load demand, spinning reserve capacity, and practical operation constraints of generators that include the ramp rate limit and the prohibited operating zone . |
| Objective function |
| The core objective of economic load dispatch (ELD) is to reduce the operating costs or the generation costs of the power system while satisfying the various constraints in the system. The DELD problem is formulated to find the optimal fuel cost of the generators while fulfilling the all load demands and also fulfilling the various equality and inequality constraints. The objective function is to minimize the total generating cost (total cost of the system) subjected to the various constraints of the system. |
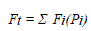 |
| PD = total system demand. |
| PLoss = total transmission line loss. |
| This is called generator constraints. This is also called power balance equation. The transmission loss can be calculated by the B-coefficients method or power flows analysis. B-coefficients used in the power system are |
| Pi=PTB T (6) |
| Where |
| P = Power output of the unit. |
| P = Power output of the unit. |
LEAST PTH NORM ALGORITHM |
| The particle swarm optimization is a population based stochastic optimization technique introduced by James Kennedy and Russel Eberhart in the year of 1995. PSO based on the concept of swarms and their intelligence as well as their movement. PSO comprises of a collection of creatures (particles) performing the same action in a search space. The swarms are mostly the groups that serve the same purpose like food hunting. The PSO is motivated from the relative behaviour of the creatures that live and move in groups like swarm of birds and school of fishes etc. The above figure.1 shows a swarm of birds. This concept is used in PSO algorithm. Here the birds are analogous to the particles. In PSO there is large multidimensional search space with particles within it. These particles are move freely in the search space looking for the optimal (best possible) solution. Each particle has a particular velocity and position. |
| The particles and velocity are denoting by vectors V and X. |
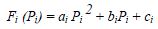 |
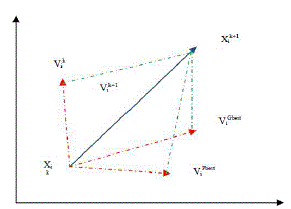
| Every particle represents a potential solution to the problem and they are responsible to search the solutions within the search space. All particles contain a particular fitness value which is evaluated by the fitness function. The velocity and particle position is updated by their rules. The position of the particles is updated with the flying experience of the particle and its neighbours. The best values is achieved by the particles are stored in the memory as Pbest or personal best and the best among all the particles is called as Gbest or global best. By using the concept of Pbest and Gbest the velocity of each particle is updated |
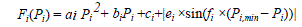 |
| In the equation (7) the inertia weight ω is introduced to enable the swarm to fly in the larger search space. The right value of should be ω selected so as to provide balance between the local and the global explorations. This reduces the iterations to find the optimal solution. |
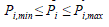 |
| Where |
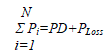 |
| A. PSO Algorithm |
| The step by step procedure of proposed PSO method which is used to solve DELD problem are as given below |
| Step 1: Read the input data such as fuel cost coefficient and the various constraints like as generator constraints and transmission line loss coefficients etc. |
| Step 2: Initialize the population of the particles in random manner. Also set the iteration counter. |
| Step 3: Evaluate the fitness for each particles. |
| Step 4: Now compare the fitness with Pbest and the value of fitness is improved then set this value as Pbest. |
| Step 5: Identify the best fitness value which is Gbest. The best value among the Pbest of all particles is Gbest. |
| Step 6: Update the velocity of each particles. |
| The velocity update rule defined by |
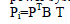 |
| Also, the particles fly to a new position using the position update rule |
| Step 7: If maximum number of iterations reaches then go to |
| step 8, else increase the iteration counter and go to step2. |
| Step 8: The particles that generates the newest best is the solution. This is the optimal solution (result). |
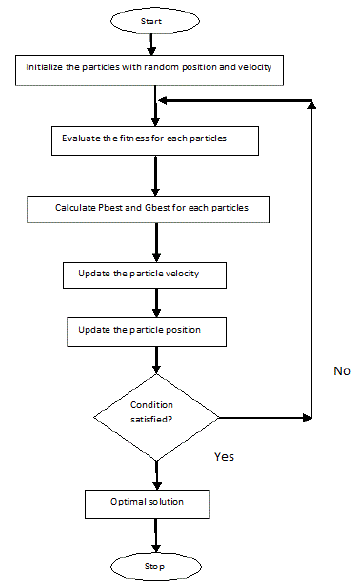
| The above procedure is illustrated in figure 2. |
 |
SIMULATION RESULTS |
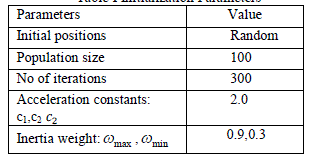
| In this work we have consider a 6 generating units. The load demand is to be allotted to these units while minimizing the costs of generation subjected to the various constraints. Here the constraints like as transmission losses and generators limits are consider. The particles initial position is random and the parameters like as acceleration constants and inertia weight factors, number of iterations and population size are defined. The population size must be set, that it’s not too small or too large. If it’s small there will be inadequate number of particles so there will be difficulty in producing the best possible solution. If the population size is too large then the algorithm will become slow. |
 |
 |
CONCULSION |
| Dynamic Economic load dispatch is a important task in the electrical power system as it is essential to supply the power at the minimum cost. The total generation costs are minimized by dividing the load demand into the several units at the same time it’s satisfying the various constraints. The Load dispatch problem here is solved for the six generating units. The work is done by implementing Particle swarm optimization (PSO) in the MATLAB environment. |
References |
|