International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Quantum Algorithm: A Classical Realization in High-Performance Computing Using MPI

Donald Jefferson Thabah N, Balachandran K, Anirban Roy, & John Kiran A
 Dept of Computer science & Engineering, Christ University Faculty of Engineering, Bangalore, India.
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Quantum computing has been an attractive method adapted for increasing the computational speed and it is governed by the laws of quantum mechanics. Quantum computers are not limited to two states as compared with classical systems, but they encode information as quantum bits or qubits. A qubit represents atoms, ions, photons or electrons and their respective control devices that are working together to act as computer memory and processors. The power of quantum computing lies in its multi-state representation which makes it million times more powerful than classical computer systems. Quantum computers also use another aspect of quantum mechanics known as entanglement, which is a property where multiple objects existing in the states that can be linked together. There exists a standard/specification of message passing library, known as message passing interface (MPI) that can be used for achieving high-performance computing. The goal of MPI is to provide a standardized framework for writing message-passing programs which can be used for programming systems that require distributed processing. The superposition principle used by the quantum algorithm can be simulated in the MPI environment with a cluster of computers or multi-CPU systems. This paper focuses on exposing the strength of quantum algorithm in high performance computing by using MPI, and also on comparing the sequential and parallel execution of programs on the basis of execution time and CPU utilization.

Keywords
qubit, superposition, entanglement, vector space, ket, quantum Fourier transform, Shor’s algorithm, message passing interface.

INTRODUCTION
Numerous non-polynomial hard problems exist in the field of computation which cannot be solved by normal classical computers [1]. A quantum system offers a platform to solve such type of problems [2-3]. Although the miniaturization of computer chips will ultimately result in reducing their dimension to the scale of quantum mechanical prediction, where the mechanisms are governed by the laws of quantum physics, so far, the development of computational machines is still based on the laws of classical physics. A classical computer uses a bit that is set either to 0 or 1, and it does computing using one bit at a time until a program is completed. Whereas, a quantum computer uses a qubit, which is simply a superposition of 0 and 1, and enables each step to run all variations of a bit at the same time, giving them exponentially higher processing power as compared with classical computers. Quantum objects display both particle-like and wave-like features at the same time, and the characteristic property of a wave that is useful in computation is the superposition. This means we will have a “single instruction multiple data” architecture, i.e., having multiple signals at the same position at the same time [4] which will lead to enhanced computational performance of the system.
Recently, there have been reports on work on quantum computing that aims at increasing the computation speed [5-8]. Here we report on our work on gaining speed in computing with specific cases such as factoring huge numbers. While there are different algorithms like Grover’s search algorithm, Simon’s algorithm and Deutsch-Jozsa algorithm [9, 10] for computation, we use Shor’s algorithm which is proved to be one of the best algorithms for finding factors of huge integers [11]. We show a classical simulation of Shor’s quantum algorithm, where the superposition principle is achieved by allocating the states to multiple systems present in a cluster. The execution time and the processor utilization in parallel computing are measured and are compared with those in sequential implementation.

II. QUANTUM COMPUTING
Qubits
The basic unit of information in quantum computation is qubit, which is a quantum bit. Like a bit, a qubit can also be represented in two states labelled as |0> and |1>, and called as a vector or a ket. This notation is very convenient because it expresses that the state of a quantum system is a vector and at the same time denotes the physical quantity of interest (energy level, position, spin, polarization, etc). A qubit can exist in a superposition state, which is a linear combination of |0> and |1>. A qubit can be represented as,
image
where α and β are complex amplitudes, |α|2+|β|2=1, and |α|2 and |β|2 give the probability of finding |ѱ> in |0> or |1> state, respectively. A qubit can also be represented as a vector, for example
image
The vector shown above is in a two dimensional complex vector space and it is normalized to 1 [9-12].
B. Quantum Gates In a quantum computer, information is processed using gates and quantum gates are unitary operators which are reversible [13]. A unitary operator U is the one where the adjoint is equal to the inverse, meaning U†=U-1 (3) In addition, if H is Hermitian operator, then U=eiHt is unitary. A quantum gate with n inputs and n outputs can be represented by a matrix of degree 2n. C. Operator An operator is a mathematical rule that can be applied to a function to transform it into another function. For instance, an operator is applied to a ket |ѱ> to transform it into another ket |∅>. E.g., A|ѱ>=|∅> where A is a unitary operator. (4) An operator can also act on bra as well, i.e., <u|A=<v|. The product of ket and bra can be written as |u><v| (outer product), which is also known as the projection operator.
D. Measurement
Measurement is a projection of the state to the standard basis. Given a state | ѱ> in a two dimensional Hilbert space with orthogonal bases (inner product states |0> and |1> is zero) |0> and |1>, the projection of the state |ѱ> to the standard basis |0> or |1> is known as measurement. The probability that a state |ѱ> being projected to |0> or |1> is given by the square of the complex amplitudes associated with states |0> and |1>.
E. Quantum Fourier transform
Quantum Fourier transform (QFT) is a quantum implementation of the discrete Fourier transform. It transforms the n qubit state vector |α>=α0|0>+ α1|1>+∙∙∙∙∙∙∙∙αn|n> into its Fourier transform |β>= β0|0>+ β1|1>+∙∙∙∙∙∙∙∙ βn|n>, and a measurement on |β> will return only one of its n components. The QFT has the following properties:
a. QFT is unitary b. Linear shift c. Period/Wavelength Relationship
These are the properties that are needed to develop the Shor’s algorithm [10]. The discrete quantum Fourier transform can be expressed as a unitary change of basis,
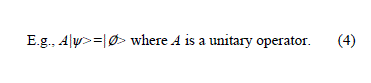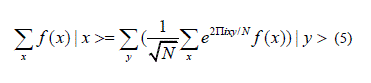image
image
image
Writing integer x and y in a binary notation, e.g. x=xn- 1.2n-1 +…..+x1.2+x0, the non-trivial fractional part of the exponent can be written as Fraction(xy/N)=yn-1(.x0)+yn- 2(.x1x2)+…+y0(.xn-1…x0). Then the unitary rotation of the QFT factorizes as
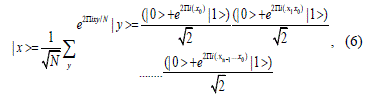image
where the sum over y has been expanded in terms of the two values of each of its n bits. The factorization has converted the sum over N different values of y to a product of n single qubit notation. Complete factorization of the transform provides the maximal O(N/log N) gain for the algorithm. Now the period finding problem requires only one result, i.e., the period from multiple evaluation of f(x), which is possible with maximal quantum superposition of x values and a single run of QFT. This period finding using QFT gains another factor of N/logN in complexity [4, 13].
F. Period/wavelength relationship
Suppose the function f is periodic with a period r. For example see Fig. 1.
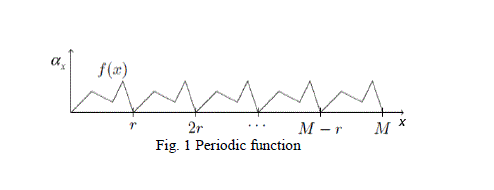image
Then, fˆ (the Fourier transform of f) is supported only on multiples of M/r. Thus fˆ (x) =0 unless x=kM/r. If r is the period of function f, then we can think of M/r as the wavelength of f. The wider the range of function is the sharper the range in the Fourier on the domain, and vice versa. For the Shor's algorithm, the period function is written as
image

III. DEMONSTATION OF SHOR’S ALGORITHM
A. Breaking the RSAencryption RSA (Ron Rivest, Adi Shamir and Leonard Adleman) encryption is based on finite groups, where the group operation is based on multiplication modulo method for some fixed integer N [14]. It is implemented by choosing two huge prime numbers p, q and a large encoding c that has no common factor in common with (p-1)×(q-1). Then inverse can be calculated as cd≡1(mod(p-1)×(q-1)) where d is some integer i.e. c and p×q are known publicly and d is private. Hence to encrypt a message M we perform the operation b≡Mc(mod (p×q)) and to decrypt b we perform the operation M≡bd(mod (p×q)) It can be proved that it is sufficient to decrypt the encrypted message b if we know the order of b. The order r of b divides the order (p-1)×(q-1) of Gpq , and c has no common factor with (p-1)(q-1). Therefore,
image
image
image
image

IV. SIMULATION AND RESULT
We here demonstrate the working of Shor’s algorithm using a simple example of factorizing a number. The simulation was carried out on a cluster of three computers. A. Classical simulation overview 1. Message passing interface (MPI) The message passing interface (MPI) is a library specification for message-passing, proposed as a standard by broadly based committee of vendors, implementors and users [20]. It is designed for high performance computing on both massive parallel machines and on workstation clusters. In this paper, it is implemented on a clusters of workstations. MPICH is a high performance and a widely portable implementation of the MPI standard, and is used here which support of C++.
2. TORQUE Resource Manager TORQUE (Terascale Open-Source Resource and QUEeu Manager) Provides control over bath jobs and distributed computing resources. B. System and Cluster configuration Three systems were used in a cluster, each running CentOS 6.4(Final). The following is the configuration used 1. Master node and two slave nodes. 2. MPICH3 with TOUQUE resource manager were used. 3. All systems have the same configuration with processor Intel(R) Core(TM) i3-2100 CPU @ 3.10GHz and 3Gb RAM.
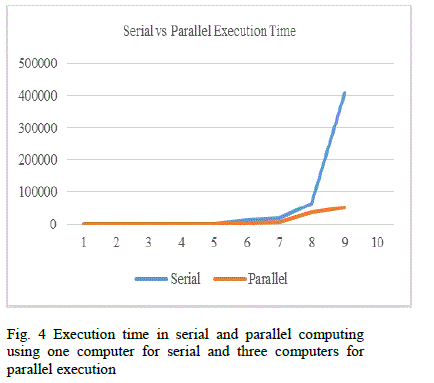
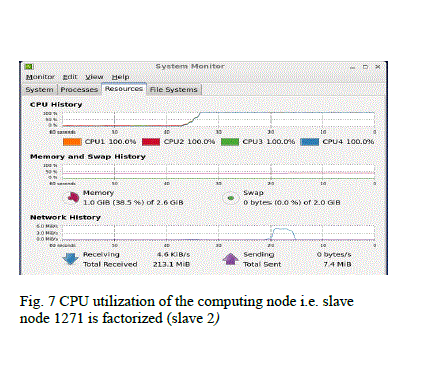
C. Simulation environment We present a realization of Quantum algorithm (Shor’s algorithm) using MPI in a cluster implemented in C++. There are four restrictions for the Shor’s algorithm when it is used for factorizing a number. They are 1. The number to be factorized should be greater than 15 2. The number to be factorized must be odd 3. The number to be factorized must not be a prime power D. Results Table I shows a comparison of the execution time taken by the cluster of computers in parallel and serial mode, respectively, for the chosen problem of factorization of given numbers. It is clear that the time taken in parallel execution is very less, and CPU utilization was 100 % (Figs. 5-7). These results are interesting, showing that quantum computing is able to increase the computational speed.
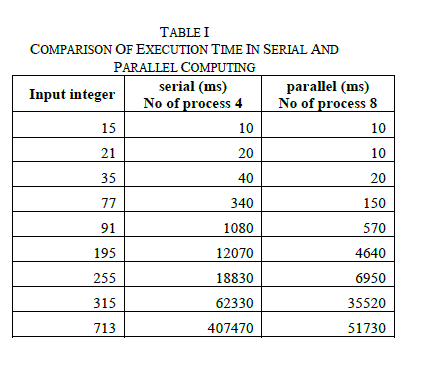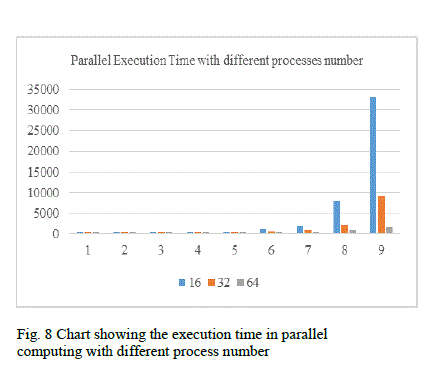image
image
image
image
image
image
Table II demonstrates that by increasing the number of processes in a parallel computing one would achieveThe present work has considered solving factorization problem of integers using Shor’s algorithm. One limitation encountered in this work is the representation of a huge integer by the existing register memory. The future work will consider solving this problem by dividing the quantum states into multiple systems that can represent huge numbers. Shor’s algorithm has been employed by various researchers in solving problem of factoring huge composite integers on different computational platforms like Sun, Enterprise4500 [21, 22]. A direct comparison of our work with the literature report is difficult at the moment due to varying system configurations involved in computation. further increment in speed. Figure 8 graphically represents the processing time taken by the system of three computers for solving factorization problem. It is clear from the table II that the time consumed for factorizing small integers is more in the case of 64 processes, whereas it significantly gets reduced eventually when the integer becomes big, when compared with cases with 16 and 32 processes.

V. CONCLUSIONS
The article demonstrates the simulation of quantum computing using Shor’s algorithm with an example of factorization of given integers. It is found that the parallel computing using a cluster of classical computers is effective in increasing the computational speed. It implies that upon increasing the number of classical systems further in a cluster, one may achieve a better speed for computing.

References
  1. G.A.A. Mary, J.Naresh , C.Chellapan, A Parallel Algorithms for Solving Factorization and Knapsack Problems, IJCSI International Journal of Computer Science Issues, Vol. 9, Issue 2, No 1, March 2012.
  2. M.R.S Aghaei, Z.A Zukarnian, A. Mamat, H. Zainuddin, A Hybrid Architecture Approach for Quantum Algorithm, Journel of Computer Science Vol.5, pp. 725-731,2009.
  3. T.P. Spiller, Quantum Information Processing: Cryptography, Computation, and Teleportation, Proceesings of the IEEE, Vol. 84, No. 12, Dec 1996.
  4. A. Patel, Quantum Computation: Particle and Wave Aspects of Algorithms, Resonance- Journal of Science Education, Vol 16, pp.821-835, 2011.
  5. S. Nakayama, P. Gang, I. Iimura, Study of quantum parallel processing by adiabatic quantum computation in Bernstein- Vazirani problem,13th international conference on parallel and distributed computing application and technologies, China, Dec 12-16, 2012.
  6. D.F.Walls Gerard J. Milburn, Quantum Optics, 2nd Ed., Springer, USA, 2010.
  7. L.M.K. Vandersypen, M. Steffen, G. Breyta, C. S.Yannoni, M. H. Sherwood, I. L. Chuang, Experimental realization of Shor’s quantum factoring algorithm using nuclear magnetic resonance, Nature, Vol 414, pp.883-887, 2001.
  8. G.D. Paparo and M.A Martin-Delgado, Google in a Quantum Network, arXiv:1112.2079v2 [quant-ph], 11 jul 2012.
  9. D. McMahon, Quantum Computing Explained, Wiley- Interscience A John Wiley & Sons, Inc., USA, 2007.
  10. M.A. Nielsen & I.L. Chuang, Quantum Computation and Quantum Information, 10th Anniversary Edition, Cambridge University press, UK, 2010. P.W. Shor, Algorithms for quantum computation:discrete logarithms and factoring, 35th symposium on Foundations of computer science, Santa Fe, pp 124-134, Nov 20-22, 1994.
  11. F. Tabakin, B. Julia-Diaz, QCMPI: A Parallel Environment for quantum computing, arXiv:0902.0699v1 [quant-ph] 4 Feb 2009.
  12. T.P. Spiller, Quantum Information Processing: Cryptography, Computation, and Teleportation, Proceesings of the IEEE, Vol. 84, No. 12, Dec 1996.
  13. W.Zhang, C Xu, F. Li, J. Feng, A Period-finding Methos for Shor’s Algorithm, International Conference on Computational Intelligenc and Security, Harbin, China, 15-19 Dec 2007.
  14. N.D. Merman, Quantum Computer Science an Introduction, Cambridge University press, USA, 2007.
  15. X. FU, W. BAO*, C. ZHOU, Design and Implementation of Quantum Factorization Algorithm, 3rd International Symposium on Intelligent Information Techhnology and Security Informatics, China, Dec 15-19, 2007.
  16. R. Kumar, A. Ranjan and P. Srivastava, An Analytical Optimization Based on Quantum Computing Embedded into Evolutionary Algorithm, 2nd International Conference on Education Technology and Computer (ICETC), China, June 20- 24, 2010.
  17. J.S. Rahhal, Dia I. Abu-AL-Nadi and M. Hawa, Viterbi Decoder Algorithm using Quantum Computing, IEEE Congress on Evolutionary Computation (CEC ), Singapore, Sep 25-28, 2007.
  18. C.P Williams, Explorations in Quantum Computing, 2nd edition, Springer, New York, 2011.
  19. J.L. Traff, W.D. Gropp, R. Thakur, Self-consistent MPI performance guidelines, IEEE Transactions on parellel and distributed systems vol. 21, pp.698-709, 2010.
  20. J.J. Vartiainen, A.O. Niskanen, M. Nakahara, M.M. Salomaa, Implementing Shor’s algorithm on Josephson charge qubits, Vol. A 70, pp. 012319-1-11, Physical Review 2004
  21. C.S. Calude, M.J. Dinneen, F. Peper, Unconventional models of computation, Third International Conference, UMC 2002, Kobe, Japan, Oct 2002