ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
N.SRINIVASA RAO1, K.SRINIVASA RAO2, K.MAHALAKSHMI3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
This paper deals with radio labeling of planar graphs. We proved that a certain class of planar graphs defined using the complete planner graphs, and a class of planar bipartite graphs defined using the complete bipartite graphs are radio labeled properly subject to the certain conditions. We also provide radio labeling for friendship graph
Keywords |
| class of planar graphs, class of bipartite planar graphs, Radio number, Radio labeling. |
| Subject classification: 05C12 |
INTRODUCTION |
| Radio labeling of graphs is motivated by restrictions inherent in assigning channel frequencies for radio transmitters[1].To avoid interference, transmitters that are geographically close must be assigned channel with large frequency difference, transmitters that are further apart may receive channels with relatively close frequencies. The general situation is modeled by identifying transmitters with the vertices of a graph subject to a restriction conenering the distance between the vertices. The goal is to minimize the largest integer used. |
| Definition (1.1): Distance d (u, v) is a shortest path between the vertices u, v in a graph “G”. |
| Definition (1.2): Diameter d(G) is a maximum distance of a graph “G”. |
| Definition (1.3): A Radio labeling is one to one mapping C: v (G) →Z+ satisfying the condition d(u ,v) +âÃâÃâc(u)-c(v) âÃâÃâ≥d(G)+1, for every vertices u, v in G. |
| Definition (1.4): The span of a labeling “C” is the maximum integer maps that “C” maps to a vertex of graph “G”. |
| Definition (1.5): Radio number of graph G, is defined as the lowest span taken over all radio labeling of graph G, and is denoted by rn (G) |
THE CLASS OF PLANAR GRAPHS |
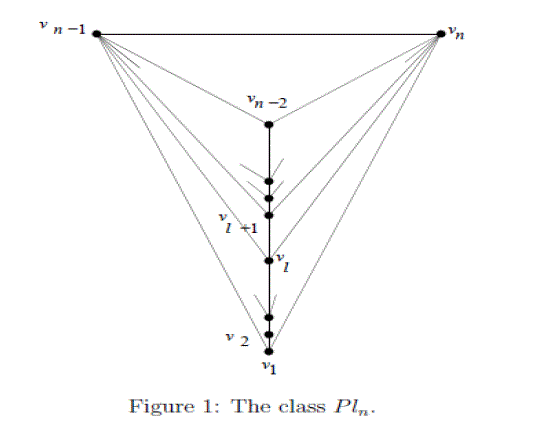
| In [2] Babujee defines a class of planar graphs by removing certain edges from the complete graphs. The class of planar graphs so obtained is denoted by “PL n” and contain maximum number of edges possible in planar graphs on N vertices. |
| Definition (1.6)[ 2]: The class of graphs PL n (V n , En) has the vertex set Vn={1,2,3,..n}, and the edge set En=E (K n)/ {(k, l), 1≤k≤n-4, k+2≤l≤n-2} |
| The embedding we use for Pln is described as follows. Place the vertices v1, v2, ..vn-2 along a vertical line in that order with v1 at the bottom and vn-2 at the top as shown in figure 1.Now place the vertices vn-1 and vn as the end points of a horizontal line segment (perpendicular to The line segment used for placing the other n-2 points) with vn-1 to the left of vn so that the Vertices vn, vn-1 and vn-2 form a triangular face. See figure 1 for an illustration. The edges of the Graph Pln can now be drawn without any crossings. All the faces of this graph are of length 3. From now on, in this section, when we refer to the faces by the vertices of the face, we use the vertex numbers from the embedding described. |
 |
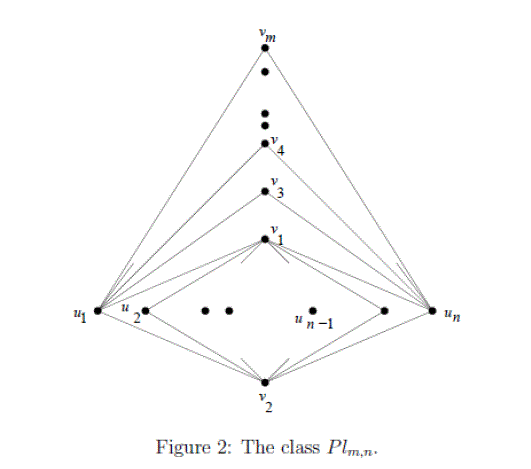
| The class of plm,n of bipartite graphs: |
| Definition (1.7)[3]: the plane (v, E), the vertex set is V = {v1 ,v2,..v m ,u1,u2,..u n} and the set of edges E=E(km,n/{(u l, up): l==3,4,…m, and p=2,3…n-1} The graph is bipartite planner graph with maximum number of edges 2m+2n-4 and m+n vertices. we now describe the embedding we use for our proofs. Place the vertices u1, u2,..u n in that order along a horizontal line segment with u1 as the left end point and un as the right end point as shown in figure2. Place the vertices vm., vm-1,.., v3, v1 in that order along a vertical line segment with v m as the top endpoint and v1 is the bottom end point so that this entire line segment is above the horizontal line segment where the vertices u1through un are placed . finally place v2 below the horizontal line segment so that the vertices v1,uk,v2,uk+1 form a place of length 4 for 1≤k≤n-1. Notice that though we talk about placement along a line segment, no edges other than those mentioned in the definition are to be added. From now on , in this section, when we refer to the faces by listing the vertices forming the face, we use the vertex numbers given by the above embedding. |
 |
RESULTS |
| In this paper, we focused on radio labelling of certain class of planar graphs, planar bipartite graphs and friend ship graphs. |
| Proposition (2.1): The graph pln is Radio labelled where n≥5 |
| Proof: Consider a planar class pln(V, E) with n vertices v1, v2….,vn and 3(n-2) edges. |
| Clearly the distance between the every pair of vertices is ≤2 i.e. d (u ,v)≤2 |
| Diam (G) =2 |
| The labelling of vertices are C(vi)=2i-1 for i=1(2)n |
| Clearly the labelling C (v i) satisfies the radio condition |
| d (u, v)+âÃâÃâC(u)-C(v)âÃâÃâ≥ diam(G) + 1 |
| The class of planar graphs pln(V,E) when n≥5 is Radio labelled. |
| It may be seen that Radio number of class of planar graphs pln(V,E) when n≥5 is 2n-1. |
| Remark: In [1],It is observed that, If G is a connected graph of order “n’’ and diameter 2 then n≤ rn(G)≤2n-2 But we prove that If G is a connected graph of order “n’’ and diameter 2 then |
| n≤ rn(G)≤2n-1. |
| Proposition (2.2): For all m, n≥3. The graph pl m,n is radio labelled, either m is odd or m is even and 4n+m≠0 Proof: consider the planar graph pl m,n with m+n vertices v1, v2….vm, u1,u2,..un and edges 2m+2n-4 edges. Clearly the distance of every pair of vertices is ≤3 i.e. d(u ,v) ≤ 3 |
| Diam (G)=3 |
| The labelling of vertices are C (vi)=2i-1 for i=1to n |
| The labelling of vertices are C (uj)=2(m+j) for j =1 to n |
| Clearly the labelling C(vi) satisfies the radio condition |
| d (u ,v)+âÃâÃâC(u)-C(v)âÃâÃâ≥ diam(G) + 1 where u, v € V |
| Clearly the labelling C(uj) satisfies the radio condition |
| d (u ,v)+âÃâÃâC(u)-C(v)âÃâÃâ≥ diam(G) + 1 where u, v € U |
| In general the distance between the vertices of U, V is ≤ 3. |
| The class of planar bipartite graphs pln(V,E) when n≥5 is Radio labelled. |
| It may be seen that Radio number of class of planar bipartite graphs pln(V,E) when n≥5 is 2(m + j). |
| Friendship graph with 2n+1 vertices and 3n edges: |
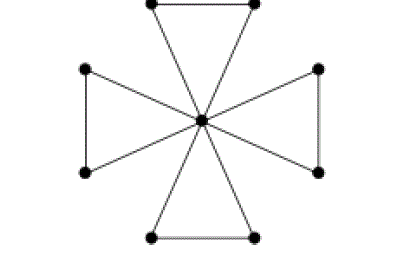 |
| Proposition (2.3): For all n≥1, the friendship graphs are radio labelled properly. |
| Proof: consider the friendship graph Fn with 2 n +1 vertices, and 3n edges. |
| Clearly the distance between the every pair of vertices is ≤2 i.e. d (u, v) ≤2 diam (G) =2 |
| The labelling of vertices are C (vi) = 2i-1 for i=1 to 2n+1. |
| Clearly the labelling C (vi) satisfies the radio condition |
| d (u, v) +âÃâÃâC(u)-C(v)âÃâÃâ≥diam(G) + 1 |
| The class of planar graphs pl n(V, E) when n≥1is Radio labelled. |
| It may be seen that Radio number of friendship graphs Fn where n≥1 is 2i-1. |
| Conclusion: Certain classes f planar graphs are properly Radio labelled in this paper. |
References |
|