International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Recurrent Neural Network Identification: Comparative Study on Nonlinear Process

M.Rajalakshmi1, Dr.S.Jeyadevi2, C.Karthik *3
  1. Department of Electronics & Instrumentation, Kalasalingam University, Tamilnadu, India
  2. Department of Electronics & Instrumentation, Kalasalingam University, Tamilnadu, India.
  3. Kalasalingam University, Electronics & Instrumentation Department, Tamilnadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Neural networks (NNs) have been successfully applied to solve a variety of application problems including nonlinear modelling and identification. The main contribution of this paper is modeling and identification of pH process based on recurrent neural networks. The most powerful types of neural network-based nonlinear autoregressive models, namely, Neural Network Auto-Regressive Moving Average with eXogenous input models (NNARMAX), Neural Network Output Error Models (NNOE) and Neural Network Auto-Regressive model with eXogenous inputs models (NNARX) will be applied comparatively of the pH process identification. Moreover, the evaluation of different nonlinear Neural Network Auto-Regressive models of pH process with various hidden layer nodes is completely discussed. On this basis the features of each identified model of the highly nonlinear pH process have been analyzed and compared. The performance analysis shows that the nonlinear NNARX model yields more performance and higher accuracy than the other nonlinear NNARMAX and NNOE model schemes. The proposed method to identification is not only of the pH process but also of other nonlinear and time-varied parametriic industrial systems.

Keywords
pH process, recurrent neural networks, nonlinear NNARMAX model, nonlinear NNARX model, nonlinear NNOE model, modeling and identification

INTRODUCTION
The system identification field is developed for linear systems. Linear model identification is only useful when physical process exhibits qualitatively similar dynamic behavior of the linear model. All physical systems are nonlinear, so that we need to develop the approaches for nonlinear modelling and analyzing nonlinear systems. The process. The identification and control of pH is important in wastewater treatment and in the chemical industry. But pH is one of the highly nonlinear dynamic system, hence it is difficult to identify and control. It‟s said to be highly nonlinear due to its inherent nonlinearity, the high sensitivity at the neutral point and the time-varying gain (Tre- vathan, 1978; Buchholt and Kummel, 1979; Jutila, 1983). The task of regulating the pH value in an acid–base titration process is a challenging one because the neutralization relationship, the „„S-shape‟‟ curve (McMillan, 1984), has regions of extreme sensitivity and insensitivity. Variations in the titration curve with changes in the field conditions further complicate the control problem. For these reasons, pH control is viewed as an important benchmark for modeling and control of highly nonlinear processes. Among the different nonlinear identification techniques, neural networks (NNs) have been increasingly applied to the identification and control of nonlinear systems. It is one of the most popular identification techniques for highly nonlinear process in industrial applications. In this paper, we propose a method auto-regression recurrent neural networks to obtain an accurate nonlinear system model for pH process. NNs based Modeling techniques have proved to be quite useful for building good quality models from measured data. If such an NN model is available, various control synthesis approaches may be attempted, even if the controllers themselves are not implemented in neural networks.

II. PH PROCESS
The pH process is very important in many industrial applications. It is important to appreciate the diverse nature of these pH control applications because a small amount of acid or base near the set point shows drastic change in pH gain and its characteristics [11]. As shown in Fig. 1, acetic acid is fed to the reactor with a constant flow rate and sodium hydroxide is introduced to the reactor. The mathematical model of the pH neutralization process proposed by McAvoy et al. and reproduced below is used in this work to simulate the pH process. The pH variables used in this study are volume of the continuous stirred tank reactor (V), base flow rate of pH process (���� ), acid flow rate (����) and concentration of acid (Ca) and concentration of base (Cb) [24, 25].
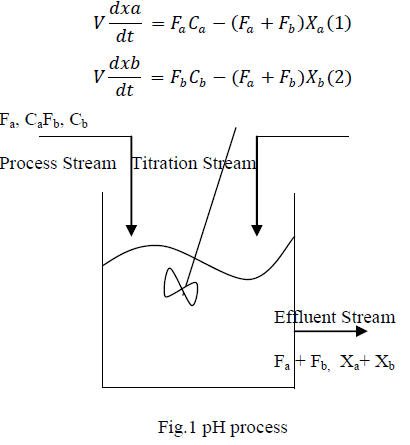image
The above mathematical Eqn. (1) & (2) describe how the concentration of the acidic and basic components, ���� and ���� change dynamically with time subject to the input streams, ����and���� . The relationship can be described by a nonlinear equation known as the titration or characteristics curve. The titration curve varies in two ways discussed as two cases [2]. Case 1:A weak influent is neutralized by a strong reagent Case 2:A strong influent is neutralized by a strong reagent. The word strong and weak is used to characterize the degree of ionic dissociation in an aqueous solution. Strong reagents completely dissociate into their hydrogen or hydroxyl ions whereas weak reagents are only partially ionized [24, 25]. Consider an acetic acid (weak acid) denoted by HAC being neutralized by a strong base NaOH (sodium hydroxide) in water. The reaction between HAC and NaOH:
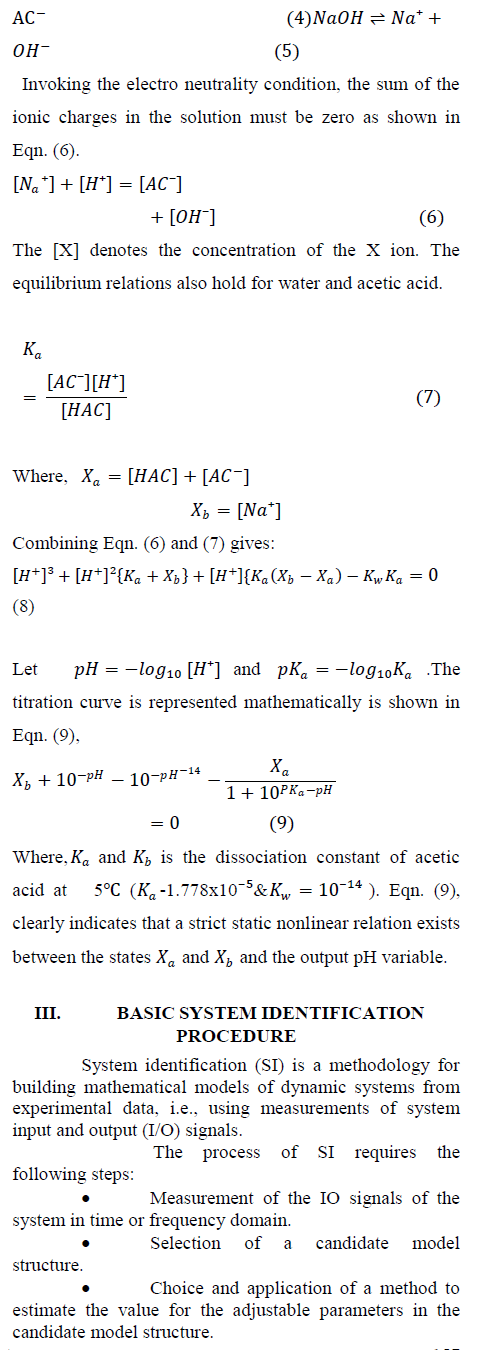image
 Validation and evaluation of the estimated model to see if the model is right for the application needs, preferably with a different set of data. Empirical system modeling generally involves the following aspects [3]. 1. Structure identification or selection:Model structure selection or identification is closely connected to the control objective, i.e. the model must be appropriate for the specific controller design chosen. It must also 2. Reproduce adequately the physical phenomena under consideration, e.g. a Lur'e model is capable of capturing any steady-state behavior, but a Hammerstein model cannot exhibit output multiplicities. Finally, the selected model structure must have an adequate parameterization.
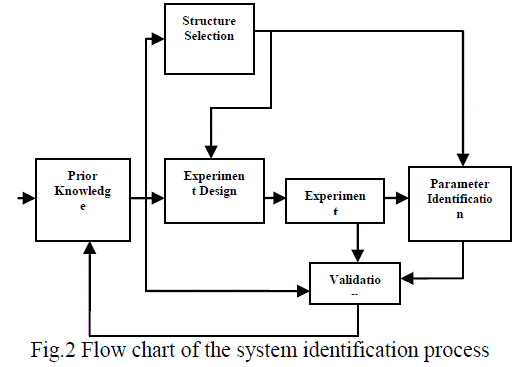image
3. Experiment design- Once a model structure has been selected, the extent to which it provides a reasonable approximation to observed system responses can depend very strongly on the input sequences used to elicit these responses. Thus the input sequences must be chosen to obtain the maximum information about the system behavior. 4. Parameter estimation- Given a model structure and input and output sequences, the goal is to find the model parameters that best correspond to the system behavior. An adequate structure selection is important, because it will determine the possible techniques for parameter estimation, as well as the number of parameters to be estimated.
5. Validation of the final model.

IV. NONLINEAR MODEL STUCTURES BASED ON NEURAL NETWORK
vIn black-box identification of nonlinear dynamic systems, selection of model structures become more difficult task.The multilayer perceptron network (MLP) is most popular for learning nonlinear relationships from a set of data. The following two issues reduced the choice of selecting the model structures.  Selecting the inputs to the network.  Selecting an internal network architecture.
image
Only the NNARX model has a predictor without feedback. The remaining model types all have feedback through the choice of regressors, which in the neural network terminology means that the networks become recurrent: future network inputs will depend on present and past network outputs. This might lead to instability in certain areas of the network‟s operating range and it can be very difficult to determine whether or not the predictor is stable. The ARMAX structure was constructed to avoid this by using a linear MA-filter for filtering past residuals. When a particular model structure has been selected, the next choice which has to be made is the number of past signals used as regressors, i.e., the model order. If no or only very little noise is present (in which case the nnarx function is always preferred). NNARX model structure:
image
For estimating the nonlinear part of the ARX structure, the neural network can be utilized. Multilayer Perceptron (MLP) is one of the popular nonlinear neural network identification structures (M.Norgaard et al, 2000).The neural network version of ARX model structure is denoted as the Neural network ARX (NNARX).The general NNARX model structure is as shown in the following fig.3
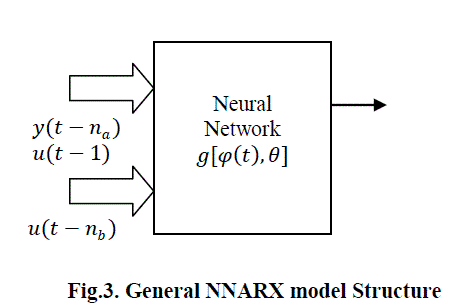image
system. In this case the predictor output is given by Equation 19. �� �� �� = �� �� ��−1 , �� = �� �� �� , �� (19) In this paper, NNARX model structure was selected since it has few advantages over other structures. This model has an algebraic relationship between prediction and past data. The remaining models are containing a feedback from neural output to network input hence they are more complicated (M.Norgaard et al, 2000).To solve the problem of local minima, NNARX model was trained several times and initialization of weights get varied for the starting off each time.

V. RESULTS AND DISCUSSION
The identification process was performed using different recurrent neural network model structures. A total of 3000 data samples are taken which describes the behavior of the pH process[2]. The data set is then divided into 70%for training and 30% for testing data set. Given training data of input-output pairswhere output is “pH of the solution” and input is “Base flow rate”. Figure 4shows the pH of the solution from the selected training and testing data set.
Here the NN regression modelswere applied for divided set data and it shows the modelling of second order nonlinear dynamic system. To select a model structure inside which we wish to search for a good model. The model structure selection consists of two sub problems: choosing a regressor structure and choosing network architecture. For all regressor network architecture 5 hidden 'tanh' units and one linear output unit are chosen.Levenberg-Marquardt algorithm is used for generating a NNARMAX-model,Output Error-model and NNARX-model
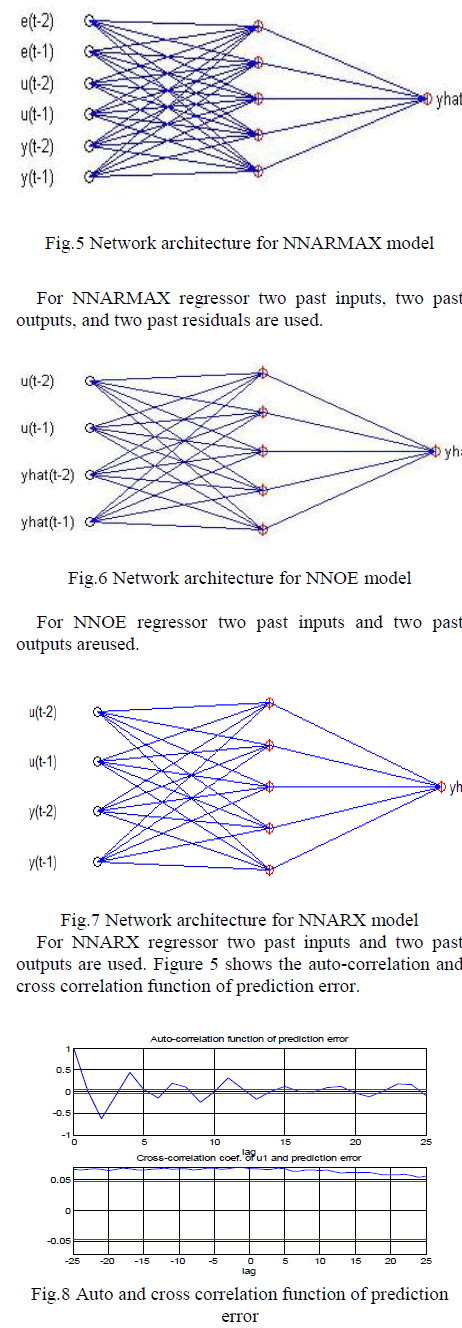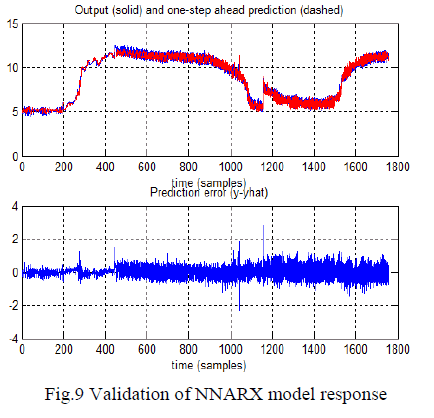image
image
The network has now been trained and validating the model on a fresh data set shown in the fig.9.The NNARX obtained 83.51 fitness which is greater compared to other NN regressors. From previous resulted figures, nonlinear NNARX model always yields more performance and higher accuracy than the other nonlinear models like NNARMAX and NNOE. If we increase the hidden layer nodes from 5 to 10 will improve the performance of neural NNARMAX and NNOE model, except NNARX model because it‟s proved that the hidden layer 5 nodes gives better fitness. Thus, the newly proposed autoregressive neural networks models presented in this study can be applied for the identification of various plants, including linear and nonlinear process without regard greatly changing external environments.

VI. CONCLUSION
In the paper, the model-based identification is discussed with respect to neural networks as universal approximator yielding the possibility of modeling nonlinear autoregressive models with the exogenous variable. Neural networks utilized in modeling and identification of pH process in this paper, have overcome successfully the nonlinear characteristic of the pH process and resulting recurrent neural networks models would surely enhance the control performance of pH process, due to the extraordinary capacity in learning nonlinear characteristic. These results can be applied to model and identify not only of the pH process but also of other nonlinear and time-varied parametric industrial systems.Further work will focus on the design,analysis and implementation of suitable controller for the proposed model.

References
  1. K. Narendra and K. Parthasarathy, “Identification and control of dynamical systems using neural networks,” IEEE Transactions on Neural Networks, vol. 1, pp. 4–27, 1990.
  2. K. Valarmathi, D. Devaraj and T. K. Radhakrishnan. "Intelligent techniques for system Identification and controller tuning in ph process". Brazilian Journal of Chemical Engineering Vol. 26, No. 01, pp. 99 - 111, January - March, 2009
  3. LennartLjung, System Identification - Theory for the User, 2nd Ed, PTR Prentice Hall, Upper Saddle River, N. J. (1999).
  4. L.R. Medsker, L.C. Jain, Recurrent neural networks: design and applications, Boca Raton, FL: CRC Press, 2000.
  5. AlirezaKarbasi, "Comparison of NNARX, ANN and ARIMA Techniques to Poultry Retail Price Forecasting", Thesis, University of Zabol, 2009.
  6. Heba Al-Hiary, Malik Braik, AlaaSheta, and Aladdin Ayesh, "Identification of A Chemical Process Reactor Using Soft Computing Techniques ", IEEE, 2008.
  7. M. Norgaard, O. Ravn, Poulsen, and L. K. Hansen, "Neural Networks for Modelling and Control of Dynamic Systems". Springer, London, 2000.
  8. L.Ricker,http://depts.washington.edu/control/larry/te/download.ht ml,Computers and Chemical Engineering, 1995.
  9. A. K. Jain, J. Mao, and K. K. Mohiuddin, “Artificial neural networks:A tutorial,” IEEE Computer Special Issue on Neural Computing, pp. 31–44,1996.
  10. H.L. Qin and X.B. Li. A chaotic search method for globaloptimization on tent map. Electric Machines and Control,2004, 8(1):67-70.
  11. S R Navghare, Dr. G L Bodhe, Shruti," Design of Adaptive pH Controller using ANFIS", International Journal of Computer Applications (0975 – 8887) Volume 33– No.6, November 2011.
  12. M.Rajalakshmi, C.Karthik "Nonlinear identification of pH process using NNARX model", CiiT International Journal of Artificial Intelligent Systems and Machine Learning, Print: ISSN 0974 – 9667 & Online: ISSN 0974 – 9543, July 2012.
  13. M.Rajalakshmi, C.Karthik “Non Linear Structure Identification Of pH Process” in IEEE - ICAESM 2012, EGS Pillay Engineering college, Nagapattinam, cited by Scopus,ISBN 978-1-4673-0213- 5,Mar 30-31, page 45.