ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| Leo G. Sapogin1, Victor A. Boichenko2 Department of Physics, Technical University (MADI), Leningradsky pr.64, A-319, Moscow, 125319, Russia1 Institute of Control Science Prosoyuznaya 65, Moscow, 117997, Russia2 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The present article discuses the problems of relativistic invariance and commutation relations at unitary quantum theory. The scalar analogue of the main (principal) equation of the unitary quantum theory together with the Poisson equation are solved numerically in this paper. The value of the fine-structure constant, are found, which are in good agreement with the experiment. The evaluation of the electrical form factor of such a particle is also carried out.
Keywords |
||
| Unitary Quantum Theory, Commutation Relation, Relativistic Invariance, Lorentz transformations | ||
INTRODUCTION |
||
| In the standard quantum theory, a micro-particle is described with the help of a wave function with a probabilistic interpretation. This does not follow from the strict mathematical formalism of the nonrelativistic quantum theory, but is simply postulated. A particle is represented as a point that is the source of a field, but can not be reduced to the field itself and nothing can be said about its “structure” except with these vague words. Modern quantum field theory can not even formulate the problem of finding a mass spectrum. | ||
| This dualism is absolutely not satisfactory as the two substances have been introduced, that is, both the points and the fields. Presence of both points and fields at the same time is not satisfactory from general philosophical positions – “razors of Ockama”. Besides that, the presence of the points leads to non-convergences, which are eliminated by various methods, including the introduction of a re-normalization group that is declined by many mathematicians and physicists, for example, P.A.M. Dirac. | ||
| The original idea of Schroedinger was to represent a particle as a wave packet of de Broglie waves. As he wrote in one of his letters, he "was happy for three months" before British mathematician Darwin showed that such packet quickly and steadily dissipates and disappears. So, it turned out that this beautiful and unique idea to represent a particle as a portion of a field is not realizable in the context of wave packets of de Broglie waves. Later, de Broglie tried to save this idea by introducing nonlinearity for the rest of his life, but wasn't able to obtain significant results. It was proved [l], that every wave packet constructed from de Broglie waves with the spectrum a(k) satisfying the condition of Viner-Pely (the condition for the existence of localized wave packets) | ||
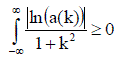 |
||
| becomes blurred in every case. | ||
| There is a school in physics, going back to William Clifford, Albert Einstein, Erwin Schrödinger and Louis de Broglie, where a particle is represented as a cluster or packet of waves in a certain unified field. According to M. JemerâÃâ¬ÃŸs classification, this is a „unitaryâÃâ¬ÃŸ approach. The essence of this paradigm is clearly expressed by Albert EinsteinâÃâ¬ÃŸs own words: «We could regard substance as those areas of space where a field is immense. From this point of view, a thrown stone is an area of immense field intensity moving at the stoneâÃâ¬ÃŸs speed. In such new physics there would be no place for substance and field, since field would be the only reality . . . and the laws of movement would automatically ensue from the laws of field.» | ||
| However, its realization appeared to be possible only in the context of the Unitary Quantum Theory (UQT) within last two decades. It is impressive, that the problem of mass spectrum has been reduced to exact analytical solution of a nonlinear integro-differential equation. In UQT the quantization of particles on masses appears as a subtle consequence of a balance between dispersion and nonlinearity, and the particle represents something like a very little water-ball, the contour of which is the density of energy [11-13]. | ||
| Following, in essence, this general idea, the Unitary Quantum Theory (UQT) represents a particle as a bunched field (cluster) or a packet of partial waves with linear dispersion, and the particle is identified with some field. Dispersion is chosen in such a way that the wave packet would periodically disappear and appear in movement, and the envelope of the process would coincide with de Broglie wave [2-5]. | ||
II.COMMON APPROACH |
||
| Based on this idea, the relativistic-invariant model of such unitary quantum field theory was built [2-5]: a model of the unitary field theory where a particle with mass m is described by the equation | ||
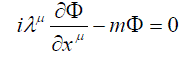 (1) (1) |
||
| and each component ∅s of the wave function satisfies the second order equation | ||
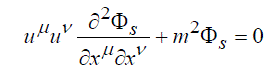 (2) (2) |
||
| so that the commutation relations for matrices λµ have the form | ||
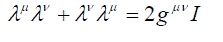 (3) (3) |
||
where 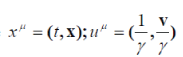 is the particle velocity is the particle velocity 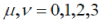 a metrics with signature (+,-,-,-) is used; c and h equal 1, and repeated indices are assumed to be summed. a metrics with signature (+,-,-,-) is used; c and h equal 1, and repeated indices are assumed to be summed. |
||
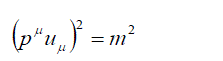 |
||
| Matrices are functions of the particle velocity, and thus the commutation relations (3) alone are insufficient for proving invariance of eq. (1) under the Lorentz transformations; therefore let us first specify the functional dependence of the matrices on the velocity. Since the trivial solution | ||
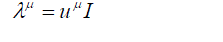 |
||
| is totally uninteresting, let us consider the case of linear dependence on the velocity | ||
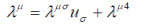 (4) (4) |
||
where 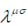 and and 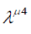 are numerical matrices. The condition (3) holds identically if are numerical matrices. The condition (3) holds identically if |
||
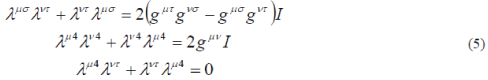 |
||
Because of the antisymmetry of 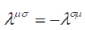 only ten out of the twenty matrices are independent quantities. These matrices mutually anticommute, the square of four of them is equal to unity and that of six, to minus unity. To put it differently, eq. (5) is specified by ten generatrices of the alternion algebra 11 4 A , which is isomorphous with the algebra of the sixteenth order quaternion matrices [22]. Since they are not convenient, let us replace the quaternion matrices with ten complex, irreducible, unitary 32nd order matrices only ten out of the twenty matrices are independent quantities. These matrices mutually anticommute, the square of four of them is equal to unity and that of six, to minus unity. To put it differently, eq. (5) is specified by ten generatrices of the alternion algebra 11 4 A , which is isomorphous with the algebra of the sixteenth order quaternion matrices [22]. Since they are not convenient, let us replace the quaternion matrices with ten complex, irreducible, unitary 32nd order matrices |
||
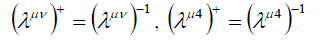 (6) (6) |
||
| This situation arises in construction of Dirac matrices, which are usually chosen as complex fourth order matrices even though the equation | ||
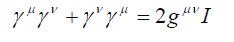 |
||
| is satisfied by four second–order quaternion matrices. | ||
| From eqs. (5) and (6) it follows that four matrices are Hermitian and six are anti-Hermitian | ||
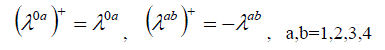 (7) (7) |
||
| If a matrix ïÃÂÃÅ is introduced | ||
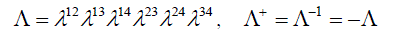 (8) (8) |
||
| then the Hermitian conjugations conditions (7) can be rearranged into | ||
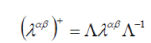 (9) (9) |
||
| Represented in the form (5) the commutation relations are unwieldy and inconvenient in proving the relativistic invariance; however, they can be represented in a simpler form. Let us define a symmetrical tensor gαβ | ||
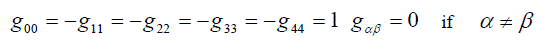 (10) (10) |
||
| henceforth subscripts of initial letters of the Greek alphabet α,β ,γ ,δ take on values from 0 to 4 while those of the middle of the alphabet from 0 to 3. The inverse tensor gα,β provides a compact restatement of commutation relation (5) | ||
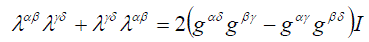 (11) (11) |
||
| Eqs. (4), (10) and (11) make it possible to prove the relativistic invariance of eq. (1) by using a five-dimensional group of transformations of coordinate O (4,1). For this purpose extend eq. (1) to the case of a five-dimensional pseudo-Euclidian space with a metric tensor (10) | ||
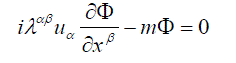 (12) (12) |
||
(where 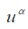 is the 5-velocity, is the 5-velocity, 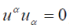 ) and then prove invariance of this equation under the group of fivedimensional transformation O(4,1), which contains the Lorentz group as a subgroup. Under reduction of O (4,1) to the Lorentz group, we assume that ) and then prove invariance of this equation under the group of fivedimensional transformation O(4,1), which contains the Lorentz group as a subgroup. Under reduction of O (4,1) to the Lorentz group, we assume that 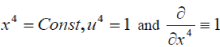 then we have eq. (1); in other words, one can assume that eq. (1) is invariant under five-dimensional transformations, but the physical solution does not depend on the fifth coordinate. Incidentally, eq. (12) can be interpreted differently, but we will not discuss these possibilities, for using the five dimensions is merely a convenient tool, which enables us to make full use of simplicity of the commutation relations (11). then we have eq. (1); in other words, one can assume that eq. (1) is invariant under five-dimensional transformations, but the physical solution does not depend on the fifth coordinate. Incidentally, eq. (12) can be interpreted differently, but we will not discuss these possibilities, for using the five dimensions is merely a convenient tool, which enables us to make full use of simplicity of the commutation relations (11). |
||
| B. The invariance of the equation. | ||
| To prove invariance of the equation, it is sufficient to show [22] that for any transformation of coordinates | ||
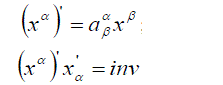 (13) (13) |
||
| there is a linear transformation S(a) of wave functions, the primed and unprimed reference frame | ||
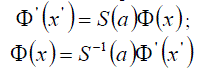 (14) (14) |
||
and  is a solution of the equation, which has the form of eq. (12) in the primed reference frame is a solution of the equation, which has the form of eq. (12) in the primed reference frame |
||
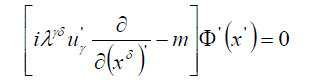 (15) (15) |
||
| Substitute (14) into (12); multiply the left-hand side by S(a), and use the definition (13) to have | ||
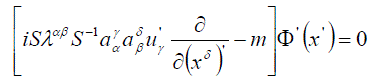 |
||
| This equation coincides with (15), if the matrix has the property | ||
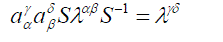 (16) (16) |
||
| Construct S for the infinitesimal proper transformation of the group O (4,1) | ||
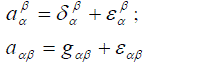 (17) (17) |
||
| with | ||
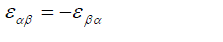 (18) (18) |
||
| Expand S in power of ïÃÂÃÂ¥ and keep only linear terms | ||
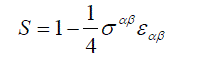 (19) (19) |
||
where 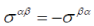 (18). Substitute eqs. (17)-(19) into eq. (16), keep first-order terms in ïÃÂÃÂ¥ , use the notation [B,C]=BC-CB for the commutation brackets and have (18). Substitute eqs. (17)-(19) into eq. (16), keep first-order terms in ïÃÂÃÂ¥ , use the notation [B,C]=BC-CB for the commutation brackets and have |
||
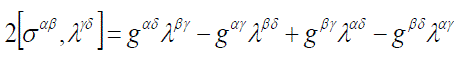 |
||
| The antisymmetric solution of this equation | ||
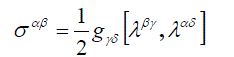 (20) (20) |
||
| is, by virtue of diagonality of the metric tensor and antisymmetry of λαβ a sum of mutually commutating terms; in particular, σ12 has the form | ||
 |
||
| According to eq. (19) S for an infinitesimal transformation is given by | ||
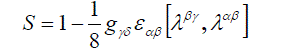 |
||
| Hence, for rotation through a finite angle ïÃÂ÷ about this axis in the direction labeled n is represented as | ||
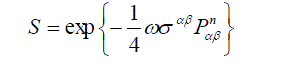 (21) (21) |
||
where 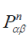 is the generator of rotation about this axis. The matrix S is not, generally speaking, unitary but formula (9) easily shows that is the generator of rotation about this axis. The matrix S is not, generally speaking, unitary but formula (9) easily shows that |
||
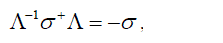 |
||
| consequently, for proper transformations | ||
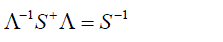 (22) (22) |
||
| Let us consider improper transformations of space reflection and time reversal. For space reflection the matrix a is diagonal | ||
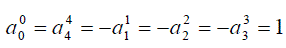 |
||
| then eq. (16) for the space reflection operator P is satisfied by | ||
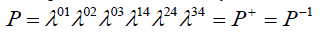 (23) (23) |
||
| which ensures invariance of both eq. (1) and eq. (12). | ||
Construct a transformation of the time inversion; for this purpose introduce an interaction of a particle whose charge is e with an external electromagnetic field 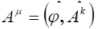 |
||
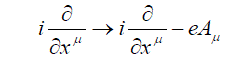 |
||
| and rewrite eq. (1) in the form [2,,3,6] : | ||
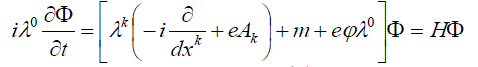 |
||
Determine transformation T as such that if 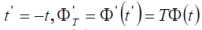 then the latter equation becomes then the latter equation becomes |
||
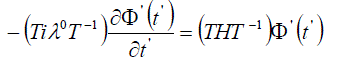 |
||
| When the sense of time is reserved | ||
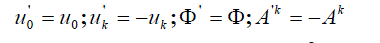 |
||
and, before all, it is necessary to change the sign between two terms 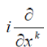 and and 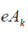 ; therefore the transformation is regarded as a complex conjugation operator multiplied by the matrix T: ; therefore the transformation is regarded as a complex conjugation operator multiplied by the matrix T: |
||
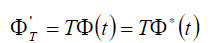 (24) (24) |
||
| This gives | ||
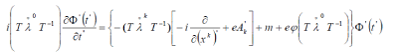 |
||
| and for invariance of the equation it is necessary that | ||
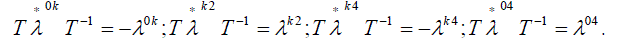 (25) (25) |
||
Thence it immediately follows that  , though the explicit form of the matrix T depends on the particular representation of the matrix , though the explicit form of the matrix T depends on the particular representation of the matrix  . Note that there is just one matrix . Note that there is just one matrix |
||
 |
||
which commutes with both generators 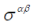 for the representation of the group O (4,1) and with the operators of discrete transformation P and T. Under reduction of O (4,1) to the Lorentz group two more matrices for the representation of the group O (4,1) and with the operators of discrete transformation P and T. Under reduction of O (4,1) to the Lorentz group two more matrices |
||
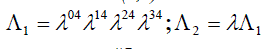 |
||
are generated which commute with the generators 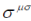 of the representation of the Lorentz group and anticommute with P and T. Consequently, formulae (21), (23)-(25) specify the reducible representation of the Lorentz group and this representation is double-valued. Indeed, consider a particular case, rotation through angle ïÃÂ÷ about the Z-axis. In this case of the representation of the Lorentz group and anticommute with P and T. Consequently, formulae (21), (23)-(25) specify the reducible representation of the Lorentz group and this representation is double-valued. Indeed, consider a particular case, rotation through angle ïÃÂ÷ about the Z-axis. In this case 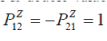 using the explicit form of 12 ïÃÂó we have using the explicit form of 12 ïÃÂó we have |
||
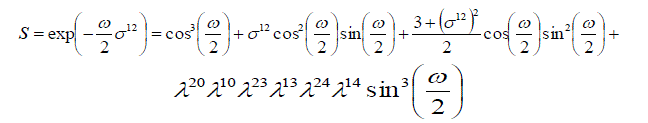 |
||
The half-angle is an expression of the double value of the wave function transformation. Therefore the observables in the theory should be bilinear in ∅(x) The matrix ïÃÂÃÅ makes it possible to determine the adjoint wave function 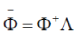 , which is a solution of the adjoint equation , which is a solution of the adjoint equation |
||
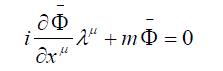 |
||
An adjoint wave function under an arbitrary transformation of the coordinates should be transformed by the equation 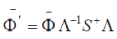 which for proper rotations (22) leads to which for proper rotations (22) leads to 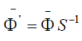 , for space and time inversions , for space and time inversions 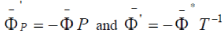 , respectively. The adjoint wave function and the matrices , respectively. The adjoint wave function and the matrices 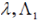 and and 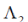 make it possible to construct four independent scalar functions make it possible to construct four independent scalar functions 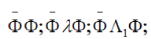 and and 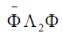 which under space and time inversions are transformed as which under space and time inversions are transformed as |
||
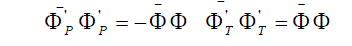 (26a) (26a) |
||
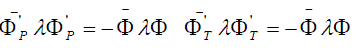 (26b) (26b) |
||
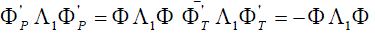 (26c) (26c) |
||
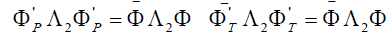 (26d) (26d) |
||
| Following the classification of [20,22], the quantities (26a-d) are singular and simple pseudo-scalar and singular and simple scalar, respectively, each of these functions being a unique scalar function of the associated type, quadratic in ∅(x). To obtain a numerical scalar let us use a representation of the function ∅(x) as a fourdimensional Fourier integral. Since each component of ∅(x) satisfies the second order equation (2), the general solution represented entirely in relativistic terms has the form | ||
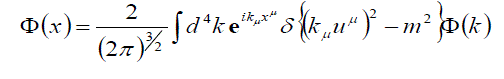 (27) (27) |
||
| where | ||
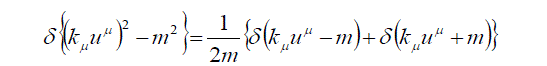 |
||
is the relativistic ïÃÂä -function and the amplitude 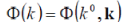 satisfies the equation satisfies the equation |
||
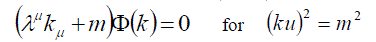 |
||
Because the integrand includes a ïÃÂä -function, the integration is performed over just two Lorentz-invariant hyper surfaces 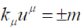 rather than the entire four-dimensional k-space. This allows for decomposing the integral (27) into two summands rather than the entire four-dimensional k-space. This allows for decomposing the integral (27) into two summands |
||
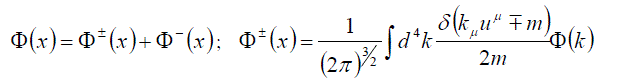 (28) (28) |
||
| Using this representation and integrating over the three-dimensional volume, we have | ||
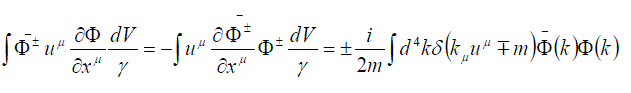 |
||
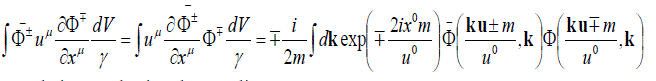 |
||
| Combining these relations and using the equality | ||
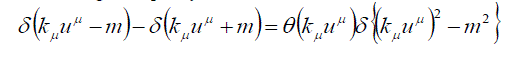 |
||
| we find that | ||
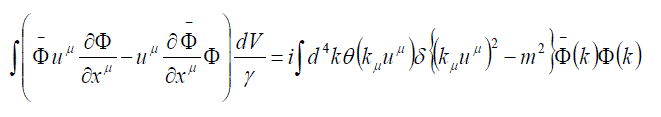 (29) (29) |
||
| where | ||
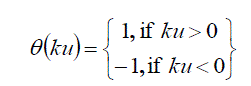 |
||
The right-hand side of eq. (29) is explicitly represented in covariant form, which facilitates a study of properties, which can be traced to the space and time inversions. More specifically, eq. (29) is a simple pseudo-scalar because 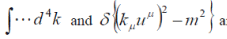 are simple scalars are simple scalars 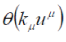 is a singular scalar, (ïÃÂñ is an odd function and ïÃÂàk and ïÃÂàu are simple and singular vectors, respectively), and is a singular scalar, (ïÃÂñ is an odd function and ïÃÂàk and ïÃÂàu are simple and singular vectors, respectively), and 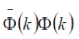 is a singular pseudoscalar, according to the definition (27) and eq. (26a). is a singular pseudoscalar, according to the definition (27) and eq. (26a). |
||
| C. The mass determination | ||
| It is easy to construct a simple scalar | ||
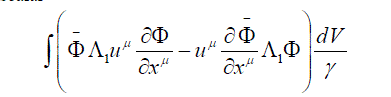 |
||
| which can, following [3,4,6], be interpreted as the particle mass while the nonlinear equation is represented as follows: | ||
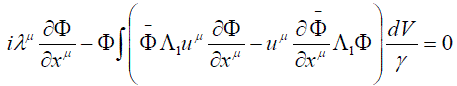 (30) (30) |
||
| Unfortunately, the authors can only look at this fundamental (in our view) equation. It appears that any further progress in finding a solution to such an equation will be achieved with the help of computers and future symbol mathematics programs (of the Maple-16, Mathematica-9 types, etc.). For this purpose equation (30) should have a form with a clear matrix appearance. It is well known that the solution will not depend on a concrete representation of matrices 2 , ïÃÂÊïÃÂàïÃÂì , it is only important that the commutations relations were satisfied. By the way, the latter can be checked by direct finding of commutators and anticommutators with apparent matrix representation. Let us note that the authors of [3,4,6,9-11] had received these results long before the epoch of personal computers and symbol math programs. When these things appeared, the first thing the authors did was to check the correctness of matrix correlations of the size 32ÃâÃâ¦32! | ||
In order to receive a concrete appearance of all the matrices, let us apply the bloc ideas. For this purpose, let us write down the basic matrices 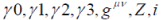 |
||
 |
||
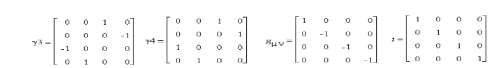 |
||
| For these matrices the following standard commutation relations are correct: | ||
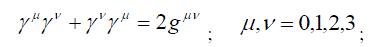 |
||
where 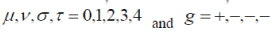 |
||
From these basic matrices 10 supplementary bloc matrices can be constructed 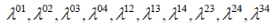 which have a clear appearance: which have a clear appearance: |
||
 |
||
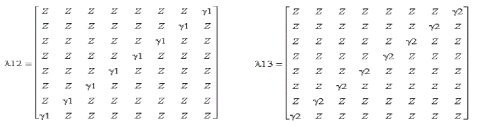 |
||
 |
||
Let us define four-velocity 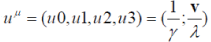 The matrices in the main equation (30) will be defined as: The matrices in the main equation (30) will be defined as: |
||
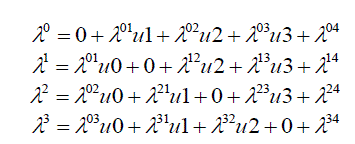 |
||
| The equation then will look as follows: | ||
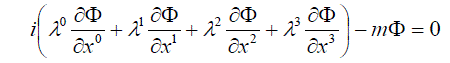 (31) (31) |
||
| The mass term of this equation will then be defined by the following correlation: | ||
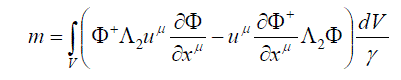 |
||
because 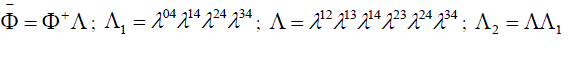 |
||
| The explicit form of 4 matrices ïÃÂàïÃÂì depending on velocity, as well as of numerical matrices 1 2 ïÃÂÃÅ,ïÃÂÃÅ ,ïÃÂÃÅ of the size 32ÃâÃâ¦32. Using a good personal computer it is possible to prove the correctness of the correlations in (5) by making direct computations of the commutators and anticommutators with the help of symbol mathematics programs (Maple -16, Mathematica - 9). | ||
III.SOLVE EQUATIONS |
||
| A. The modified scalar version of the integro-differential equation | ||
| The attempts to solve equation of the (30), (31) type gave no result. However, [10,11,14,15] an interesting was found for a modified scalar version of the integro-differential equation (30), which may be written down as follows: | ||
 (32) (32) |
||
| We will seek the solution of this equation in the form | ||
 |
||
| where | ||
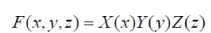 |
||
| and ïÃÂ÷,k are some constant parameters. Substituting these expressions in (32), we obtain under condition ïÃÂ÷ ïÃâ¬Ã½ 3k following equation w.r.t X,Y,Z: | ||
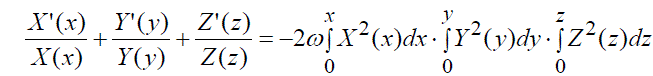 |
||
| Differentiating the left-hand and right-hand sides w.r.t. x,y,z successively, we obtain three equations for X(x),Y(y),Z(z) : | ||
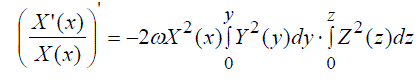 |
||
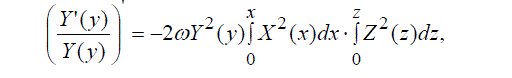 (33) (33) |
||
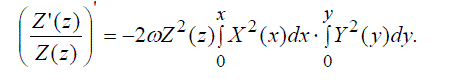 |
||
| Putting | ||
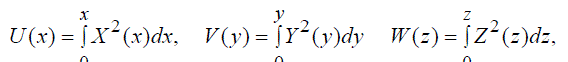 |
||
| we obtain the system of ordinary differential equations for X(x),Y(y),..W. (z): | ||
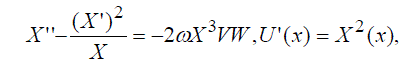 |
||
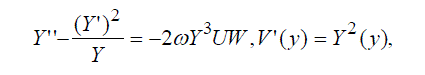 |
||
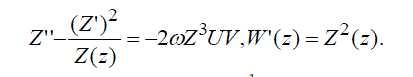 |
||
Further, we have put the numerical value of ïÿýïÿý, namely, 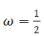 (from behind the oscillation of charge) and integrated numerically (with the help of Maple-16) this system under following initial conditions (reasonable from physical point of view): (from behind the oscillation of charge) and integrated numerically (with the help of Maple-16) this system under following initial conditions (reasonable from physical point of view): |
||
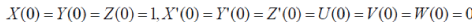 |
||
| According to obtained solution X(x), Y(y), Z(z) are identical rapidly decreasing functions of following type: | ||
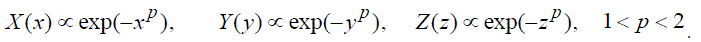 (35) (35) |
||
| The plot of X(x) is shown in Fig.1. | ||
| B. Calculation of dimensionless electrical charge and the value of fine-structure constant. | ||
| The basic equation (32) can be reduced to the scalar equation [7,8] for the density of the space charge of the space charge of the bunch, which represents the particles: | ||
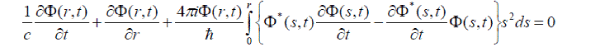 (36) (36) |
||
| Let us solve this equation together with the Poisson equation [6-8]: | ||
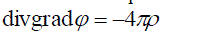 |
||
| We seek the solution in the form | ||
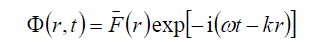 (37) (37) |
||
| We get the following system of equations if the condition | ||
| ω= kc is fulfilled: | ||
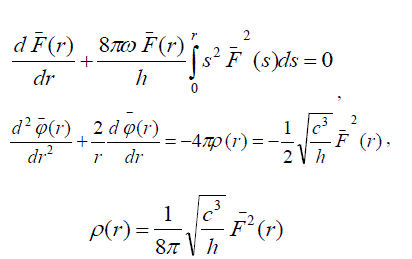 (38) (38) |
||
| where | ||
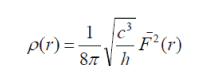 |
||
| is the electrical charge density. Let us suppose | ||
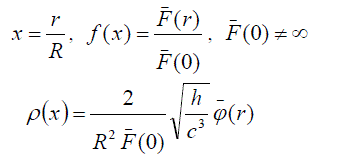 |
||
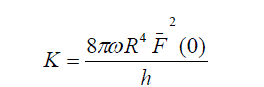 |
||
| System (38) can be expressed in dimensionless form: | ||
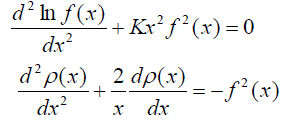 (39) (39) |
||
As long as potential ïÃÂò with the accuracy up to an additive constant and its value does not affect the intensity of electrical field 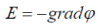 let us choose let us choose 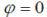 Due to the spherical symmetry in the center of the particle, the condition E = 0 is fulfilled. Solving numerically the Cauchy problem for the system (39), taking the value Due to the spherical symmetry in the center of the particle, the condition E = 0 is fulfilled. Solving numerically the Cauchy problem for the system (39), taking the value 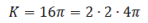 (where (where 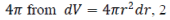 from integral (36) and 2 from charge oscillation) and the initial conditions from integral (36) and 2 from charge oscillation) and the initial conditions |
||
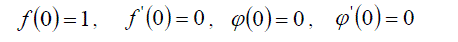 (40) (40) |
||
| we obtain the following integrals | ||
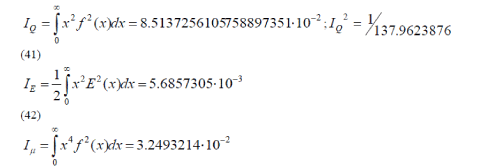 |
||
| The quantity Q I is a dimensionless electrical charge, which is brought to the following dimensional form: | ||
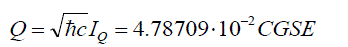 |
||
| This value is less than the modern experimental value of the electron's charge by only 0.3%. This is a fairly accurate number for the first theoretical attempt of the charge calculation. The plot of f(x) is shown in Fig.1. | ||
| Thus it is not unusual to bring out the “corrections” of the J. Schwinger type to the integral (41) | ||
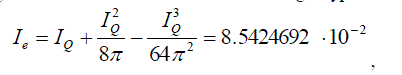 |
||
which corresponds to the value of charge 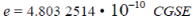 and the value of fine-structure constant and the value of fine-structure constant 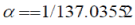 . Calculation spectrum masses some elementary particles see [11-13]. . Calculation spectrum masses some elementary particles see [11-13]. |
||
| The quantization of the electrical charge and masses seems to be the consequence of the balance between the dispersion and nonlinearity, which determines stable solutions. | ||
| The found density distribution for the particle's electrical charge allows us to determine the electrical form factor for the same particle | ||
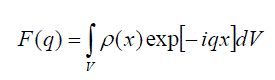 (44) (44) |
||
| We regret that we have not succeeded in finding an analytical solution of eq. (39), but we are able to give a decent approximation. Let us look for a solution of eq. (39) in the form | ||
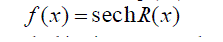 (45) (45) |
||
| Substituting eq. (45) into eq. (39) and taking into account that for small R we have | ||
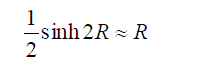 |
||
| we obtain | ||
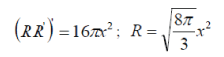 (46) (46) |
||
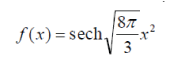 (47) (47) |
||
| It is interesting to note that if the particleâÃâ¬ÃŸs 4-velocity is assumed to be zero at matrix Λ , then system (30) will reduce to eight similar Dirac equations. | ||
IV.PROBLEMS |
||
| A.The Dirac equation | ||
| In our view, although the Dirac equation describes the hydrogen atom spectrum absolutely correctly, it is not properly a fundamental equation. It has two weak points: the correct magnitude of the velocity operatorâÃâ¬ÃŸs proper value is absent. It is known that in any problem of this type the proper value of the velocity operator is always equal to the velocity of light! In fact, Russian physicist and mathematician V.A.Fok regarded this as an essential defect of the Dirac theory. | ||
| The equations of the Unitary Quantum Theory we are proposing are more correct and fundamental. For this reason, a transition from correct fundamental equations to the incompletely accurate Dirac equation needs such a strange requirement as | ||
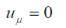 |
||
| However, this requirement is absolutely unsatisfactory both from the physical and the mathematical points of view. Four-velocity has 4 components, of which three are usual components of the particle velocity along three axes, and they really can tend to zero. But the same cannot be done with the fourth component. | ||
| B. The Theories of Aether | ||
| In the second paragraph of the preface of the book A History of the Theories of Aether and Electricity, by Sir Edmund T. Whittaker (Edinburgh, Scotland, April, 1951) was written the following: “A word might be said about the title „Aether and ElectricityâÃâ¬ÃŸ. As everyone knows, the aether played a great part in the physics of the nineteenth century; but in the first decade of the twentieth, chiefly as a result of the failure of attempts to observe the Earth's motion relative to the aether, and the acceptance of the principle that such attempts must always fail, the word 'aether' fell out of favour, and it became customary to refer to the interplanetary spaces as 'vacuous'; the vacuum being conceived as mere emptiness, having no properties except that of propagating electromagnetic waves. But with the development of quantum electrodynamics, the vacuum has come to be regarded as the seat of 'zero-point' oscillations of the electromagnetic field, of the 'zero-point' fluctuations of electric charge and current, and of a 'polarization' corresponding to a dielectric constant different from unity. It seems absurd to retain the name 'vacuum' for an entity so rich in physical properties, and the historical word 'aether' may be fitly retained.” Of course, now aether is not old aether of the nineteenth century. | ||
| The question is that the main relativistic relation between energy, impulse, and mass | ||
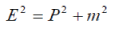 |
||
| has been still beyond any doubt. In particular, all of the previous equations are based on relativistic invariance. Nevertheless, we shall ask ourselves once again about what is happening with that relation at the exact moment when the wave packet disappears being spread over the space. At that moment the particle does not exist as a local formation. This means that in the local sense there is no mass, local impulse, or energy. The particle in that case, within sufficiently small period of time, is essentially non-existent, for it does not interact with anything. Perhaps this is why the relation (48) is average and its use at the wavelength level is equal or less than the De Broglie wavelength, which is just illegal. The direct experimental check of that relation at small distances and short intervals is hardly possible today. If the relation (48) is declined, then it may result in an additional conservation of energy and impulse refusal; but, as we know, according to the Standard Quantum Theory, that relation may be broken within the limits of uncertainty relation. | ||
| C. The LorenzâÃâ¬ÃŸs transformations | ||
| On the other hand, the LorenzâÃâ¬ÃŸs transformations have appeared when the transformation properties of MaxwellâÃâ¬ÃŸs equations were analyzing. However electromagnetic waves derived from solutions of MaxwellâÃâ¬ÃŸs equations move all in vacuum with the same velocity, i.e. are not subjected to dispersion and do not possess relativistic invariance. Our partial waves (may be it is gravitation waves?), which form wave packet identified with a particle, possess always the linear dispersion. Under such circumstances, it would be quite freely for authors to spread the requirement of relativistic invariance to partial waves. Such requirement has sense in respect only to wave packetâÃâ¬ÃŸs envelope, which appears if we observe a moving wave packet and his disappearance and reappearance. May be the origin of relativistic invariance would be connected in future with the fact that an envelope remains fixed in all inertial reference frames; only the waveâÃâ¬ÃŸs length is changed.On the other hand, the LorenzâÃâ¬ÃŸs transformations have appeared when the transformation properties of MaxwellâÃâ¬ÃŸs equations were analyzing. However electromagnetic waves derived from solutions of MaxwellâÃâ¬ÃŸs equations move all in vacuum with the same velocity, i.e. are not subjected to dispersion and do not possess relativistic invariance. Our partial waves (may be it is gravitation waves?), which form wave packet identified with a particle, possess always the linear dispersion. Under such circumstances, it would be quite freely for authors to spread the requirement of relativistic invariance to partial waves. Such requirement has sense in respect only to wave packetâÃâ¬ÃŸs envelope, which appears if we observe a moving wave packet and his disappearance and reappearance. May be the origin of relativistic invariance would be connected in future with the fact that an envelope remains fixed in all inertial reference frames; only the waveâÃâ¬ÃŸs length is changed. | ||
| ItâÃâ¬ÃŸs quite complicated [17-19]. The special relativity – is in fact Lorentz transformations (1904) derived by V.Vogt (1887) in the century before last. These transformations followed from the properties of Maxwell equations which are also proposed in the nineteenth century (1873). One of these equations connecting electrostatic field divergence and electric charge (Gauss' law of flux), in fact is just another mathematical notation of Coulomb's law for point charges. | ||
| But today anybody knows that CoulombâÃâ¬ÃŸs law is valid for fixed point charges only. If charges are frequently moving CoulombâÃâ¬ÃŸs law is not performed. Besides anybody knows that lasers beams are scattered in vacuum one over another, which is absolutely impossible in Maxwell equations. That means that Maxwell equations are approximate - and for the moving point charges experimental results essentially differs from the estimated ones in the case charges areas are overlapping. | ||
| Few people think about the shocking nonsense of presenting in any course of physics of point charge electric field in the form of a certain “sun” with field lines symmetrically coming from the point. But electric field – is a vector, and what for is it directed? The total sum of such vectors is null, isnâÃâ¬ÃŸt it? | ||
| There are no attempts to talk about, but such idealization is not correct. We should note that Sir Isaak Newton did not used term of a point charge at all, but itâÃâ¬ÃŸs ridiculous to think that such simple idea had not come to him! As for Einstein, he considered “electron is a stranger in electrodynamics”. Maxwell equations are not ultimate truth and so we should forget, disavow the common statement about relativist invariance requirement being obligatory “permission” for any future theory. | ||
| To reassure severe critics we should note that UQT is relativistically invariant, it allows to obtain correct correlation between an energy and impulse, mass increases with a rate, as for relativistic invariance just follow of the fact that the envelope of moving packet is quiet in any (including non-inertial) reference systems. To be honest we should note that subwaves the particles consist of are relativistically abnormal, at the same time envelope wave function following from their movement confirms terms of Lorentz transformations. | ||
| D.The spinor quantum electrodynamics. | ||
| The success of Maxwell equations in description of the prior-quantum view of world was very impressing. Its correlation of the classical mechanics in forms of requirement to correspond Lorentz transformations was per fectly confirmed by the experiments that all these had resulted in unreasoned statement of Maxwell equations being an ultimate truth… Other reasons for this were later very carefully investigated by a disciple of one of the authors (L.S.), Professor RatisYu.L. (S.Korolev Samara State Aero-Space University), who has formulated the modern spinor quantum electrodynamics from the UQT point of view: | ||
| 1. Maxwell equations contain constant c, which is interpreted as phase velocity of a plane electromagnetic wave in the vacuum. | ||
| 2. Michelson and Morley have never measured the dependence of the velocity of a plane electromagnetic wave in the vacuum on the reference system velocity as soon plane waves were mathematical abstraction and it was impossible to analyze their properties in the laboratory experiment in principle. | ||
| 3. Electromagnetic waves cannot exist in vacuum by definition. A spatial domain where an electromagnetic wave is spreading – is no longer a vacuum. Once electromagnetic field arises in some spatial region at the same moment such domain acquires new characteristic – it became a material media. And such media possesses special material attributes including power and impulse. | ||
| 4. Since electromagnetic wave while coming through the abstract vacuum (the mathematical vacuum) transforms it in a material media (physical vacuum) it will interact with this media. | ||
| 5. The result of the electromagnetic wave and physical vacuum interaction are compact wave packets, called photons. | ||
| 6. The group velocity of the wave packet (photon) spreading in the media with the normal dispersion is always less its phase velocity. | ||
| All abovementioned allows making unambiguous conclusion: the main difficulties of the modern relativistic quantum theory of the field arise from deeply fallacious presuppositions in its base. The reason for this tragic global error was a tripe substitution of ideas – velocity of electromagnetic wave packets „câÃâ¬ÃŸ being transformed in numerous experiments physics have construed as constant „câÃâ¬ÃŸ appearing in Maxwell equations and Lorentz transformations. Such blind admiration of Maxwell and Einstein geniuses (authors in no case do not doubt in the genius of these persons) had led XX century physics up a blind alley. The way out was in the necessity of revision of the entire fundamental postulates underlying the modern physics. Exactly that was done by UUQFT [14,15]. | ||
| E. The velocity of electromagnetic waves. | ||
| Some time ago CERN has conducted repeated experiments of the neutrino velocity measurement that appeared to be higher than velocity of the light. For UUQFT they were like a balm into the wounds. In fact the movements in excess of the light velocity were discovered earlier by numerous groups of researches. The most interesting were experiments of (Wang, 2000, Princeton, USA), they had disclosed velocities 310 times higher than the light. Nearly everybody disbelieved it. And now the neutrino movements exceeding the velocity of the light were disclosed in CERN. The importance of these experiments for UUQFT is settled in the article [15] where at the page 69 it is written that “this should be considered as direct experimental proof of UUQFT principle”. | ||
| As soon relativistic invariance underlies every of the numerous quantum theories of the field, it leaves a devilish imprint at everything. Nevertheless relativistic ratio between energy and impulse although being absolutely correct in fact are not obligatory follow from relativistic invariance only and can result from another mathematical reasons that will be discovered in future. | ||
| F. The Standard Model and a Higgs boson | ||
| Nowadays Standard Model (SM) combines the most elegant mathematical miracles of researches which hands were tied with relativistic strait-jacket and it not so bad describes these experimental data. Amazing that it was possible to think it out at all. | ||
| Nowadays to confirm SM one should find a Higgs boson and for this purpose the governments of some countries assigned essential sums for the construction of Large Hadron Collider (LHC). For entire SM the interaction with Higgs field is extremely important, as soon without such a field other particles just will not have mass at all, and that till lead into the theory destruction. | ||
| To start with we should note that the Higgs field is material and can be identified with media (aether) as it was in former centuries. But SM authors as well as modern physics have carefully forgotten about it. We would not like to raise here once again the old discussion about it. ItâÃâ¬ÃŸs a quite complicated problem and let us leaves it to the next generation. | ||
| But another problem of SM has never mentioned before: in the interaction with Higgs field any particle obtains mass. As for Higgs boson itself, it is totally falling out of this universal for every particle mechanism of mass generation! And that is not a mere trifle, such “mismatching” being fundamental fraught with certain consequences for SM. | ||
| After Higgs boson discovery nothing valuable for the world will happen except an immense banquet. Of course boson will justify the waste of tens billions of Euros… But even now some opinions in CERN are expressed that probably boson non-disclosure will reveal a series of new breath-taking prospects… and where were these voices before construction, we wonder? But thatâÃâ¬ÃŸs not the point! If this elusive particle were the only weakness of SM! To our regret today this theory cannot compute correctly the masses of elementary particles including the mass of Higgs boson. More worse, that SM contains from 20 to 60 adjusting – arbitrary! - parameters (there are different versions of SM). SM does not have theoretically proved algorithm for spectrum mass computation – and no ideas how to do it! | ||
| All these bear strong resemblance to the situation with Ptolemaic model of Solar system before appearance of KeplerâÃâ¬ÃŸs laws and NewtonâÃâ¬ÃŸs mechanics. This earth-centered model of the planets movement in Solar system at the moment of appearance had required introduction of 40 epicycles, specially selected for the coordination of theoretical forecasts and observations. Its description of planets positions was quite good; but later to increase the forecasts accuracy it had required another 40 additional epicycles… | ||
| Good mathematicians know that epicycles are in fact analogues of Fourier coefficients in moment decomposition in accordance with KeplerâÃâ¬ÃŸs laws; so by adding epicycles the accuracy of the Ptolemaic model can be increased too. However that does not mean that the Ptolemaic model is adequately describing the reality. Quite the contrary… | ||
| The Unitary Quantum Theory allowed computing the mass spectrum of elementary particles without any adjusting parameters. By the way computed spectrum [11-13,16] has particle with mass 131.51711 GeV (L=2, m=2). Once desired it can be called Higgs boson, it lies within declared by the CERN+Tevatron mass interval 125-140 GeV expected to contain Higgs boson. CERN promises to obtain more precise mass value by December 2012. | ||
V.CONCLUSION |
||
| It seems that if UQT were correctly describing the world properties the radical transformation of the civilization would be possible. In conclusion we should express our astonishment that UQT is incomprehensible for any thinking person, itâÃâ¬ÃŸs a mystery to us. We are concluding by reminding of the prophetical words of the famous US science-fiction author Arthur Clarke: “Something that is theoretically possible will be achieved practically independent of technical difficulties. ItâÃâ¬ÃŸs enough to desire it.” (back translation)- Profiles of the Future, 1963. | ||
| We would like to add the amazing phrase of A. de Saint-Exupéry: “The truth is not something that could be proved, but something that makes all things easy and clear” (back translation). | ||
VI.ACKNOWLEDGEMENTS |
||
| The authors thank for discussions to professors A.S.Bogomolv, V.A.Dzhanibekov, V.V.Graboshnikov, P.I.Pospelov, V.M.PrihodâÃâ¬ÃŸko, Yu.A.Ryabov,Yu.P.Savin, V.I.Uchastkin. | ||
Figures at a glance |
||
|
||
References |
||
|