ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Vivek Verma 1, L. K. Yadu 2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Non availability of suitable construction site due to rapid growth of population requires use of low laying areas. Low laying area can be used by suitable structural fill. Well compacted granular fill materials are commonly used to fill the low laying areas. Sometimes, it is required to strengthen the granular fill with some suitable reinforcing materials to increase its bearing capacity. Vertical spacing between reinforcement layers is one of the important geometric parameters which affect the response of the footing resting on granular fill material. In the present study granulated blast furnace slag (GBFS) has been used as granular fill and response of circular footing has been evaluated by varying the vertical spacing of geogrid reinforcement. Response of circular footing obtained in terms of increase in bearing capacity and decrease in the settlement. Vertical spacing of 0.3D has been obtained as optimum and optimum spacing of geogrid reinforcement increases the bearing capacity by 95% and decreases the settlement by 48% as compared to footing resting on unreinforced GBFS bed. Experimental test results were compared with numerical simulation and found reasonable match with experimental results.
Keywords |
| Geogrid reinforcement, bearing capacity, granulated blast furnace slag, circular footing. |
INTRODUCTION |
| Structural fill is required in low laying areas to be use as construction site. Commonly used structural fills are granular materials i.e. conventional aggregate and river sand to fill such sites. In most of the previous studies sand is used as a granular fill [1, 2, 3, 5, 6, 7, 10 and 11] and bearing capacity has been evaluated of the shallow foundation. |
| In this study, Granulated Blast Furnace Slag (GBFS) has been used as granular fill materials to overcome the scarcity of conventional materials in sufficient quantity. GBFS is by-product of steel/iron industries which can be obtained by quenching the slag with water jet. Response of circular footing resting on well compacted unreinforced GBFS bed under transverse loading was evaluated and bearing capacity has been found. Further to increase the bearing capacity, geogrid was used as reinforcement in layers. There are various geometric parameters of reinforcement which affect the bearing capacity of a footing resting on reinforced fill i.e. top layer spacing (u), vertical spacing between reinforcing layers (h), diameter of geogrid layers (a), number of geogrid layers (N), total depth of geogrid layers (d) etc. Vertical spacing is one of the very important parameters, which affect the response of the footing, if others parameter are made constant. In this study, affect of this important parameter was evaluated on the response of circular footing. FEM Package PLAXIS, 2D, 2012 was used to simulate the experimental test results numerically and compared with the experimental results. |
MATERIALS USED IN THE STUDY |
| Granulated Blast furnace Slag (GBFS): Dry GBFS obtained from from Bhilai Steel Plant, Steel Authority of India Ltd, Chhattisgarh, India was used in the study as granular fill material. Properties of GBFS are shown in Table 1. |
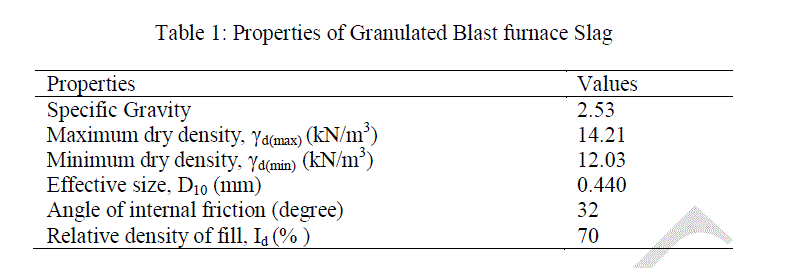 |
| Geogrid: Geogrid made of polyester was used as reinforcement. Properties of geogrid were taken from the manufacturer’s literature. Ultimate tensile strength of geogrid was 30 kN/m. |
EXPERIMENTAL SETUP AND PROGRAMME |
| Circular test tank of 385 mm diameter and 315 mm height was used for performing the experimental test. Rigid circular plate made of mild steel of diameter (D) 100 mm and 12.5 mm thick was used as circular footing. Mechanical jack frame arrangement was used to apply the load manually and measured by pre-calibrated proving ring. Two dial gauges of 0.01 mm least count were used to measure the settlement of the footing due to applied load. Figure 2 shows the pictorial view of the model footing and loading arrangement. |
| Preparation of GBFS beds: GBFS bed was prepared in a test tank at specific relative density by raining technique (Kolbsuzewski, 1948). GBFS were placed in the tank in layers. GBFS were rained from a height of 50 cm to compact the GBFS and with the help of small cans placement density were measured. Placement density were found almost same and 70% relative density was achieved each time. Geogrid layers were placed at the leveled surface. After placing the geogrid layers raining was continued till the desired height. Model footing was placed on the final surface of the GBFS bed. |
| Test Procedure: Test procedure adopted in accordance with Bureau of Indian Standard BIS: 1888 [4]. Load was applied in equal increments and each increment of the load was maintained at least 1 hour and/or until negligible change in the settlement (rate of settlement less than 0.02 mm/min) was observed. Loading was applied until total settlement of the footing attained was at least 12% of footing diameter. |
 |
| Experimental Programme: Test was carried out on unreinforced GBFS bed initially and pressure-settlement behaviour was investigated. Thereafter, tests were carried out on reinforced GBFS bed by varying the vertical spacing of reinforcement. Summary of the test series conducted has been tabulated in Table 2. In reinforced GBFS bed, one particular parameter i.e. vertical spacing was varied, while other parameters were kept constant to understand the effect of parameter on overall response of circular footing. To get the non-dimensional parameter all the geometric parameters were divided by the diameter of the footing i.e. top layer spacing (u/D), total depth of geogrid layers (d/D) and vertical distance between layers (h/D). |
 |
RESULTS AND DISCUSSION |
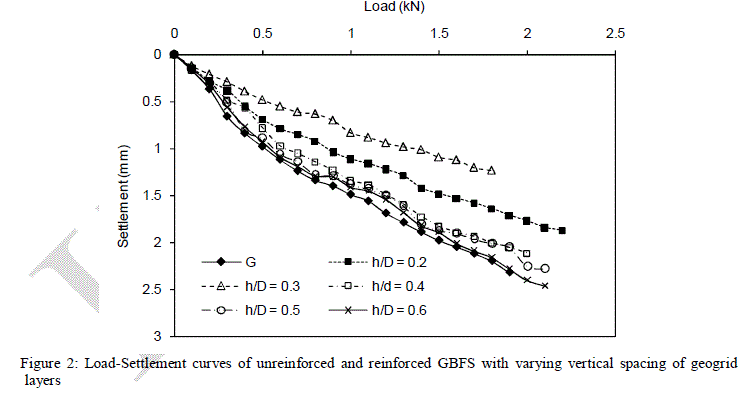
| Load-settlement responses observed from these series of tests are presented in Figures 2. Figure 2 shows the typical variation of load with settlement for the test series G (i.e. unreinforced GBFS bed) and GRh (Reinforced GBFS with varying vertical spacing of geogrid layers). Since, load-settlement curves do not show any marked sign of failure, the approximate ultimate load was determined by log-log plot as proposed by Vesic (1973) [14]. Ultimate bearing capacities were determined by dividing this ultimate load to the footing area. Ultimate baring capacity for all the series of test were found in the similar manner. |
 |
| The increase in ultimate bearing capacity can be expressed in terms of non-dimensional parameter i.e. bearing capacity ratio (BCR) (Binquet and Lee, 1975). The term bearing capacity ratio with respect to the ultimate load is defined as: |
| Where, |
| qu = Ultimate bearing capacity of unreinforced GBFS bed. |
| qu(R) = Ultimate bearing capacity of reinforced GBFS bed. |
| A term Settlement Reduction Ratio (SRR) was used to show the reduction in settlement of footing by reinforcement action. The term is defined as: |
| Where, |
| So = Settlement of unreinforced GBFS bed at ultimate load |
| SR = Settlement of reinforced GBFS bed at same load as So |
| Test Series G: In this series, model test was conducted in the unreinforced GBFS bed. Load-settlement curve for unreinforced GBFS is shown in Figure 2. Based on the load-settlement curve, the experimental ultimate bearing capacity was determined by log-log method [14] and found as 78.9 kN/m2. |
| Test Series GRh: Test series GRh were performed to evaluate the optimum value of vertical spacing between geogrid layers. Figure 2 shows the variation of load with footing settlement for various vertical spacing of geogrid layers. Loadsettlement curve of the unreinforced GBFS is also presented in the Figure 2 to show the performance behaviour of the geogrid reinforcement. It can be clearly seen that as vertical spacing of geogrid layers increases, first load carrying capacity of footing increases, reach to maximum and then decreases. Ultimate bearing capacity were found by dividing the ultimate load to the footing area and listed in Table 3. Bearing capacity ratio (BCR) were found from Equation 1 and presented in Table 3. |
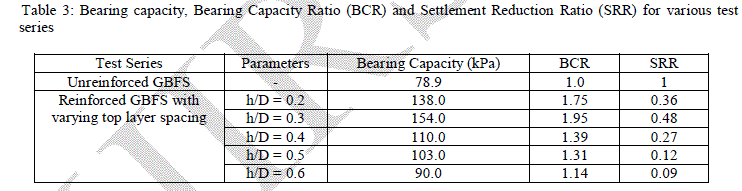 |
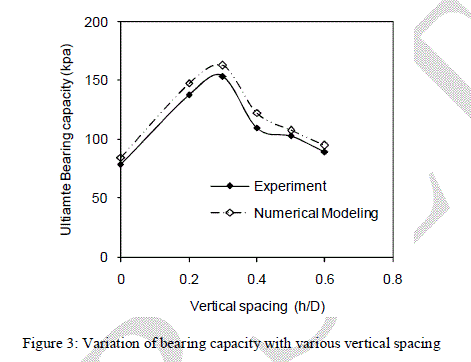
| Variation of ultimate bearing capacity with variation of vertical spacing of geogrid layers is also shown in Figure 4. It can be noticed that ultimate bearing capacity of footing increases from unreinforced GBFS bed (78.9 kN/m2) to 138 kN/m2 for h/B = 0.2 and increases further as 154.0 kN/m2 by increasing the vertical spacing as h/D = 0.3. Thereafter, decrease in ultimate bearing was observed by increasing the vertical spacing. BCR at h/D = 0.3 was observed as 1.95, which shows 95% increase in ultimate bearing capacity as compared to unreinforced GBFS. This increase may be due to the mobilized tension in the reinforcement which enables the geogrid to resist the imposed horizontal shear stresses built up in the soil mass beneath the loaded area and transfer them to adjacent stable layers of soils leading to a wider and deeper failure zone. Further increase of vertical spacing causes the failure of soil in between the geogrid itself. Hence, vertical spacing of 0.3 was adopted as optimum vertical spacing between the layers. SRR were determined by Equation 2 and presented in Table 3. h/D = 0.3 shows 48% reduction in settlement as compared to unreinforced GBFS at ultimate load. |
| Numerical Simulation: PLAXIS software (PLAXIS 2D, 2012) was used to analyze the behaviour of unreinforced and reinforced GBFS bed. The GBFS bed was modeled with Mohr-Coulomb failure criterion. The required five parameters to specify the soil model in Mohr-Coulomb model are secant modulus of elasticity at 50% of strength (Eref), Poisson’s ratio (υ), cohesion (c), angle of internal friction (Φ) and angle of dilatancy of soil (ψ) were obtained from the laboratory test and load-settlement curves of model test. Numerical simulations of the model tests were performed and ultimate load obtained with log-log plot method as proposed by Vesic 1973 [14]. Ultimate bearing capacity was determined by dividing the ultimate load to the footing area. Ultimate load obtained from the numerical simulation were drawn with ultimate bearing capacity of the model test and shown in Figure 3. Figure 3 shows reasonable match of ultimate bearing capacities of various cases obtained by model tests and numerical simulation. |
 |
CONCLUSION |
| In this study, response of circular footing was observed by varying the vertical spacing of geogrid layers. GBFS fill was used as granular fill material. Following conclusions have been derived from this study. |
| Provision of geogrid reinforcement in GBFS improves load carrying capacity and reduces the settlement of the foundation bed substantially. |
| Ultimate bearing capacity of circular footing was observed to be maximum at h/D = 0.30. Ultimate bearing capacity increases by 95% of ultimate bearing capacity of unreinforced GBFS bed, further increase of vertical spacing causes reduction in bearing capacity. |
| Reinforced GBFS bed with two number of geogrid layers provided at h/D = 0.3 decreases the settlement by 48% of unreinforced GBFS bed at its ultimate bearing capacity. |
| Numerical simulation of GBFS bed reasonably matches with the experimental model test results. |
References |
|