ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Tamil Priyadharsini.R1, Sivamurugan.J*2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Reversible data hiding (RDH) in encrypted images, which can recover the original image without any distortion after embedded data is extracted, while protecting the image contents confidentiality. All previous methods embed data by reversibly vacating space from the encrypted images, which may be subject to some errors on data extraction and/or image restoration. Reserving Space before encryption with a traditional Reversible data hiding algorithm, and it is easy for the data hider to reversibly embed data in the encrypted image. The proposed method can achieve real reversibility, that is data extraction and image recovery are free of any error and also embed large payloads for the same image quality as previous method.
Keywords |
| Reversible data hiding ,Encryption, Decryption, histogram,Reserving space before encryption. |
INTRODUCTION |
| Reversible data hiding in images is a technique by which the original cover can be losslessly restored after the embedded information is extracted. RDH is used in medical imagery, military imagery and law forensics, where no distortion of the original cover is allowed. RDH has attracted considerable research interest. Simple and efficient reversible data embedding method for images [1], Tian introduce difference expansion method. Which each group of pixel is expanded .it can be measured by payload capacity limit, visual quality, complexity. It can be used in grayscale image only. The quality degradation on the image after data embedding should be low. An intriguing feature of reversible data embedding is the reversibility, that is, one can remove the embedded data to restore the original image. From the information hiding point of view, reversible data embedding hides some information in a digital image in such a way that an authorized party could decode the hidden information. Hong, Chen [2] established spatial correlation using side match technique to achieve lower error rate. The original work partitions an encrypted image into blocks and each block carries one bit by flipping three LSB a set of pre-defined pixels.Data hiding in images is a technique that embeds data in digital images by altering the pixel values for secret communication, and the embedded image can be recovered to its original state after the extraction of the secret data. It proposes improved data extraction and image recovery strategies based on Zhang’s work better estimate the smoothness of image blocks. An important strategy for RDH is histogram shift [3], in which space is saved for data embedding by shifting the bins of histogram of gray values. Reversible data hiding facilitates immense possibility of applications to link two sets of data in such a way that the cover media can be losslessly recovered after the hidden data have been extracted out, thus providing an additional avenue of handling two different sets of data.The marking techniques satisfying this requirement are referred to as reversible, lossless, distortion-free, data hiding techniques |
| Some reversible marking techniques have been reported. The first method is carried out in the spatial domain. It uses modulo 256 addition to embed the hash value of the original image for authentication. The embedding formula which denotes the original image, the marked image, and the watermark, where denotes the hash function operated on the original image and the secret key. In [4], Thodi and Rodriguez described about Reversible watermarking enables the embedding of useful information in a host signal without any loss of host information.This technique improves the distortion performance at low embedding capacities and mitigates the capacity control problem. Prediction error expansion and histogram shifting combine to form an effective method for data embedding. Two new reversible watermarking algorithms there are histogram shifting and difference expansion. A watermarking algorithms based on the prediction-error expansion technique. A resolution progressive compression scheme which compresses an encrypted image progressively in resolution, such that the decoder can observe a lowresolution version of the image the statistics to decode the next resolution level. Compression of encrypted image [5], in which the typical method is to generate the compressed data in lossless manner. A resolution progressive compression for this problem, which has been shown to have much better coding efficiency and less computational complexity than existing approaches. The success of partial access to the current source at the decoder side to improve the decoder’s learning of the source statistics. |
 |
II. PROPOSED METHOD |
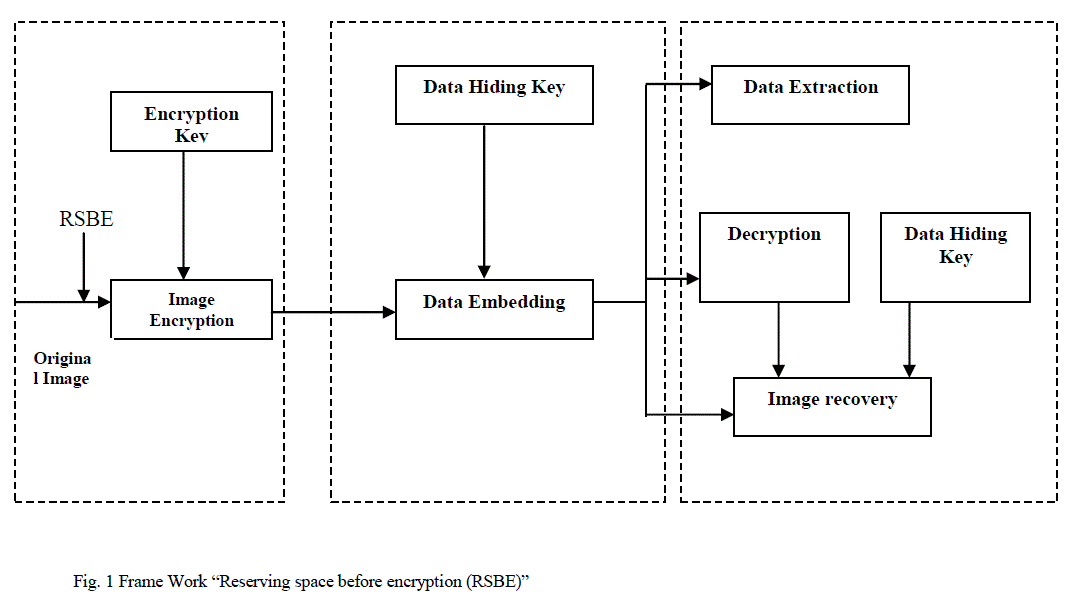
| A novel method for RDH in encrypted images, for which do not “vacate space after encryption” as done but reserve space before encryption”.Vacating space from the encrypted image in relatively difficult and sometimes inefficient, original image will be lost. First empty out space by embedding LSBs of some pixels into other pixels with a traditional RDH method and then encrypt the image, so the positions of these LSBs in the encrypted image can be used to embed data. In Fig.1 RSBE framework, a content owner encrypts the original image using RSAalgorithm.After producing the encrypted image the content owner hands over it to a data hider and the data hider can embed some auxiliary data into the encrypted image by losslessly vacating some space according to a data hiding key. Then a receiver, maybe the content owner himself or an authorized third party can extract the embed data with data hiding key an recover original image from encrypted version according to the encryption key. This process has four steps Generation of encrypted image, Data hiding in encrypted image, Data extraction and image recovery.Reserving space before encryption has provided confidentiality for images. No distortion will be occur during extract the original image from embedded image and also image quality will be good. Real reversibility is realized, that is data extraction and 6image recovery is free of any error. |
| A. Encryption image |
| Construct the encrypted image; the first stage can be divided into three steps: image partition, self reversible embedding followed by image encryption. image partition step divides original image into two parts A and B then, the LSBs of A reversibly embedded into B with a standard RDH algorithm so that LSBs of A can be used for accommodating message then last, encrypt the rearranged image to generate its final version. |
| Image Partition: The reserving space before encryption is a standard RDH technique, The goal of image partition is to construct a smoother area B .To do that, without loss of generality, assume the original image C is an 8 bits grayscale image with its size M×N and pixels ci,j € [0,255], 1≤ i ≤ M , 1≤ i ≤ M. First, the content owner extracts from the original image, along the rows, several overlapping blocks whose number is determined by the size of to-beembedded messages, denoted by l. Every block consists of rows, where, m= [l/N] and the number of blocks can be computed through n=M-m+1. An important point here is that each block is overlapped by pervious and sub sequential blocks along the rows For each block, define a function to measure its firstorder smoothness. |
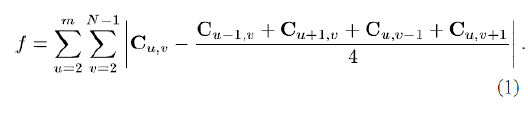 |
| Higher f relates to blocks which contain relatively more complex textures. The content owner selects the particular block with the highest f to be A , and puts it to the front of the image concatenated by the rest part B with fewer textured areas it relies on the fact that only single LSB plane of A is recorded. |
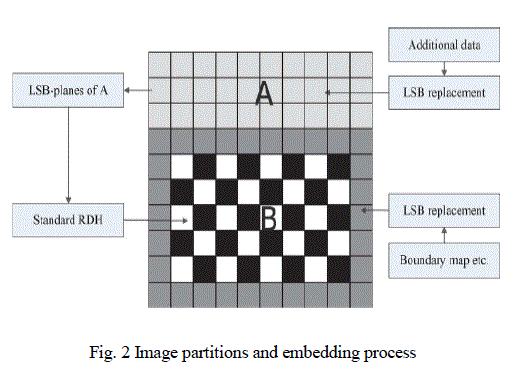 |
| It is straightforward that the content owner can also embed two or more LSB-planes of A in to B, which leads to half, or more than half, reduction in size of A. However, the performance of A in terms of PSNR, after data embedding in the second stage decreases significantly with growing bit-planes exploited. We investigate situations that at most three LSB-planes of A employed and determine the number of bit-plane with regard to different payloads experimentally. 2) Self-Reversible Embedding: The goal of self-reversible embedding is to embed the LSB-planes of A into B by employing traditional RDH algorithms. Pixels in the rest of image are first categorized into two sets: white pixels with its indices i and j satisfying (i+j)mod2 =0 and black pixels whose indices meet (i+j)mod2 =1 as shown in Fig.2.Then, each white pixel, Bij is estimated by the interpolation value obtained with the four black pixels surrounding it as follows |
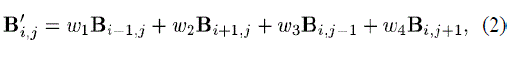 |
| Where, weight wi 1 ≤ i ≤ 4. The estimating error is calculated ei, j = Bi,j -B’i,j and then some data can be embedded into the estimating error sequence with histogram shift. After that, calculate the estimating errors of block pixels with the help of surrounding white pixels that may have been modified.Then another estimating error sequence is generated which can accommodate messages as well. Furthermore, we can also implement multilayer embedding scheme by considering the modified B as “original” one when needed. Bidirectional histogram shift, some messages can be embedded on each error sequence. That is, first divide the histogram of estimating errors into two parts, i.e., the left part and the right part, and search for the highest point in each part, denoted by LM and RM, . For typical images, LM=-1 and RM=0. Furthermore, search for the zero point in each part, denoted by LN and RN .To embed messages into positions with an estimating error that is equal to RM, shift all error values between RM+1 and RN-1 with one step toward right, and then, we can represent the bit 0 with RM and the bit 1 with RM+1.The embedding process in the left part is similar except that the shifting direction is left, and the shift is realized by subtracting 1 from the corresponding pixel values. Fig. 3 illustrates the idea of selecting proper points. Generally speaking, two solutions can gain significantly improvement in terms of PSNR when the length of data is relatively short, i.e., when x = 1. The superiority of one solution over the other depends highly on statistics of natural image. |
 |
| 3) Image Encryption: After rearranged self-embedded image, denoted by c is generated, we can construct the encrypted image, denoted by e.With RSA , the encryption version of e is easily obtained. , It involves different keys for encryption and for Decryption. RSA uses a key length 1024 bits. The first task is to generate a public and private key to do this, choose two large prime numbers and |
| multiply them together. The next step is to choose the Encryption key e and finally compute the Decryption key d such that |
| d=e^-1 mod ((p-1)*(q-1)) |
| The public key constructed from the pair (e, n) and the private key is given by the pair (d, n). The encryption is defined by the formula |
| c= m^e mod n |
| Decryption by |
| m= c^d mod n m → plain text message c → resulting cipher text A larger message is simply treated as the concatenation of multiple 1024 bit blocks. |
| B. Data Hiding in Encrypted Image |
| The data hider acquires the encrypted image c; he can embed some data into it, although he does not get access to the original image. The embedding process starts with locating the encrypted version of A , denoted by Ac. Since AE has been rearranged to the top of c, it is effortless for the data hider to read 10 bits information in LSBs of first 10 encrypted pixels. After knowing how many bit-planes and rows of pixels he can modify, the data hider simply adopts LSB replacement to substitute the available bitplanes with additional data t. Finally, the data hider sets a label following t to point out the end position of embedding process and further encrypts c according to the data hiding key to formulate marked encrypted image denoted by c1 . Anyone who does not possess the data hiding key could not extract the additional data. |
| C. Data Extraction and Image Recovery |
| Data extraction is completely independent from image decryption, the order of them implies two different practical applications. Extracting Data from Decrypted Images: embedding and extraction of the data are manipulated in encrypted domain. On the other hand, there is a different situation that the user wants to decrypt the image first and extracts the data from the decrypted image when it is needed. The following example is an application for such scenario. Assume Alice outsourced her images to a cloud server, and the images are encrypted to protect their contents. The cloud server marks the images by embedding some notation, including the identity of the images, the identity of the cloud server and time stamps, to manage the encrypted images. Note that the cloud server has no right to do any permanent damage to the images. Now an authorized user, Bob who has been shared the encryption key and the data hiding key, downloaded and decrypted the images. Bob hoped to get marked decrypted images, i.e., decrypted images still including the notation, which can be used to trace the source and history of the data. |
| The order of image decryption before/without data extraction is perfectly suitable for this case. The process is essentially similar to that of traditional RDH methods.The following outlines the specific steps: • Step 1. Record and decrypt the LSB-planes A of according to the data hiding key; extract the data until the end label is reached. • Step 2. Extract LN, RN, LM, RM, LP, RP, Rb, x and boundary map from the LSB of marginal area of B. Then, scan to undertake the following steps. • Step 3. If Rb is equal to 0, which means no black pixels participate in embedding process, go to Step 5. • Step 4. Calculate estimating errors e’ i,j of the black pixels B” i, j. If B” i,j If belongs to [1, 254], recover the estimating error and original pixel value in a reverse order and extract embedded bits ei i,j when is equal to LN, LM (or LP),RM (orRP) and RN. Else, B” i,j € {0,254} if refer to the corresponding bit b in boundary map. If b=0, skip this one, else operate like B” i, j € [1, 254]. Repeat this step until the part of payload Rb is extracted. If extracted bits are LSBs of pixels in marginal area, restore them immediately. • Step 5. Calculate estimating errors e’ i,j of the white pixels B” i,j, and extract embedded bits and recover white pixels in the same manner with Step 4. If extracted bits are LSBs of pixels in marginal area, restore them immediately. • Step 6. Continue doing Step 2 to Step 5 x-1 rounds on B” and merge all extracted bits to form LSB-planes of A. Until now, we have perfectly recover B. • Step 7. Replace marked LSB-planes of A with its original bits extracted from B” to get original cover image C. |
 |
III. EXPERIMENTS AND COMPARISONS |
| We take standard image Lena, shown in Fig. 4(a), to demonstrate the feasibility of proposed method. Fig. 4(b) is the encrypted image containing embedded messages and the decrypted version with messages is illustrated in Fig. 4(c). Fig. 4(d) depicts the recovery version which is identical to original image. It compared the proposed method with the state-of the-art works all methods introduce some errors on data extraction and/or image restoration, while the proposed method is free of any error for all kinds of images. The quality of marked decrypted images is compared in the term of PSNR. We modify the methods with error-correcting codes to eliminate errors. In proposed method Rivest, Shamir, Adalman algorithm is used for encryption. |
| The gain in terms of PSNR is significantly high at embedding rate. In addition, another advantage of our approach is the much wider range of embedding rate for acceptable PSNR. In fact, the proposed method can embed more than 10 times as large payloads for the same acceptable PSNR as the method which implies a very good potential for practical applications. |
IV. CONCLUSION |
| Reversible data hiding in encrypted images is an effective method for privacy protection. Previous methods implement RDH in encrypted images by vacating space after encryption. Reserving space prior to encryption method is to provide confidentiality .Thus the data hider can benefit from the extra space emptied out in previous stage to make the data hiding process effortless. The proposed method can take advantage of all traditional RDH techniques for plain images and achieve excellent performance without loss of perfect secrecy, greatly improvement on the quality of decrypted image. |
References |
|