ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
R. Tamijetchelvy, P. Sankaranarayanan, S. Kumudham@Sowdhani, T. Adhithya
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In the recent years of plethora of wireless access environment, there exist hackers for electronic eavesdropping and unauthorized accessing of original data. Hence it is indeed important to secure data, exclusively multimedia data includes image and video which may consist of receptive data in the field of defense, politics etc. A better way to protect the data is using a consistent encryption, making it roughly unfeasible for a third party to access data and to provide essential reliability, privacy and endorsement. In this paper, image encryption on a gray scale is performed based on the pixel by pixel approach and block by block approach. Chaotic system is used for its unique characteristics of initial sensitivity which in turn a small variation in initial condition defer extensively diverging outcomes for dynamical systems making prediction impossible. The Chen, Henon and Lu chaotic system are used for enhancing the security by obliging multi key principles. Simulation results show that the system is resistive against various attacks and proves its excelling efficiency. Finally the proposed system is made to endure geometric cryptanalysis for its prioritized performance.
Keywords |
| Chaos, Pixel, Multi-key, Sensitivity, Dynamic, Encryption. |
INTRODUCTION |
| Cryptography is an indispensable tool for securing the confidentiality of communication and different methods are adapted to encrypt and decrypt data to protect the message. Encryption prevents the invisible modification or deletion of data and regarded as a sign of authentication hat actually resides in the communication systems. Although modern efforts step towards the standardization of algorithms and protocols to make the encryption easier and cheap, many systems fail to meet security. In the broad entity of networked systems, there is a chance for information to be received and misrepresented by adversaries using prominent attacks at diverse levels during the communication [1]. Hence image encryption schemes are performed to organize the required real-time privileged image transmission over the networks and in wireless networks. Traditional encryption algorithms provide less security, high computational complexity and also have low efficiency when the image size is larger [2]. While encrypting a video sequence certain parameters like compression ratio, security and efficiency should be taken into consideration, because any of the factors may result in the deviation of the data. Data encryption standard (DES) proves robust against attacks but the encryption speed is slow and can be cracked easily [3]. The required data can be encrypted by using a compression algorithm like DCT coefficient for more reliability and firmness [4, 5]. Diffie Hellman has been weakened by the man in the middle attack or intruder attack. RSA algorithm is ceased by the encryption speed hence its processing time is high when the information is so long. AES (advanced encryption standard), RC4 and other existing algorithms have their own limitations such as insecurity and less speed thus making unsuitable for most of the real time applications [6]. Hence it paved the way for chaotic system which is an efficient way to deal with the obstinate problem of fast and high security image encryption. Jiri Fridrich [7] proposed an encryption algorithm that adapted certain invertible chaotic two-dimensional symmetric block encryption mapping. This idea is particularly needed for encryption of high amounts of data in digital images. But the system is limited to the two dimensional system and cannot be accomplished for a three dimensional system of complexity [8]. Chaotic mapping and cryptographic algorithms have similar approaches as randomness property whereas the algorithms shamble and distribute data by rounds, while chaotic maps spread a small region through iterations. The main difference between them is that the encryption operations are defined only for finite sets of integers but chaos is definite on real numbers. Chaotic systems are known for its peculiar properties, namely sensitive dependence on initial conditions and parameters, pseudorandom property [9], non transitivity whereas traditional cryptography schemes mainly emphasis on complex arithmetic operations. Li-hui Zhou also suggests that the low-dimensional chaotic system, does not offer high security [10]. Therefore, those chaotic cryptosystems have more practical applications with the advantages of high-level accuracy and plainness when Logistic map has been widely used [11]. While finding the solutions for the numerical values of the differential equations, Lorentz found the sensitiveness which corresponds to the drastic changes in the outcome of the system and constitute an inseparable characteristic of chaotic system. Sobhy and Shehata described a chaotic system using Lorentz algorithmic function for encryption which indicates the time required for encrypting an image requires 20 seconds, which is moderately intolerable for a real time transmission [12, 13]. The rest of the paper is organized as follows: section 2 discusses the proposed multikey image encryption system based on three chaotic systems. Section 3 provides the simulation results and discussion. Then the security analysis and performance of the proposed system are verified in section 4. Analytic experiments are performed for image encryption speed either by block by block and pixel approach. Finally section 5 concludes the results and scope for future aspects. |
II. PROPOSED ROBUSTIC IMAGE ENCRYPTION |
| The proposed robust chaotic image encryption process provides an optimized and efficient way for image security. Many chaotic based image encryption schemes have been proposed for both single key and multi key techniques. The objective of enrichment is to process an image, so that result is more suitable than the original image for the explicit application. In this paper the acquired gray scale image of size 256 × 256 is chosen. The perfection of the system’s stability, the chaotic systems make use of the availability of the Lu, Henon and Chen differential equation in generating an exceptional key as an alternative of using a single key or repeating the identical key after a definite interval of time [14, 15]. Hence the multi-keying principle making it highly unpredictable and enhancing the sophisticated security. Henceforth the key is generated using those equations and process of confusion and diffusion are employed to meet the requirements and to increase the complexity of encryption techniques. Lu equation uses three spatial coordinates (x, y, z) and a single time coordinate t. |
| The equation is a nonlinear system which provides hyper synchronization resulting in diverging outcomes. The initial conditions are specified as a = 36, b = 3, c = 20 and it results in exotic behavioral changes of the chaotic system. Anti-controls of chaos led to the Chen equation which uses non chaotic system particularly the continuous-time three-dimensional autonomous equation with only two quadratic terms. |
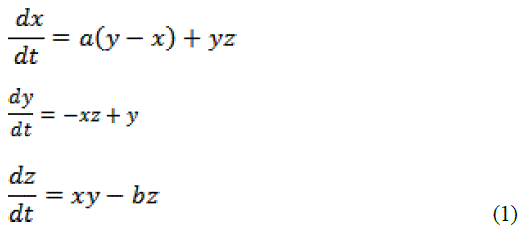 |
| Parameters are a = 35, b = 3, c = 28. The strength of cryptography lies in the way the key is chosen (secret parameters), used in encryption process and the key cannot be guessed by an intruder in the wireless medium. |
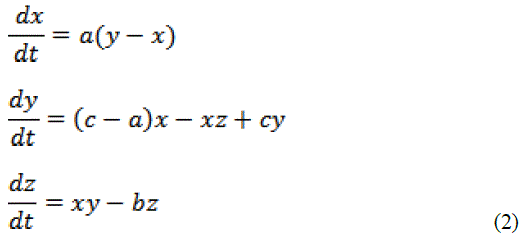 |
| The basic idea behind Henon mapping is that all the set of real values converge at a point. The value of a and b are assigned as a = 1.4 and b = 0.3 to trace the behavioral changes of the system. |
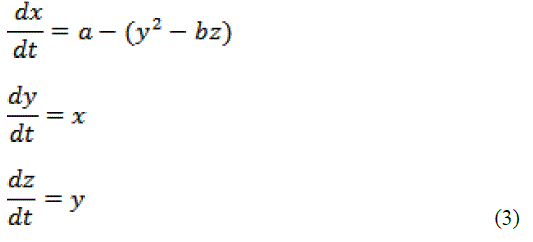 |
| A. Encryption and Decryption Module |
| Initially the gray scale image to be encrypted is taken, the first stage of confusion process is done by either block by block approach or by using pixel by pixel approach. The block by block approach and the pixel by pixel approach are compared with its encryption speed and efficiency. The blocks size can be of 2x2, 8x8, 16x16 and 32x32 to vary its drastic performance. The pixel position confusion is done by multikey chaotic system Chen, Lu and Henon with external 128 bit key [16]. The generated chaotic sequence is used to confuse the pixel position of the grayscale image. The nature of the original image is changed but its spatial characteristics remains as same as the original image. Therefore diffusion process is needed to make the confused image unpredictable. The combined confusion and diffusion process is shown in fig. 1. The decryption process is symmetrical to that of the encryption process. The shuffling can be done randomly by confusing the position of pixels. In the case of decrypting the image by block by block approach the respective blocks are confused for its decryption. The key is generated by using Chen, Lu and Henon mapping with randomness to inhibit with the external key of 128 bits. As a result of sensitivity to initial conditions, the chaotic system enables unpredictable nature as in fig. 2. |
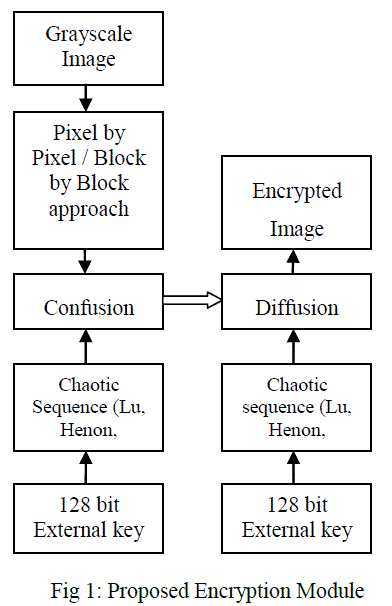 |
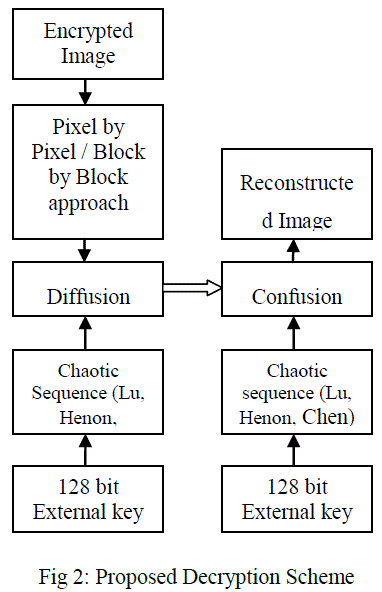 |
| B. Pretreatment Process |
| The system exhibits monotonic characteristics and the mandatory required is pretreatment analysis for the respective sequences. In order to unify the domain values of x, y and z coordinates of the spatial domain the values are rounded off to the nearest values by neglecting the decimal part and real sequence is taken into consideration. Hence uniform distribution and correlated property can be achieved. |
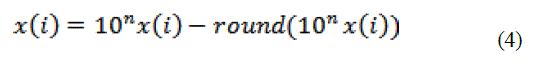 |
III. SIMULATION RESULTS AND DISCUSSION |
| The computational complexity of the encryption algorithm relays mainly on the data volume and the encryption operations. Hence in order to evaluate the performance, a brief comparison is made between the pixel by pixel approach and block by block approach. This section provides the experimental results and analysis to explain how the performance of the proposed cryptosystem is improved using multi key concept [16]. The test grayscale image taken for encryption is of size 256 ÃâÃ⦠256, its corresponding histogram analysis is depicted and illustrated in fig. 3. |
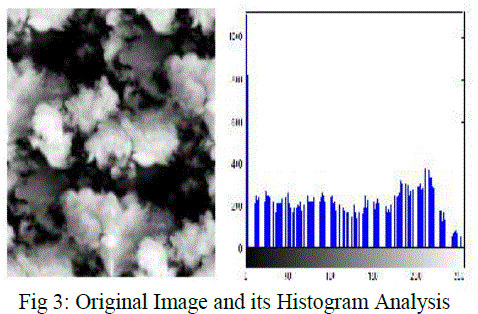 |
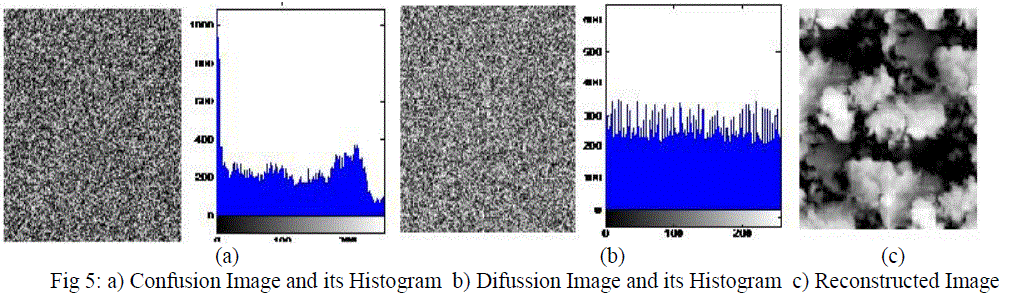
| Fig 3: Original Image and its Histogram Analysis The first stage of encryption process is pixel position confusion. The confusion process is achieved by three chaotic system, Henon, Chen and Lu. The chaotic sequence is randomly generated based on the external keystream of length 128 bit. Long keystream provides high complexity cipher image and it is unbreakable. The pixel position confusion is done by two ways, pixel by pixel or block by block approach as shown in fig. 4. Pixel by pixel approach yields a high complex encryption image than the block by block approach. But the encryption speed is good for block by block approach. The encrypted image after confusion process is highly correlated with the original image. Hence an additional process called diffusion is needed to provide high complex cipher image, such that the resultant image is uncorrelated with the original one. |
| The histogram analysis of confused image and diffused image as show in fig. 5. The decryption process is reverse of encryption process, the final encrypted image is first diffused with generated chaotic sequence and the resultant image is confused to get the reconstructed original image. The two stages of encryption process makes original image unpredictable. The method is also employed for grayscale, colour and monochrome images. The attractive features of chaotic systems are more suitable for real time communication. For real time communications, delay is most important parameter. Delay is directly related to number of iterations involved in encryption stages. If the number of iterations is minimum, the encryption delay is reduced. Hence block by block approach is usually preferred for real time communications. |
 |
 |
IV. SECURITY ANALYSIS |
| The strength of the proposed image encryption chaotic scheme is analyzed with various security tests. Key space analysis test and encryption time analysis was carried out to prove the efficiency of the proposed work. For a high complex image encryption, the key stream should be large enough to make impossible for brute force attack. |
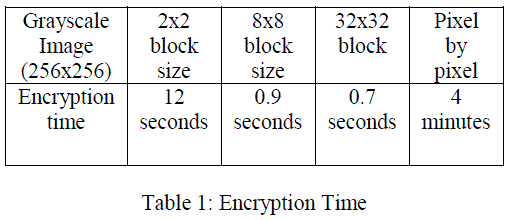
| A 16 byte (128 bit) key is used to for confusion and diffusion process of image pixel. The encryption time should not be large enough for real time application. It has been stated that the encryption time is greatly affected by pixel by pixel approach and reduced for block-by-block approach. Greater the block size, will yield greater reduction in encryption time as shown in table. 1. But there is a trade-off between the block size and security. When the block size increases, the encryption time increases but the level of security is reduced. Therefore an optimal block size is preferred for image encryption. Hence block by block approach is well suited for real time communications. |
 |
V. CONCLUSION |
| The proposed model has unique and stronger approach of image encryption. The pixel and block approaches are comparatively progressive and encrypted with 128 bit external key stream. The performance analysis and evaluation results shows that the proposed system can withstand without forfeiting the security and provides realistic solution for privacy. The way in which the keys get assigned to each frame is also performed by another chaotic map whose values cannot be predicted in the longrun. Brute force attacks and differential attacks are made unfeasible. The proposed method promises substantial security, a prime requirement for many multimedia applications. The system is also forceful against histogram based attacks. |
| The future work aims towards image storage capacity or transmission, lossless or lossy compression is usually employed so as to reduce the information storage which is transmitted. |
References |
|