ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Reshma Radhakrishnan1 and A. Kalaichelvi2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Parents have a growing array of options in choosing a school, though the extent of the options varies from place to place. In this paper, the Extent Analysis Method on Fuzzy Analytic Hierarchy Process (abbreviated as Fuzzy AHP) is used to develop a decision making model for choosing the best school for the children.
Keywords |
| Fuzzy Analytic Hierarchy Process, Triangular Fuzzy numbers, Extent analysis Method, Pairwise Comparison, Fuzzy Synthetic Extent. |
INTRODUCTION |
| Decision Making is the act of choosing between two or more courses of action. Decision-making can also be regarded as a problem-solving activity terminated by a solution deemed to be satisfactory among several alternative possibilities. It is, therefore, a reasoning or emotional process which can be rational or irrational and can be based on explicit assumptions or implicit assumption. There are processes and techniques to improve decision-making and the quality of decisions. |
| Nowadays, decision making is a problem of every common man to take right decision on many routine affairs like education for children, food, transportation, purchase of durables, healthcare, shelter and so on. In this research the authors consider the problem of selecting the best school for the children. Parents have a growing array of options in choosing a school, though the extent of the options varies from place to place. Generally parents consider various factors to select the best school for their children. The researchers identified many such important factors and used the same to develop a mathematical model for decision making regarding the selection of right school for the children using Extent Analysis Method on Fuzzy Analytic Hierarchy Process. |
BASIC DEFINITIONS |
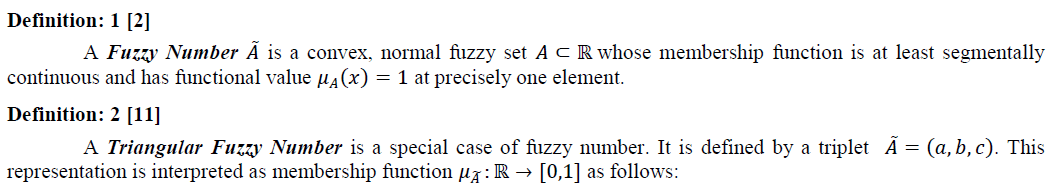 |
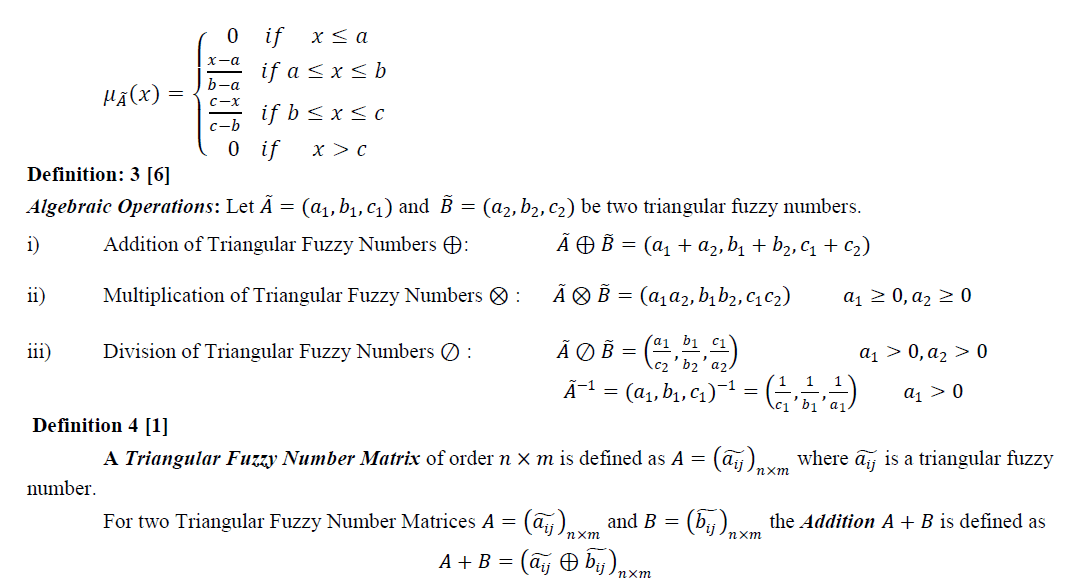 |
EXTENT ANALYSIS METHOD |
| The extent analysis method is used to consider the extent to which an object can satisfy the goal, i.e., satisfaction extent. In this method the “extent” is quantified using triangular fuzzy number. On the basis of fuzzy values for the extent analysis of each object, a fuzzy synthetic degree values can be obtained, which is defined as follows: |
 |
| Table 1. Triangular Fuzzy Conversion Scale |
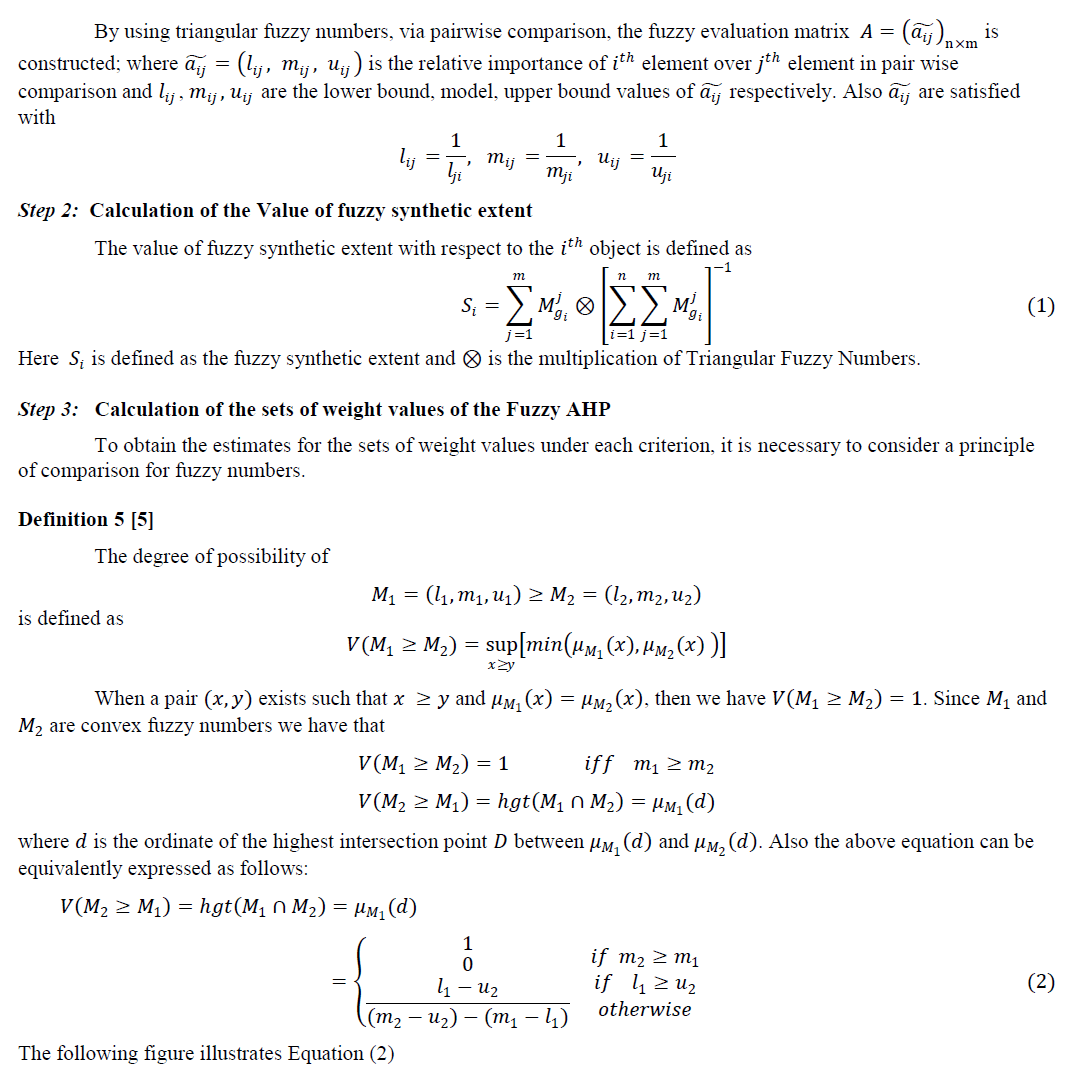 |
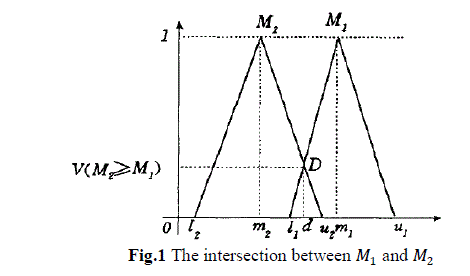 |
APPLICATION OF EXTENT ANALYSIS METHOD ON FUZZY AHP |
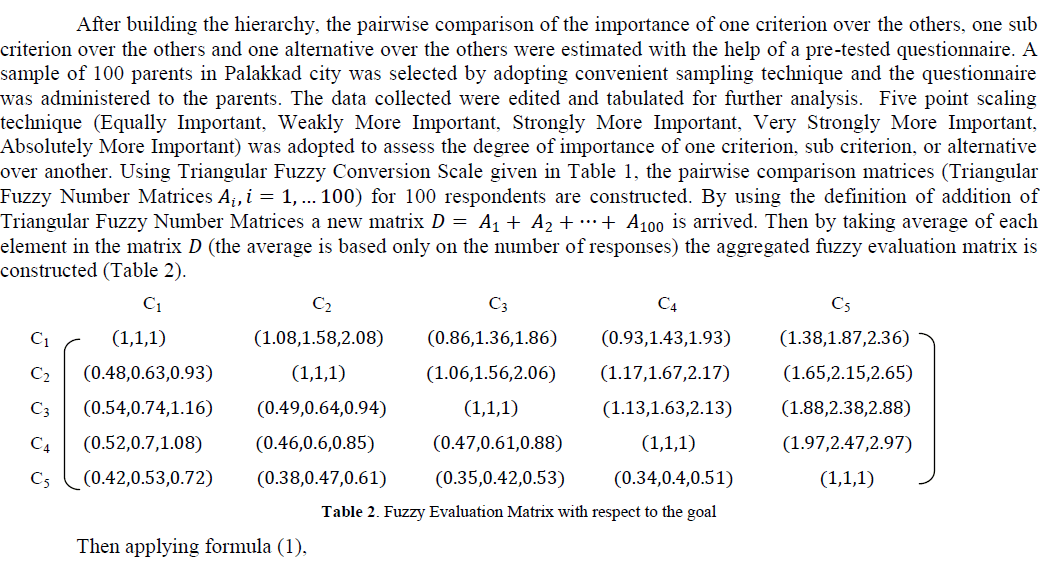
| Based on the pilot study, the researchers identified five major criteria for developing a model for the selection of the best school by the parents for their children. Further, care was taken to enlist possible sub criteria for each major criteria, which are considered by them as vital for achieving the objective. The details are presented below. |
 |
 |
| After the initial screening, three schools listed below were considered as alternatives and an attempt has been made by the researchers to develop a model to select the best one based on the above criteria. |
| 1) A1 : P.M.G HIGHER SECONDARY SCHOOL, COLLEGE ROAD, PALAKKAD |
| 2) A2 : BHARATH MATHA HIGHER SECONDARY SCHOOL, CHANDRANAGAR, PALAKKAD |
| 3) A3 : VYASA VIDYA PEETHOM SCHOOL, KALLEKAD, PALAKKAD. |
 |
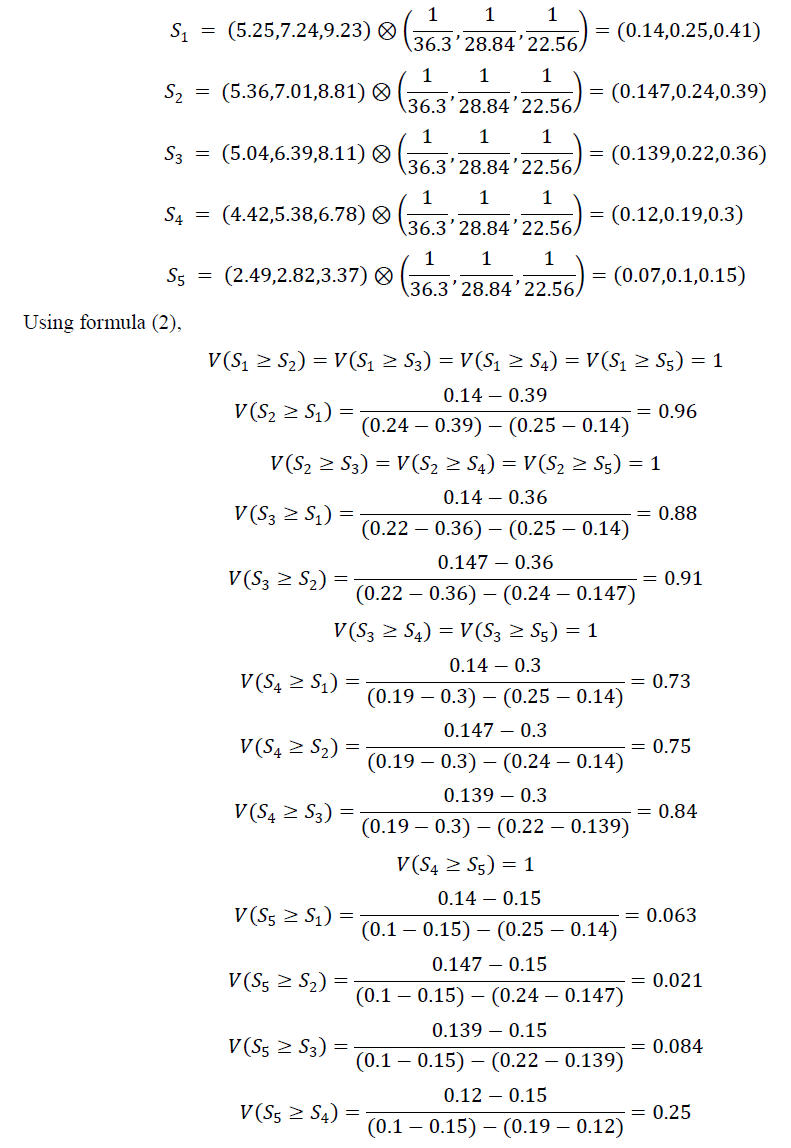 |
 |
 |
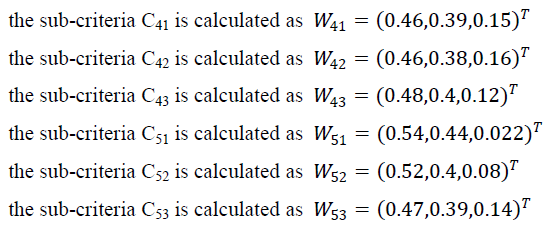 |
 |
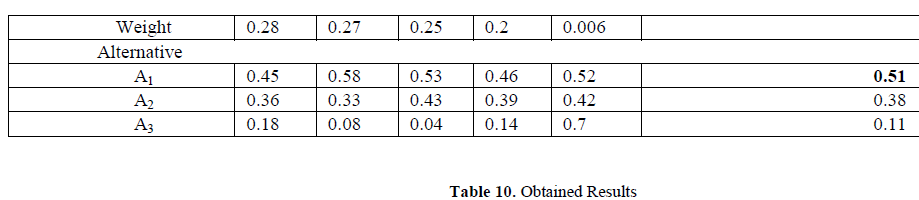 |
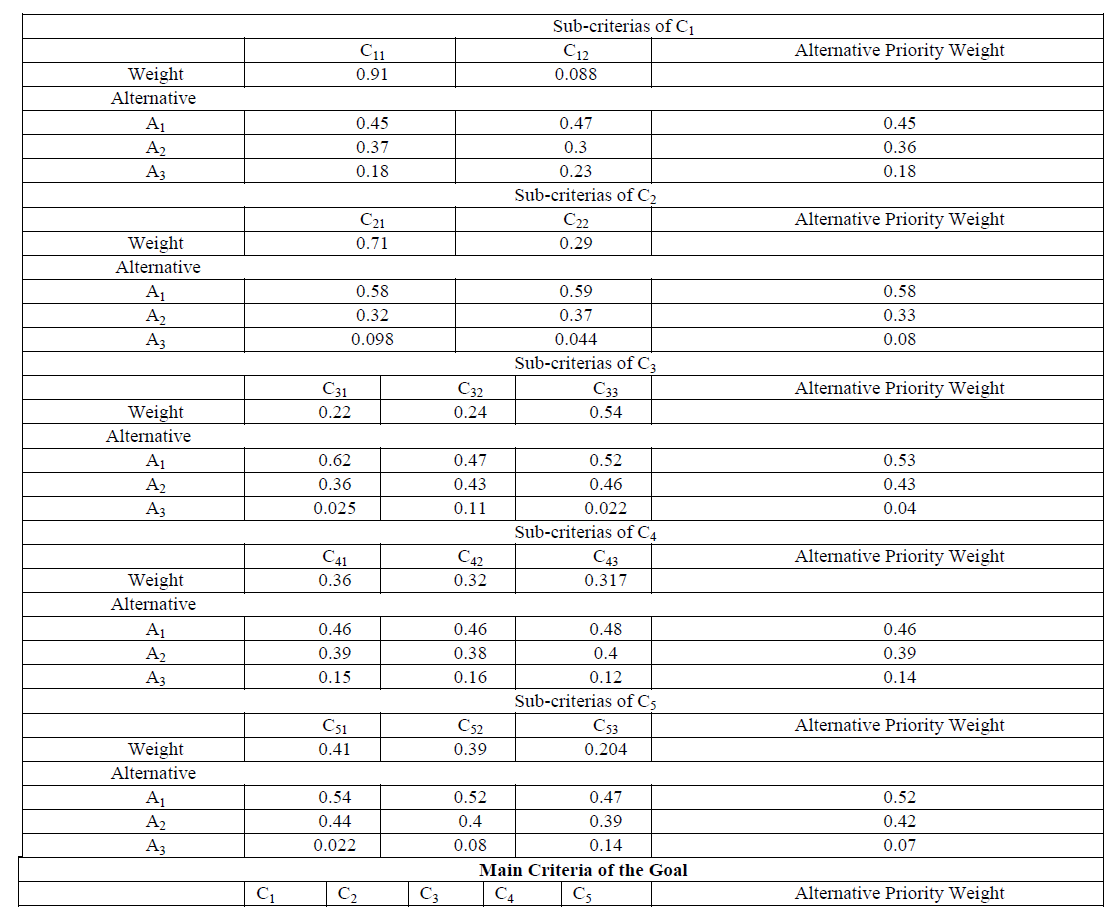
| The combination of priority weights for criteria, sub criteria and alternatives to determine the priority weight for the best school are shown in Table 10. Based on this result alternative 1(P.M.G Higher Secondary School, College Road, Palakkad) which has the highest alternative priority weight 0.51 is found to be the best school. |
CONCLUSION |
| People often find it hard to make decisions in a complex, subjective situation with more than a few realistic options. So we need a systematic, organized mathematical way to evaluate our choices and figure out which one offers the best solution to our problem. Application of the Extent Analysis Method on Fuzzy AHP in real life problems helps the people to take a correct decision from the available alternatives. |
References |
|