ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
T.Nandhini1, A.Kalaichelvi2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this paper a new class of soft sets called Soft ÄÂ-Closed sets in Soft Topological Spaces is introduced and studied. This new class is defined over an initial universe and with a fixed set of parameters. Some basic properties of this new class of soft sets are investigated. This new class of Soft ÄÂ-Closed sets contributes to widening the scope of Soft Topological Spaces and its applications.
Keywords |
| Soft Sets, Soft Topological Spaces, g-closed sets, ÃâÃÂ-closed sets, Soft g-closed sets, Soft ÃâÃÂ-closed sets |
I. INTRODUCTION |
| Any Research work should result in addition to the existing knowledge of a particular concept. Such an effort not only widens the scope of the concept but also encourages others to explore new and newer ideas. Here the researchers have succeeded in their knowledge building effort by introducing a new class of soft sets called Soft ÃâàClosed sets in Soft Topological Spaces. |
| Molodtsov (1999) initiated the theory of soft sets as a new mathematical tool for dealing uncertainty, which is completely a new approach for modeling vagueness and uncertainties. Soft Set Theory has a rich potential for application in solving practical problems in Economics, Social Sciences, Medical Sciences etc. Applications of Soft Set Theory in other disciplines and in real life problems are now catching momentum. Molodtsov successfully applied Soft Theory into several directions, such as Smoothness of Functions, Game theory, Operations Research, Riemann Integration, Perron Integration, Theory of Probability, Theory of Measurement and so on. Maji et al. (2002) gave first practical application of Soft Sets in decision making problems. Shabir and Naz(2011) introduce the notion of soft topological spaces which are defined over an initial universe with a fixed set of parameters. They studied some basic concepts of soft topological spaces also some related concepts such as soft interior, soft closure, soft subspace and soft separation axioms. In this paper a new class of sets called Soft ÃâÃÂ-Closed sets are introduced and few of their properties are investigated. |
II. RELATED WORK |
| Some concepts in mathematics can be considered as mathematical tool for dealing with uncertainties namely theory of vague sets, theory of rough sets and etc. But all of these theories have their all difficulties. The concept of soft set now introduce by Molodtsov[13] in 1999 as a general mathematical tool for modeling uncertainty present in real life. Later on Maji et al [11] proposed several operations on soft sets and some basic properties and then Pei and Miao investigated the relationships between soft sets and information systems. Shabir and Naz [16] introduced the notion of soft topological spaces which are defined over an initial universe with a fixed set of parameters. Latter on Veerakumar [18] defined ÃâÃÂclosed sets and deeply studied on ÃâÃÂ-locally closed sets and GLC-functions and also study many basic properties of ÃâÃÂ-closed sets together with the relationships of these sets with some other sets. |
III. PRELIMINARIES |
| Let X be an initial universe set and E be the set of parameters. Let P(X) denote the power set of X. For a Soft set (F, E) a space (X, τ, E), Cl(F, E), Int(F, E), spInt(F, E), spCl(F, E), ssInt(F, E), and ssCl(F,E) denote the soft closure of (F, E), soft interior of (F,E), soft pre interior of (F, E),soft pre closure of (F, E), soft semi interior of (F, E) and soft semi closure of (F, E) respectively. |
Definition 2.1[13] |
| For A ⊆ E, the pair (F,A) is called a Soft Set over X, where F is a mapping given by F:A → P(X). |
| In other words, a soft set over X is a parameterized family of subsets of the universe X. For ε ∈ A, F(ε) may be considered as the set of ε- approximate elements of the soft set (F,A). |
Definition 2.2 [14] |
| A soft set (F,A) over X is said to be Null Soft Set denoted by Φ if for all e ∈ A, F(e) = φ. A soft set (F, E) over X is said to be an Absolute Soft Set denoted by A if for all e ∈ A, F(e) = X. |
Definition 2.3 [11] |
| The Union of two soft sets (F,A) and (G, B) over X is the soft set (H, C), where C = A ∪ B, and for all e ∈ C, H(e) = F(e), if e ∈ A\B, H(e) = G(e) if e ∈ B\A and H(e) = F(e) ∪ G(e) if e ∈ A ∩ B and is denoted as (F,A) ∪ (G, B) = (H, C). |
Definition 2.4 [11] |
| The Intersection of two soft sets (F,A) and (G, B) over X is the soft set(H, C), where C = A ∩ B and H(e) = F(e) ∩ G(e) for all e ∈ C and is denoted as (F,A) ∩ (G, B) = (H, C). |
Definition 2.5 [14] |
| The Relative Complement of (F,A) is denoted by (F,A)C and is defined by (F,A)C = (FC,A) where FC:A → P(X) is a mapping given by FC(e) = X − F(e) for all e ∈ A. |
Definition 2.6 [14] |
| The Difference (H, E) of two soft sets (F, E) and (G, E) over X, denoted by (F, E)\(G,E) is defined as H(e) = F(e)\G(e) for all e ∈ E. |
Definition 2.7 [14] |
| Let (F,A) and (G, B) be soft sets over X, we say that (F,A) is a Soft Subset of (G, B) if A ⊆ B and for all e ∈ A, F(e)and G(e) are identical approximations. We write (F,A) ⊆ (G, B). |
Definition 2.8[14] |
| Let τ be a collection of soft sets over X with the fixed set E of parameters. Then τ is called a Soft Topology on X if |
 |
| The members of τ are called Soft Open sets in X and complements of them are called Soft Closed sets in X. |
Definition 2.9 [8] |
| Let (X, τ, E) be a Soft Topological Spaces over X. The Soft Interior of (F, E) denoted by Int(F, E) is the union of all soft open subsets of (F,E). Clearly (F, E) is the largest soft open set over X which is contained in (F, E). The Soft Closure of (F, E) denoted by Cl(F, E) is the intersection of closed sets containing(F,E). Clearly (F, E) is the smallest soft closed set containing(F, E). |
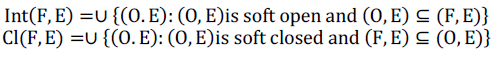 |
Result 2.10 [14] |
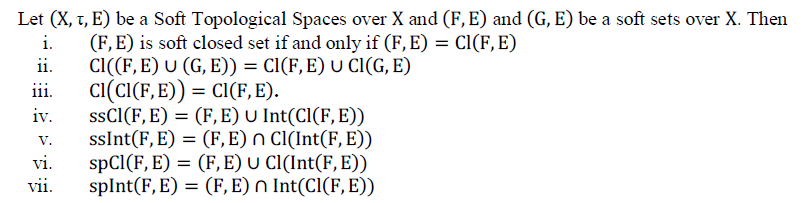 |
 |
 |
IV. SOFT ÃâÃÂ-CLOSED SETS IN SOFT TOPOLOGICAL SPACES |
Definition 3.1 |
 |
 |
V. CONCLUSION |
| In the present work, a new class of sets called Soft ÃâÃÂ-Closed sets in Soft Topological Spaces is introduced and some of their properties are studied. This new class of sets widens the scope to do further research in the areas like Bitopological Spaces, Smooth topological Spaces and Fuzzy Soft Topological Spaces. |
References |
|