ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Preeth.R,Shivakumar.N,Balaji.N
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Software effort estimation is one of the most challenging and important activity in software development. Accurate estimates not only help the customer make successful investments but also assist the software project manager in coming up with appropriate plans.Research on software effort estimation is needed to build more accurate models of the key aspects of software development.The exact relationship between the attributes of the effort estimation are difficult to establish.Int his dissertation,an extension to the well known model for effort estimation,COCOMOII,is introduced for improving the effort estimation accuracy of software maintainence.The existing techniques cannot handle the dataset having categorical variables efficiently including the analogy method The performance of this proposed methodology illustrates that there is arealistic validationof the results with the realtime NASA dataset.The results were analyzed using the Mean Magnitude Relative Error(MMRE) to prove its efficiency.
RELATED WORK |
| Uncertainty at the early stage is a pervasive problem in software effort estimation as the available data is often imprecise and vague. Generally, uncertainty in software measurement is associated with lack of precise knowledge such that software developers sometimes have measurements that are inaccurate, inexact or of low confidence. For example “Software testing might need 10 man-months”, which exhibits a degree of imprecision [1]. Moreover, there is no estimation model that can include all the factors that affect the effort required to complete a software project [2]. [3] Proposed an early stage software effort estimation method based on Grey Relational Analysis (GRA) called GRACE. They employed GRA to select an optimal attribute set based on the similarity degree between dependent attribute and other variables. The variables are preferably continuous rather than categorical. The GRA is later used to derive new estimates by finding the closest case that approximately agrees with the current case on all effort drivers. Recently [4], developed a new similarity measure based on integration of Fuzzy set theory and Grey Relational Analysis for analogy-based estimation. The proposed measure has the capability to deal with numerical and categorical attributes such that two levels of similarity measure have been defined: local and global measures. The results obtained suggested that the proposed model produces good accuracy when compared to other well-known estimation techniques such as case-based reasoning, stepwise regression and artificial neural network. [5] Proposed a new Fuzzy analogy software cost estimation based on linguistic quantifiers. The model was designed for the datasets that are described by linguistic quantifiers (using an ordinal scale). |
PROPOSED ALGORITHM |
| The Fig 1 adaptive neuro-fuzzy model for software development effort estimation is capable of learning ability and good interpretability. Artificial neural networks have a massive parallel structure in the form of a directed graph, composed of processing units (neurons) that are linked through connections. The input for this model is the ratings of 6 grouped attributes. Each attribute represents one factor that contributes to the development effort, such as application domain experience, product complexity and etc. This model integrates both neural networks and fuzzylogic principles, it has potential to capture the benefits of both in a single framework. Its inference system corresponds to a set of fuzzy IF–THEN rules that have learning capability to approximate nonlinear functions. |
IV. VALIDATION OF ANFIS MODEL |
| Anfis uses a hybrid learning algorithm to identify parameters of fuzzy inference systems. It applies a combination of the least-squares method and the back propagation gradient descent method for training FIS membership function parameters to emulate a given training data set. Anfis can also be invoked using an optional argument for model validation. The type of model validation that takes place with this option is a checking for model over fitting, and the argument is a data set called the checking data set |
V. EXPLORING WITH INDUSTRY DATASET |
| I have considered 93 instances of NASA93 project data with 17 attributes considering area of domain as one of the dominating factor for training my network so that a fuzzy inference system is being developed. The COCOMO cost estimation model is used by thousands of software project managers, and is based on a study of hundreds of software projects. Unlike other cost estimation models, COCOMO is an open model. COCOMO estimates are more objective and repeatable than estimates made by methods relying on proprietary models. Then, this fuzzy rule has been used for testing the input data and consequently the effort estimation is also calculated. The COCOMOII model contains only 15 effort multipliers, yet neuro fuzzy COCOMO model is completely compatible with the COCOMO II model. The actual effort in the COCOMO dataset is measured in person-months which represents the number of months that one person would need to develop a given project. Despite then the fact that the COCOMO datasets are now over 25 years old, it is still commonly used to assess the comparative accuracy of new techniques. |
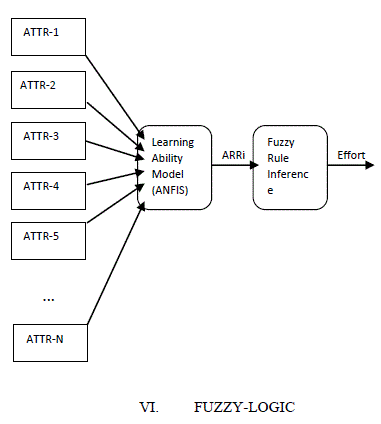 |
FUZZY-LOGIC |
| Fuzzy logic is used to find fuzzy numbers and then the result is defuzzified to get the rate factor and hence the size estimation in person hours. Triangular fuzzy numbers are used to represent the linguistic terms in neuro fuzzy complexity matrixes. A fuzzy set is characterized by a membership function, which associates with each point in the fuzzy set a real number in the interval [0, 1], called degree or grade of membership. The membership function may be triangular, trapezoidal, parabolic erection. A triangular fuzzy number (TFN) is described by a triplet (α ,m, β), where m is the modal value, α and β are the right and left boundary respectively. We take each linguistic variables as a triangular Fuzzy numbers, TFN (α, m, β), α ≤ m, β ≥ m. The membership function (μ(x)) for which is defined as: |
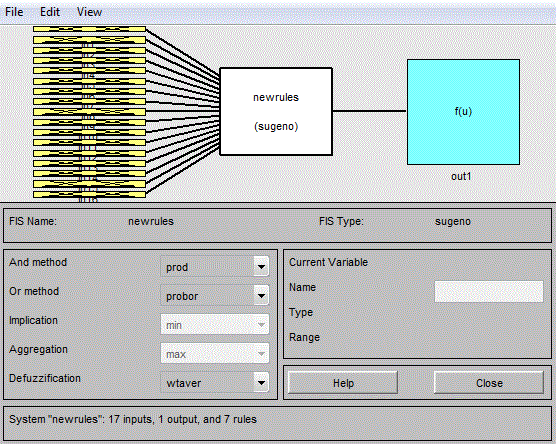
| Fuzzy rule Inference: Fuzzy inference is the process of formulating the mapping from a given input to an output using fuzzy logic. Information flows from left to right, from seventeen inputs to a single output. The parallel nature of the rules is one of the more important aspects of fuzzy logic systems. Instead of sharp switching between modes based on breakpoints, logic flows smoothly from regions where the |
 |
VII. DEFUZZIFICATION |
| `Defuzzification means the fuzzy to crisp conversions. The fuzzy results generated cannot be used as such to the hence it is necessary to convert the fuzzy quantities into crisp quantities for further processing. This can be achieved by using defuzzification process. The defuzzification has the capability to reduce a fuzzy to a crisp single-valued quantity or as a set, or converting to the form in which fuzzy quantity is present. Defuzzification can also be called as “rounding off” method. Defuzzification reduces the collection of membership function values in to a single sealer quantity. Defuzzification is the process of producing a quantifiable result in fuzzy logic, given fuzzy sets and corresponding membership degrees. It will have a number of rules that transform a number of variables into a fuzzy result, that is, the result is described in terms of membership in fuzzy sets. Data defuzzification is constructed based on a rule induction system replacing the crisp facts with fuzzy inputs then an interference engine uses a base of rules to map inputs to a fuzzy output which can be a crisp value or left as a fuzzy value. |
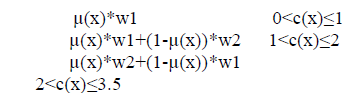 |
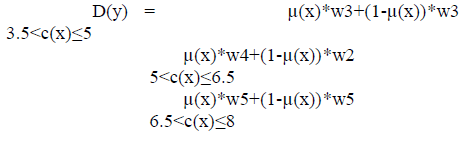 |
VIII. VARIOUS CRITERIONS FOR ASSESSMENT OF SOFTWARE COST ESTIMATION MODELS |
| 1. Mean Magnitude Relative Error (MRE), computes the absolute percentage of error between actual and predicted effort for each reference project MRE=|actuali-Estimatedi| /actuali . 2. Mean Magnitude Relative Error (MMRE), calculates the average of MRE over all referenced projects MMRE=1/n ΣMREi. |
| 3Pred (l), is used as a complementary criterion to count the percentage of estimates that fall within less than or equal to l of the actual values. Pred(l)=α/N*100. |
IX. EXPERIMENTAL RESULTS |
| Performance of the effort can be predicted based on the MARE and Prediction n method. The estimated effort of LOC is compared with the actual effort of LOC in the first graph. The estimated |
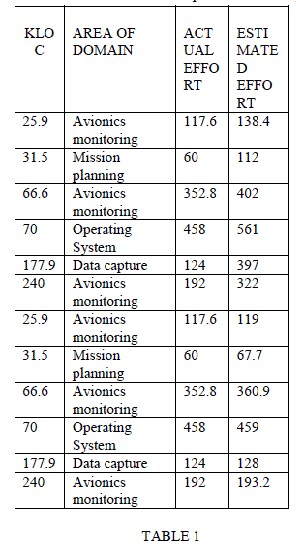 |
| effort of neuro model is compared with the actual effort of COCOMO in the second graph. The MARE of LOC and neuro model is compared in the third graph. It has been clearly identified that Function point based estimation is better than the LOC estimation. The Table 1 indicates the kilo lines of code and its corresponding domain with its actual effort and the estimated effort using the cocomo model. Both MARE analysis and Prediction n method has been applied to the direct approach and the nonalgorthmic approach. The actual effort is the original effort and the estimated effort is the one which has been done in the estimation process using the COCOMO method. The below given graph shows the comparison of the actual effort and estimated neuro-fuzzy effort for 93 instances such that the deviation is so mere to show the accuracy rate of our estimated model. |
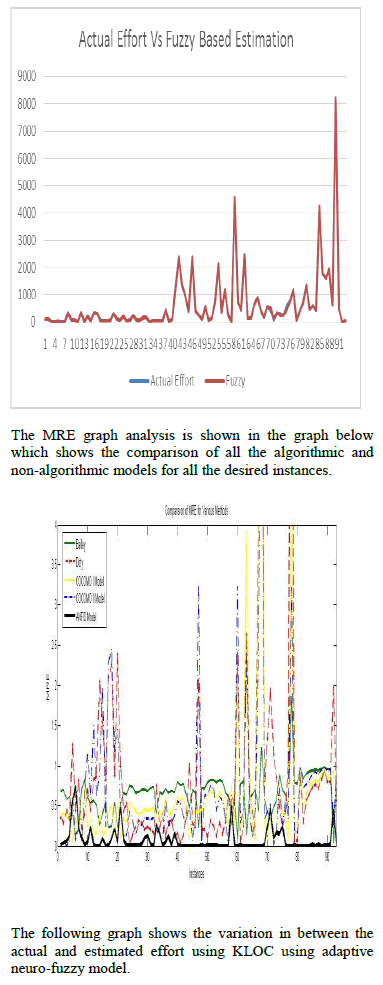 |
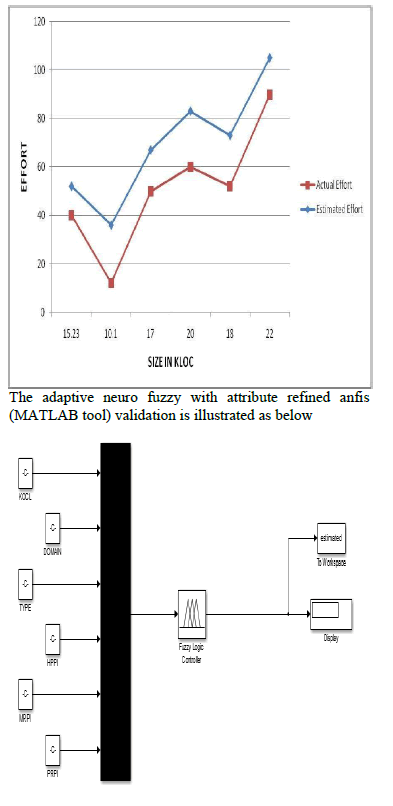 |
X. CONCLUSION AND FUTURE WORK |
| `This project proposes an efficient way of estimating the effort. The results of the estimation based on the direct method shows that the deviation between the actual and the estimated effort is more. The result of nonalgorithmic method using the adaptive neuro technique based estimation reduces the relative error and the mean absolute relative error. So the analysis of the effort from direct method and nonalgorthmic method gives that adaptive neuro fuzzy based estimation is the efficient method for the estimation process. |
| Though COCOMO model which is algorithmic method is an open model. It has some limitations also. In the ANFIS based estimation also exists the deviation between actual and estimated effort. So the same effort can be implemented by using other non-algorithmic Method. In future this non algorithmic like Machine learning, Neuro fuzzy based multilayer feed forward network estimation can be done to achieve the better performance.This fuzzy based estimation using the Triangular Membership Function has been proposed in this paper. In future this non algorithmic based estimation can be enhanced by refining the attributes in training the network model, which invariantly helps to achieve the better performance. |
References |
|